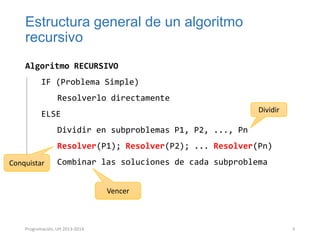
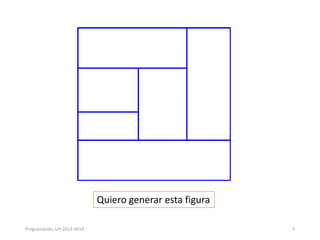
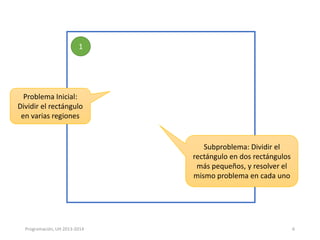
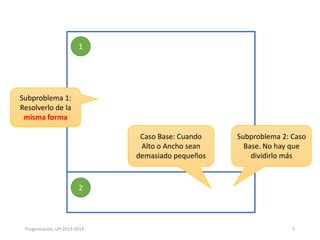
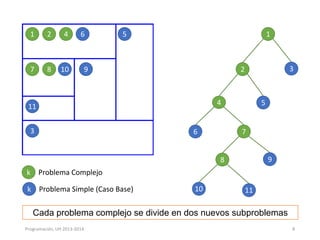
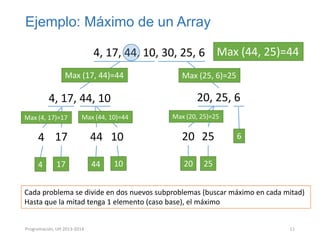
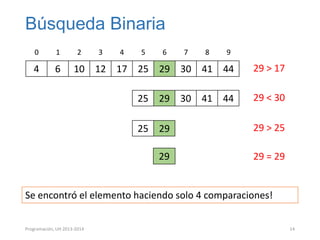
Este documento presenta los conceptos de recursividad y algoritmos recursivos. Explica que la recursividad implica dividir un problema complejo en subproblemas más simples, resolver los subproblemas de forma recursiva y luego combinar las soluciones para resolver el problema original. Incluye ejemplos como dividir un rectángulo recursivamente, encontrar el máximo de un arreglo de forma recursiva y ordenar un arreglo mediante el método de mezcla recursivo. El documento concluye con ejercicios prácticos sobre temas como búsqueda binaria, ordenación quick

1. Recursividad
Divide y Vencerás
Programación
Lester Sánchez
Universidad de La Habana
2013 – 2014

2. Divide y Vencerás
1. Dividir el problema complejo en subproblemas
simples
2. Conquistar (resolver) los problemas simples
3. Vencer (resolver) el problema original a partir de
las soluciones de los problemas simples
Programación, UH 2013-2014
2

3. Estructura general de un algoritmo
recursivo
Algoritmo RECURSIVO
IF (Problema Simple)
Resolverlo directamente
Dividir
ELSE
Dividir en subproblemas P1, P2, ..., Pn
Resolver(P1); Resolver(P2); ... Resolver(Pn)
Conquistar
Combinar las soluciones de cada subproblema
Vencer
Programación, UH 2013-2014
3

4. Composition with Large Red Plane, Yellow, Black, Gray and Blue
Piet Mondrian, 1921

5. Quiero generar esta figura
Programación, UH 2013-2014
5

6. 1
Problema Inicial:
Dividir el rectángulo
en varias regiones
Subproblema: Dividir el
rectángulo en dos rectángulos
más pequeños, y resolver el
mismo problema en cada uno
Programación, UH 2013-2014
6

7. 1
Subproblema 1:
Resolverlo de la
misma forma
Caso Base: Cuando
Alto o Ancho sean
demasiado pequeños
Subproblema 2: Caso
Base. No hay que
dividirlo más
2
Programación, UH 2013-2014
7

8. 1
2
4
7
8
6
10
5
1
9
4
11
3
3
2
6
5
7
9
8
k Problema Complejo
k Problema Simple (Caso Base)
10
11
Cada problema complejo se divide en dos nuevos subproblemas
Programación, UH 2013-2014
8

9. Ejemplo: Mondrian
Dividir los dos
nuevos rectángulos
que se forman
Obtener
punto de
división
Dividir los dos
nuevos rectángulos
que se forman
Dibujar
línea
divisoria
Programación, UH 2013-2014
9

10. DEMO
Mondrian
Programación, UH 2013-2014
10

11. Ejemplo: Máximo de un Array
4, 17, 44, 10, 30, 25, 6 Max (44, 25)=44
Max (17, 44)=44
Max (25, 6)=25
20, 25, 6
4, 17, 44, 10
Max (4, 17)=17
Max (44, 10)=44
4 17
4
17
44 10
44
10
Max (20, 25)=25
20 25
20
6
25
Cada problema se divide en dos nuevos subproblemas (buscar máximo en cada mitad)
Hasta que la mitad tenga 1 elemento (caso base), el máximo
Programación, UH 2013-2014
11

12. Ejemplo: Máximo de un Array
El método público
se limita a invocar
al recursivo con los
parámetros iniciales
Método Recursivo.
Recibe índices para
limitar el rango
donde buscar
Si hay un único
elemento, es el máximo
Programación, UH 2013-2014
El máximo del array es el
máximo de los máximos
de cada mitad
12

13. Búsqueda Binaria
Ejemplos de la vida cotidiana
‐ Buscar una palabra en un diccionario
‐ Buscar un nombre en el directorio telefónico
‐ Buscar una página de un libro
‐ Retomar la visualización de un video
En general optimizamos la búsqueda cuando los
elementos están ordenados
Optimización en este caso significa hacer menos comparaciones para
encontrar el elemento… o determinar que no está
Programación, UH 2013-2014
13

14. Búsqueda Binaria
0
1
4
6
2
3
4
5
6
7
8
9
10 12 17 25 29 30 41 44
29 > 17
25 29 30 41 44
29 < 30
25 29
29 > 25
29
29 = 29
Se encontró el elemento haciendo solo 4 comparaciones!
Programación, UH 2013-2014
14

15. Búsqueda Binaria
0
1
4
6
2
3
4
5
6
7
8
9
10 12 17 25 29 30 41 44
28 > 17
25 29 30 41 44
28 < 30
25 29
28 > 25
29
28 != 29
Se determinó que el elemento no está haciendo solo 4 comparaciones!
Programación, UH 2013-2014
15

16. Búsqueda Binaria
1
2
3
4
5
6
7
8
…
n
n/2
(n/2)/2 = n/4 = n/22
((n/2)/2)/2 = n/8 = n/23
.
.
.
Cantidad de elementos
del nuevo fragmento
Cuando n/2k = 1 no hay
nada más que dividir
(((n/2)/2)/2) … /2 = n/2k
k es la cantidad
máxima de divisiones
Programación, UH 2013-2014
16

17. Búsqueda Binaria
O sale por aquí
Buscar en la 2da mitad
Buscar en la 1ra mitad
O sale por aquí
Programación, UH 2013-2014
17

18. Ordenación por Mezcla (Merge
Sort)
Si se tienen dos arrays ordenados, se pueden mezclar
de forma tal que el array resutante siga ordenado
ALGORITMO RECURSIVO
1. Dividir el array en dos mitades
2. Ordenar cada mitad de la misma forma
3. Mezclar las dos mitades
4. Una mitad de 1 elemento está ordenada
Programación, UH 2013-2014
18

19. Ejemplo: Ordenación por Mezcla
38
38
43
3
43
27
27
38
27
43
27
38
27
3
43
38
10
82
38
10
82
9
27
10
82
9
43
9
10
82
9
3
27
82
9
3
3
Programación, UH 2013-2014
9
9
43
38
3
3
10
43
82
82
19

20. Ordenación por Mezcla
Se utiliza para
hacer la mezcla
Si el fragmento tiene un solo
elemento, está ordenado!
Ordenar la 1ra mitad
Ordenar la 2da mitad
Mezclar las dos
mitades ordenadas
Programación, UH 2013-2014
20

21. Ordenación por Mezcla
Copiar los restantes
de la 1ra mitad
Copiar los restantes
de la 2da mitad
Copiar el fragmento
ordenado al array original
Programación, UH 2013-2014
21

22. Clase Práctica
Implementar la búsqueda en un array desordenado
int Buscar (int[] a, int n)
Determinar cantidad mínima de inserciones requeridas para
convertir una cadena en palíndromo
Ejemplo: A la cadena “abcb” basta con insertarle una “a” por
detrás para convertirla en palíndromo (abcba) y a “abecba”
basta con insertarle una “e” en el medio (abeceba) o una “c”
(abcecba).
int InsercionesPalindromo(string s)
Programación, UH 2013-2014
22

23. Clase Práctica
Implemente el algoritmo de ordenación QuickSort.
void QuickSort(int[] a)
El QuickSort se basa en la idea de reorganizar los elementos
de un array, seleccionando un elemento (pivote) y colocando
todos los menores que él al inicio del array y los mayores e
iguales al final. Implemente esta estrategia en un algortimo
recursivo utilizando la técnica de divide y vencerás.
Programación, UH 2013-2014
23

24. Clase Práctica
Un TAXISTA se desplaza por una ciudad en la que solo está
permitido conducir hacia el ESTE y hacia el SUR. Calcule la
cantidad de caminos desde un origen hasta un destino.
int CantidadCaminos(int xOrig, int yOrig, int
xDest, int yDest)
Calcule la cantidad de cadenas balanceadas que pueden
formarse con n pares de paréntesis.
int CadenasBalanceadas(int n)
Programación, UH 2013-2014
24

25. Clase Práctica
Implemente un método que imprima en la Consola la
descomposición en sumandos de un número n.
Ejemplo: n = 5
1+1+1+1+1
1+1+1+2
1+2+2
1+1+3
1+4
2+3
5
void DescomposicionSumandos(int n)
Programación, UH 2013-2014
25