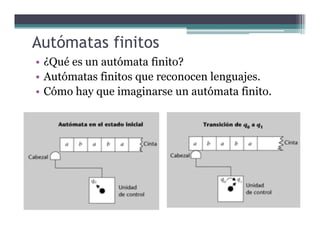
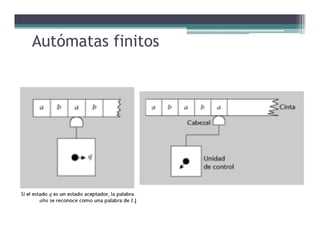
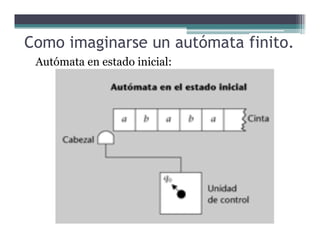
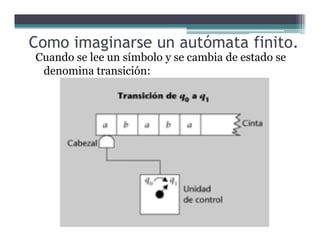
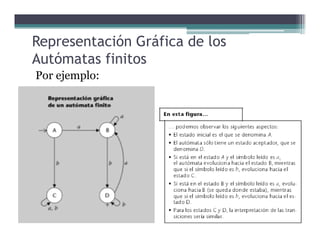
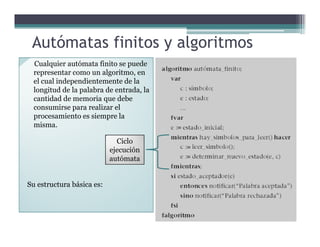
Este documento presenta conceptos básicos sobre conjuntos, palabras, lenguajes y autómatas finitos. Explica definiciones clave como alfabeto, palabra, lenguaje, subpalabras, prefijos y sufijos. También describe operaciones sobre palabras y lenguajes como concatenación, inversión, clausura de Kleene y cierre positivo de Kleene. Finalmente, introduce brevemente el concepto de autómata finito y cómo estos reconocen lenguajes.