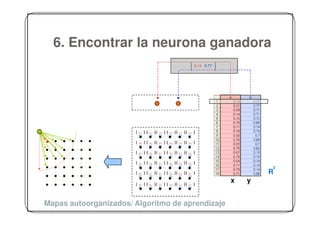
Este documento describe los conceptos fundamentales de las redes neuronales competitivas y los mapas autoorganizados de Kohonen. Explica cómo estas redes se inspiran en procesos biológicos como la autoorganización neuronal y cómo aprenden mediante competición entre neuronas para clasificar datos de entrada de forma no supervisada. Finalmente, detalla los pasos para crear un modelo de mapa autoorganizado, incluyendo la inicialización de pesos y la determinación de la topología y el tamaño de la red.

1. Aula: Redes Competitivas y
Mapas de Kohonen

2. Antecedentes
Los trabajos de Von der Malsburg (1973) trazan la
auto organización de las células nerviosas.
En 1975, Fukushima propuso el cognitron que es
una red competitiva multicapa y auto organizada.
Willshaw y von der Malsburg (1976) trabajaron
sobre la formación de las conexiones neuronales
mediante Autoorganización.
Grossberg (1972, 1976) sobre la clasificación
adaptativa de patrones.
2

3. Aprendizaje supervisado
Se le suministra a la red un conjunto de datos de entrada y la
respuesta esperada.
Se comparan los datos obtenidos por el sistema con los datos
de entrada aportados, con la respuesta esperada y se
modifican los pesos en función del error obtenido.
El conjunto de datos utilizados en el proceso de aprendizaje
se denomina conjunto de entrenamiento (training set).
Si los vectores de entrada utilizados no contienen la
información idónea la red puede llegar a no aprender.
Mecanismos de aprendizaje

4. Aprendizaje no supervisado
Sólo se aplica a la red neuronal los datos de entrada, sin indicarle
la salida esperada.
La red neuronal es capaz de reconocer algún tipo de estructura
en el conjunto de datos de entrada (normalmente redundancia de
datos) y de esta forma se produce auto-aprendizaje.
Durante el proceso de aprendizaje la red autoorganizada debe
descubrir por sí misma rasgos comunes, regularidades,
correlaciones o categorías en los datos de entrada, incorporarlos
a su estructura interna de conexiones.
Se dice, por tanto, que las neuronas deben auto-organizarse en
función de los estímulos (datos) procedentes del exterior.
Mecanismos de aprendizaje

5. Neurociencias Conceptos
La inspiración biológica

6. Humunculus, el hombrecito dentro del cerebro
La inspiración biológica

7. Humunculus, el hombrecito dentro del cerebro
La inspiración biológica

8. Cartas retinotópicas
Hubel & Wiesel
La inspiración biológica

9. Cartas retinotópicas

10. Informaciones Multidimensionales
La inspiración biológica

11. Sinestesia
La inspiración biológica

12. Sinestesia
La inspiración biológica

13. Proceso biológico
Si algunas regiones del espacio de entrada son mas usadas que otras y
reciben una rica variedad de estímulos estas se mapearan mejor.
(ej. Las manos de un pianista o un cirujano)

14. Autoorganización
Cada nodo de la red tiene
conexiones exicitatorias laterales
con su vecinos mas próximos pero
conexiones laterales inhibitorias con
sus vecinos mas distantes.
En el mapa topográfico cortical estas
regiones crecerán , mientras que las
regiones que no son usadas se
harán mas pequeñas.
La inspiración biológica

15. El “sombrero mejicano”
Respuesta Positiva
+ (Excitación)
- Respuesta Negativa
(Inhibición)
La inspiración biológica

16. El “sombrero mejicano”
La inspiración biológica

17. Biológico
Tomando la inspiración biológica
Ejemplos Red de Neuronas Mapas Autoorganizados
Estímulos del espacio Proceso de aprendizaje Al final del aprendizaje
de entrada por competición neuronas con
características
Bioinspirado
similares se ubican cerca
unas
de otras.
La inspiración biológica

18. Redes No Supervisadas
Redes Competitivas.
Mapas de Kohonen-Self Organizing Maps (SOM).
“Generación de una taxonomía de datos sin
conocimientos previos”

19. Redes Neuronales Competitivas
La competición entre neuronas hará que una sola de ellas (ó
algunas en ciertos casos) sean las que aprendan.
De esta forma lograremos que cada unidad aprenda información
diferente, es decir se especialice.

20. Red neuronal competitiva
Una red competitiva está constituida por N sensores de
entrada, M unidades de proceso (neuronas artificiales), y
conexiones entre cada sensor y cada unidad de proceso,
de manera que la conexión entre el sensor j y la unidad
de proceso i tiene asociado un valor wij.

21. Regla de aprendizaje
Por lo tanto la regla de aprendizaje es la
siguiente:
Donde r es la unidad ganadora, del mayor
potencial sinaptico:

22. Interpretación Geométrica
Para entender mejor dicha regla de aprendizaje vamos a
realizar la siguiente interpretación geométrica.

23. Aplicaciones de sistemas
organizados
“Clustering” ó agrupamiento.
Reducción de la dimensionalidad.
Detección de familiaridad (similitud entre un
valor nuevo y valores ya presentados).

24. Agrupamiento
Conjunto de datos representados en dos
dimensiones.

25. Creando el modelo bioinspirado
Inspirándose en estos comportamientos biológicos se
desarrollaron los mapas autoorganizados.
Los Mapas Autoorganizados o SOM (Self-Organizing
Maps) fueron creados por Teuvo Kohonen entre los
años 1982 y 1990
La idea se basa en un funcionamiento biológico de
aprendizaje por competición, de forma que cuando un
conjunto de datos de entrada se presenta a la red, los
pesos de las neuronas se adaptan de forma que la
clasificación presente en el espacio de entrada se
preserva en la salida.

26. Red SOFM
Capa de entrada.
Capa de Competitiva.
Conexión entre cada entrada con todas las
neuronas.

27. SOFM (Self-organizing Feature Map)
También llamados Mapas Autorganizado de
Kohonen.

28. Aprendizaje de la red Kohonen
Calculamos la mínima distancia entre los pesos
y las entradas de nuestro sistema.
Por lo tanto:

29. Aprendizaje con vecindario
Adicionamos la capacidad de relación con las
neuronas vecinas tenemos:
:valor entero que marca el
limite del vecindario de
aprendizaje

30. Tipos de Vecindarios: Bidimensionales

31. Arquitectura SOM
n Capa de entrada
… Una por cada variable de entrada
Capa de salida y competición
No existe capa oculta
n
…
m
…

32. Un ejemplo de la arquitectura SOM
Capa de entrada de tres dimensiones (x,y,z)
Capa de salida y competición de 9 neuronas

33. Capa de entrada
Tabla con ejemplos
Estímulos del espacio
de entrada.
Una neurona por cada
dimensión, en este ejemplo 3.
3
R
x y z

34. Capa de entrada
Cada neurona de la capa de
entrada esta conectada a
todas las neuronas de la
capa de salida.
3
R
x y z
Mapas autoorganizados/ Un ejemplo de la arquitectura SOM

35. Capa de entrada
18.91 22.13 27.40
Cada ejemplo es
presentado a las neuronas
de la capa de salida.
Así se buscan las neuronas
mas parecidas al vector de
entrada mediante un
proceso de competición.
Finalmente se crean
grupos con características
3 similares.
R
x y z
Mapas autoorganizados/ Un ejemplo de la arquitectura SOM

36. Capa de salida y competición
Entre las neuronas de la capa de salida, puede decirse que existen
conexiones laterales de excitación e inhibición implícitas, pues
aunque no estén conectadas, cada una de estas neuronas va a tener
cierta influencia sobre sus vecinas.
Mapas autoorganizados/ Un ejemplo de la arquitectura SOM

37. Capa de salida y competición
La influencia sobre vecinos se consigue a través de un proceso de competición
entre las neuronas y de la aplicación de una función denominada de vecindad.
2
1
Cuadrada
0
2
1
0 Hexagonal
Mapas autoorganizados/ Un ejemplo de la arquitectura SOM

38. 1.Determinar la topología del mapa

39. 2. Determinar el tamaño del mapa

40. 3. Escoger el tipo de vecindario
2 2
1 1
0 0

41. 4. Inicializar los pesos de las neuronas
2
R
x y

42. Concepto de peso
Capa de Entrada Capa de Salida
Dos w
Dimensiones Dos
w2 w1
Dimensiones
(x,y) w2
w
w1
w
Tres w3
w1 Dos
Dimensiones w w1
w2
w3 Dimensiones
(x,y,z)
w2
w
n w1
w2 Dos
Dimensiones w3
Dimensiones
…
(x,y,z, …, n) wn

43. Inicializar los pesos de las neuronas
t=0
2
R
x y

44. Inicializar los pesos de las neuronas
t=0 0.2 0.3
2
R
x y

45. Inicializar los pesos de las neuronas
0.2 0.3 0.4 0.8 0.9 0.3 0.5 0.7 0.7 0.3 0.6 0.1
0.6 0.7 0.2 0.7 0.9 0.4 0.6 0.7 0.5 0.3 0.2 0.3
0.4 0.7 0.9 0.2 0.1 0.3 0.8 0.3 0.5 0.8 0.3 0.3
t=0
0.2 0.6 0.6 0.6 0.7 0.4 0.5 0.5 0.5 0.6 0.6 0.3
0.2 0.7 0.7 0.8 0.7 0.8 0.8 0.6 0.6 0.7 0.2 0.3
0.2 0.7 0.2 0.3 0.9 0.3 0.9 0.7 0.2 0.3 0.7 0.8

46. Inicializar los pesos de las neuronas
0.2 0.4 0.9 0.5 0.7 0.6
0.3 0.8 0.3 0.7 0.3 0.1
0.6 0.2 0.9 0.6 0.5 0.2
t=0
0.7 0.7 0.4 0.7 0.3 0.3
0.4 0.9 0.1 0.8 0.5 0.3
0.7 0.2 0.3 0.3 0.8 0.3
0.2 0.6 0.7 0.5 0.5 0.6
0.6 0.6 0.4 0.5 0.6 0.3
2
0.2
0.7
0.7
0.8
0.7
0.8
0.8
0.6
0.6
0.7
0.2
0.3
R
0.2
0.7
0.2
0.3
0.9
0.3
0.9
0.7
0.2
0.3
0.7
0.8
x y

47. Inicializar los pesos de las neuronas
0.2 0.4 0.9 0.5 0.7 0.6
0.3 0.8 0.3 0.7 0.3 0.1
0.6 0.2 0.9 0.6 0.5 0.2
0.7 0.7 0.4 0.7 0.3 0.3
0.4 0.9 0.1 0.8 0.5 0.3
0.7 0.2 0.3 0.3 0.8 0.3
0.2 0.6 0.7 0.5 0.5 0.6
0.6 0.6 0.4 0.5 0.6 0.3
0.2 0.7 0.7 0.8 0.6 0.2
2
0.7 0.8 0.8 0.6 0.7 0.3
R
0.2
0.7
0.2
0.3
0.9
0.3
0.9
0.7
0.2
0.3
0.7
0.8
x y
Mapas autoorganizados/ Algoritmo de aprendizaje

48. Inicializar los pesos de las neuronas
0.2 0.4 0.9 0.5 0.7 0.6
1 0.3 0.8 0.3 0.7 0.3 0.1
0.6 0.2 0.9 0.6 0.5 0.2
0.7 0.7 0.4 0.7 0.3 0.3
0.4 0.9 0.1 0.8 0.5 0.3
0.7 0.2 0.3 0.3 0.8 0.3
w2 0.2 0.6 0.7 0.5 0.5 0.6
0.6 0.6 0.4 0.5 0.6 0.3
0.2 0.7 0.7 0.8 0.6 0.2
2
0.7 0.8 0.8 0.6 0.7 0.3
R
0 w1 1
0.2
0.7
0.2
0.3
0.9
0.3
0.9
0.7
0.2
0.3
0.7
0.8
x y

49. 5. Presentar una entrada a la red
0.14 0.77
0.2 0.4 0.9 0.5 0.7 0.6
1 0.3 0.8 0.3 0.7 0.3 0.1
0.6 0.2 0.9 0.6 0.5 0.2
0.7 0.7 0.4 0.7 0.3 0.3
0.4 0.9 0.1 0.8 0.5 0.3
0.7 0.2 0.3 0.3 0.8 0.3
w2 0.2 0.6 0.7 0.5 0.5 0.6
0.6 0.6 0.4 0.5 0.6 0.3
0.2 0.7 0.7 0.8 0.6 0.2
2
0.7 0.8 0.8 0.6 0.7 0.3
R
0 w1 1
0.2
0.7
0.2
0.3
0.9
0.3
0.9
0.7
0.2
0.3
0.7
0.8
x y
Mapas autoorganizados/ Algoritmo de aprendizaje

50. Presentar una entrada a la red
0.14 0.77
0.2 0.4 0.9 0.5 0.7 0.6
1 0.3 0.8 0.3 0.7 0.3 0.1
0.6 0.2 0.9 0.6 0.5 0.2
0.7 0.7 0.4 0.7 0.3 0.3
0.4 0.9 0.1 0.8 0.5 0.3
0.7 0.2 0.3 0.3 0.8 0.3
w2 0.2 0.6 0.7 0.5 0.5 0.6
0.6 0.6 0.4 0.5 0.6 0.3
0.2 0.7 0.7 0.8 0.6 0.2
2
0.7 0.8 0.8 0.6 0.7 0.3
R
0 w1 1
0.2
0.7
0.2
0.3
0.9
0.3
0.9
0.7
0.2
0.3
0.7
0.8
x y
Mapas autoorganizados/ Algoritmo de aprendizaje

51. 6. Encontrar la neurona ganadora
0.14 0.77
0.2 0.4 0.9 0.5 0.7 0.6
0.3 0.8 0.3 0.7 0.3 0.1
0.6 0.2 0.9 0.6 0.5 0.2
0.7 0.7 0.4 0.7 0.3 0.3
0.4 0.9 0.1 0.8 0.5 0.3
0.7 0.2 0.3 0.3 0.8 0.3
0.2 0.6 0.7 0.5 0.5 0.6
0.6 0.6 0.4 0.5 0.6 0.3
2
0.2
0.7
0.7
0.8
0.7
0.8
0.8
0.6
0.6
0.7
0.2
0.3
R
0.2 0.2 0.9 0.9 0.2 0.7
x y
0.7 0.3 0.3 0.7 0.3 0.8
Mapas autoorganizados/ Algoritmo de aprendizaje

52. Ajustar los pesos de la neurona ganadora
Ajustar los pesos de la neurona ganadora en la dirección del punto presente
en la entrada.
∆W = α(t) (X – W) , también los pesos de las neuronas de la vecindad de la
neurona ganadora.
Pero con una tasa de aprendizaje reducida (Sombrero Mejicano) de manera
que se especialice menos que la neurona ganadora.
Mapas autoorganizados/ Algoritmo de aprendizaje

53. 7. Presentar otro ejemplo
0.09 0.71
0.2 0.4 0.9 0.5 0.7 0.6
0.3 0.8 0.3 0.7 0.3 0.1
0.6 0.2 0.9 0.6 0.5 0.2
0.7 0.7 0.4 0.7 0.3 0.3
0.4 0.9 0.1 0.8 0.5 0.3
0.7 0.2 0.3 0.3 0.8 0.3
0.2 0.6 0.7 0.5 0.5 0.6
0.6 0.6 0.4 0.5 0.6 0.3
0.2 0.7 0.7 0.8 0.6 0.2
2
0.7 0.8 0.8 0.6 0.7 0.3
R
0.2
0.7
0.2
0.3
0.9
0.3
0.9
0.7
0.2
0.3
0.7
0.8
x y
Mapas autoorganizados/ Algoritmo de aprendizaje

54. Presentar otro ejemplo
0.09 0.71
0.2 0.4 0.9 0.5 0.7 0.6
0.3 0.8 0.3 0.7 0.3 0.1
0.6 0.2 0.9 0.6 0.5 0.2
0.7 0.7 0.4 0.7 0.3 0.3
0.4 0.9 0.1 0.8 0.5 0.3
0.7 0.2 0.3 0.3 0.8 0.3
0.2 0.6 0.7 0.5 0.5 0.6
0.6 0.6 0.4 0.5 0.6 0.3
0.2 0.7 0.7 0.8 0.6 0.2
2
0.7 0.8 0.8 0.6 0.7 0.3
R
0.2
0.7
0.2
0.3
0.9
0.3
0.9
0.7
0.2
0.3
0.7
0.8
x y
Mapas autoorganizados/ Algoritmo de aprendizaje

55. BMU (Best match unit)
Mapas autoorganizados/ Algoritmo de aprendizaje

56. Repetir
Reducir la vecindad de las neuronas y repetir 2 a 4 veces para todos los
puntos por un cierto numero de iteraciones
Mapas autoorganizados/ Algoritmo de aprendizaje

57. Visualización y funcionamiento del mapa
0.2 0.4 0.9 0.5 0.7 0.6
0.3 0.8 0.3 0.7 0.3 0.1
0.6 0.2 0.9 0.6 0.5 0.2
0.7 0.7 0.4 0.7 0.3 0.3
0.4 0.9 0.1 0.8 0.5 0.3
0.7 0.2 0.3 0.3 0.8 0.3
0.2 0.6 0.7 0.5 0.5 0.6
0.6 0.6 0.4 0.5 0.6 0.3
0.2 0.7 0.7 0.8 0.6 0.2
2
0.7 0.8 0.8 0.6 0.7 0.3
R
0.2
0.7
0.2
0.3
0.9
0.3
0.9
0.7
0.2
0.3
0.7
0.8
x y
Mapas autoorganizados/ Algoritmo de aprendizaje

58. Ejemplo
función de vecindad

59. Visualización y funcionamiento del mapa
•Una vez seleccionado el mapa óptimo, podemos pasar a la
fase de visualización observando en qué coordenadas del
mapa se encuentra la neurona asociada a cada patrón de
entrenamiento.
•Esto nos permite proyectar el espacio multidimensional de
entrada en un mapa bidimensional.
•Además de analizar la similitud entre los clusters o
agrupaciones de datos organizados por la propia red.
•Por este motivo, el modelo de mapa autoorganizado es
especialmente útil para establecer relaciones, desconocidas
previamente, entre conjuntos de datos.

60. Bondades de los mapas autoorganizados
Clustering: Actuar como clasificadores, encontrando patrones en los datos
de entrada y clasificándolos en grupos según estos patrones.
Reducción de dimensión: Representar datos multidimensionales en
espacios de mucha menor dimensión, normalmente una o dos
dimensiones, preservando la topología de la entrada.
Esto es muy útil cuando se trabaja con espacios multidimensionales (más
de tres dimensiones) que el ser humano no es capaz de representar, como
por ejemplo en problemas agro-ecológicos en los que intervienen
numerosas variables como temperatura, precipitación, humedad relativa,
etc.
Pre-tratamiento de datos: SOM trabaja con ausencia de datos
Análisis y comprensión de datos: SOM permite una presentación visual
sobre las relaciones entre variables

61. Visualización y funcionamiento del mapa
2
R
x y
Mapas autoorganizados/ Algoritmo de aprendizaje

62. Aplicacion