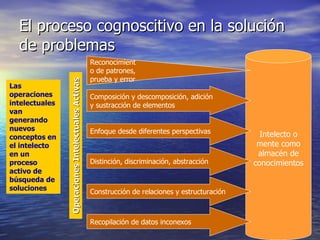
El documento describe los atributos de los problemas y el proceso de resolución de problemas. Explica que los problemas varían en su grado de estructuración, complejidad, dinamicidad y abstracción. También describe el proceso cognitivo de resolución de problemas, que implica construir un modelo mental del problema y manipularlo activamente para encontrar una solución. Finalmente, clasifica diferentes tipos de problemas como de lógica, algoritmos, toma de decisiones, diagnóstico, diseño y dilemas.

1. Resolución de Problemas Leonel Morales Díaz Ingeniería Simple [email_address] Disponible en: http://www.ingenieriasimple.com/problemas Copyright 2008 by Leonel Morales Díaz – Ingeniería Simple. Derechos reservados

2. Los Problemas “ Problema” tiene muchos significados Algunos no son agradables Insolubilidad, resignación, situación indeseable, necesidad insatisfecha Entrenamiento implica enseñar a resolver problemas Un conjunto particular

3. Dos atributos Primero: un problema es una entidad desconocida en un contexto particular La diferencia entre el estado actual y el estado objetivo Segundo: resolver el problema tiene que tener un valor Alguien debe creer que la solución aportará valor social, cultural, o intelectual Si nadie percive el valor de la solución, no hay percepción del problema

4. Problemas y soluciones Estado actual Estado intermedio Estado intermedio Estado intermedio Estado intermedio Estado intermedio Estado intermedio Estado deseado Lo desconocido

5. Atributos variables Los problemas varían en Conocimiento necesario para resolverlo Contexto en el que se presentan Proceso necesario para resolverlo Intelectualmente Grado de estructuración Complejidad Dinamicidad Abstracción o especificidad de dominio

6. Grado de estructuración Estructurados e Inestructurados Estructurados Planteamiento completo, con los datos necesarios Se usan mucho en la educación formal Inestructurados Ausencia de datos Informalidad del planteamiento Son los de la vida real

7. Bien estructurados Requieren un número limitado de Conceptos, reglas y principios Su dominio es restringido Bien definido Estado inicial Objetivo o meta de solución Procedimiento de solución conocido Contienen todos los elementos

8. Grado de estructuración Inestructurados También conocidos como perversamente estructurados Son los más comunes en la vida diaria y profesional No se ajustan a un dominio de estudio Son multidisciplinarios Su solución No se puede predecir No es convergente Contienen aspectos desconocidos

9. Solución a inestructurados Requieren conocimientos y técnicas de diversas ciencias Múltiples soluciones O múltiples métodos de solución O ninguna solución Se aplica el criterio antes que la técnica Múltiples criterios a veces Puede que no se conozca el criterio Se acude a la opinión

10. Grado de complejidad Se determina por Número de cuestiones o planteamientos a resolver Número de funciones Número de variables Y el grado de conexiones entre esas variables El tipo de relaciones funcionales entre estos aspectos Y su estabilidad en el tiempo

11. Grado de complejidad También influye Número, claridad y confiabilidad de los componentes representados en el problema La dificultad de un problema es proporcional a su complejidad Los grados de complejidad y estructuración se traslapan

12. Traslape entre complejidad y estructuración Usualmente Mayor complejidad implica menor estructuración Pueden existir Problemas inestructurados y simples Elegir qué ropa ponerse Problemas bien estructurados y complejos Jugar un video juego

13. Dinamicidad Problemas dinámicos El entorno, las tareas, y sus factores cambian en el tiempo Requieren adaptabilidad de quien resuelve Cambiar tácticas y técnicas Ejemplo: Inversiones en la bolsa Problemas estáticos No cambian factores en el tiempo

14. Abstracción o especificidad De dominio También conocido como contexto Los problemas en un contexto se resuelven diferente en otro Hay especialistas por contexto Ingenieros, matemáticos, polítcos, médicos, etc. La cultura organizacional también influye En una empresa resuelven de forma diferente que en otra O en diferentes municipios, familias, etc.

15. Atributos de los problemas Problemas sencillos Al variar uno de los 4 atributos principales de los problemas cambia el grado de dificultad del problema mismo Inestructuración Complejidad Dinamicidad Abstracción Es decir, los problemas pueden cambiar su grado de dificultad en 4 direcciones. Complejidad Inestructuración Abstracción Dinamicidad Complejidad Inestructuración Dinamicidad Complejidad Abstracción Dinamicidad Inestructuración Abstracción

16. Resolución de Problemas Problema: Algo desconocido que vale la pena conocer Resolver: Cualquier secuencia de operaciones cognitivas que buscan el mismo objetivo La solución: Es primero conocida Luego aplicada

17. El proceso cognitivo Construcción de un modelo mental del problema Entender el problema También conocido como el espacio del problema Manipulación activa del modelo Pensar, enfocar desde diferentes perspectivas, componer y descomponer, adición y sustracción, prueba y error (en la mente) Conocimiento y actividad son recíprocos Son procesos interdependientes

18. El proceso cognoscitivo en la solución de problemas Intelecto o mente como almacén de conocimientos Recopilación de datos inconexos Construcción de relaciones y estructuración Distinción, discriminación, abstracción Enfoque desde diferentes perspectivas Composición y descomposición, adición y sustracción de elementos Reconocimiento de patrones, prueba y error Las operaciones intelectuales van generando nuevos conceptos en el intelecto en un proceso activo de búsqueda de soluciones Operaciones Intelectuales Activas

19. Tipología de problemas Problema de lógica Algorítmico Problema-historia Problema de uso de regla Toma de decisiones Apagafuegos (saca-clavos) Diagnóstico y solución Estrategia y desempeño Análisis de caso Diseño Dilemas

20. Problema de lógica Aplicación lógica Manipulación de un número limitado de variables Ejemplos: Resolver un rompecabezas Demostrar un teorema De particular interés para Ciencias de la Computación Base de la matemática discreta, el cálculo de predicados y el álgebra booleana

21. Algorítmico Aplicación de procedimientos Secuencias de manipulaciones Aplicación de algoritmos a conjuntos similares de datos Producción de la respuesta correcta a partir de cálculos establecidos Ejemplos: Aplicación de fórmulas Cálculos matemáticos Derivadas, integrales, factorización, mínimo común múltiplo

22. Algorítmicos Computacionales Tipos comunes por la estrategia de solución Recursivos simples Avance y retroceso o backtracking Dividir y conquistar Programación dinámica Glotonería o greedy Ramificación y fronteras Fuerza bruta Ruta aleatoria Ascenso de colina Tipos comunes por la aplicación De ordenamiento De búsqueda De inserción de elemento De eliminación de elemento De procesamiento de cadenas de caracteres Algoritmos geométricos Grafos Matemáticos

23. Problema-historia Implica desambiguación Distinción de variables Seleccionar y aplicar un algoritmo Ejemplo: Problemas de física: “un automóvil se desplaza…” Construcción de esquema entidad-relación Automatización de facturación

24. Problema de uso de regla Aplicación de procedimientos Con restricciones o reglas Dadas las reglas: Seleccionar el procedimiento adecuado Encontrar la mejor respuesta con esas reglas Ejemplos: Problemas de optimización de producción Con restricciones de insumos, capital, horario, etc.

25. Toma de decisiones Usualmente requiere Identificar los diferentes cursos de acción Beneficios y limitaciones de cada curso Definición de criterios de ponderación Justificar la opción seleccionada Ejemplos: ¿Qué automóvil comprar? Selección de estrategia empresarial

26. Apagafuegos (saca-clavos) Examinar sistemas Ejecutar procedimientos de prueba Evaluar resultados Plantear y confirmar hipótesis sobre fallas Estrategias comunes: Reemplazo simple Eliminación en serie División espacial Ejemplos: Interrupciones en sistemas con uno o más fallos

27. Diagnóstico y solución En general es encontrar y resolver fallas Seleccionar diferentes opciones de tratamiento Con monitoreo constante Se necesita identificar bien el problema antes de aplicar la solución Ejemplos: Problemas de auditoría Obtención de resultados incongruentes en sistemas complejos

28. Estrategia y desempeño Situaciones que requieren aplicar tácticas para conseguir objetivos estratégicos, con restricciones de tiempo Optimizar el desempeño al mismo tiempo que se monitorea el entorno Presencia de competidores que dificultan el desempeño Ejemplos: Seguimiento de la estrategia empresarial Simulaciones de mercados, negocios, etc.

29. Análisis de caso Implican Identificación de la solución Alternativas de acción Respaldo de opiniones con argumentos Ejemplos: Coyunturas empresariales, políticas o sociales, con buen respaldo documental y tiempo disponible para resolver

30. Diseño Consiste en Identificar los objetivos Producir un artefacto Estructurar y articular el problema La solución es un artefacto A menudo los objetivos son vagos, las restricciones poco conocidas, y se requiere etapa de análisis No hay soluciones buenas o malas Solo mejores o peores Ejemplos: Proyectos de sistemas informáticos Otros proyectos de ingeniería Montaje de plantas de producción Construcción de edificios

31. Diseño e Ingeniería El diseño se considera la actividad intelectual de ingeniería por excelencia La ingeniería es Analizar científicamente una situación La ciencia de entender la situación actual Diseñar la situación deseada Construir la situación deseada de acuerdo al diseño

32. Dilemas Reconciliar cursos de acción Cada uno con Diferente grado de complejidad Resultados inciertos o impredecibles Decisiones molestas y difíciles de tomar Usualmente perspectivas irreconciliables Ejemplos: Estudiar o trabajar Cerrar una planta o relanzar el producto

33. Resumen La resolución de problemas es una habilidad básica de todo ser humano La necesidad de resolver problemas ha estado presente en toda la historia de la humanidad Desde la época de las cavernas, hasta la era espacial En el ingeniero esta habilidad está especialmente desarrollada No solo en el ámbito de su especialidad También porque está acostumbrado a enfrentar todo tipo de problemas en los proyectos que desarrolla La educación formal usualmente utiliza los problemas para desarrollar el intelecto Bien estructurados, poco dinámicos, algo complejos y específicos de un dominio Este no es el tipo de problemas con que nos encontramos día a día

34. Resumen Los problemas pueden incrementar su dificultad en 4 direcciones Grado de estructuración o inestructuración Complejidad Dinamicidad (variación en el tiempo) Abstracción La resolución de problemas es esencialmente un proceso cognitivo: La solución primero se conoce y después se aplica El proceso tiene dos partes: Construcción del modelo cognoscitivo del problema Manipulación activa del modelo