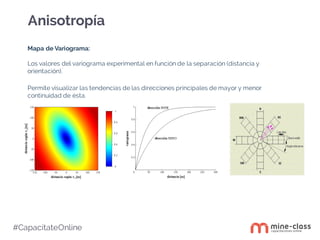
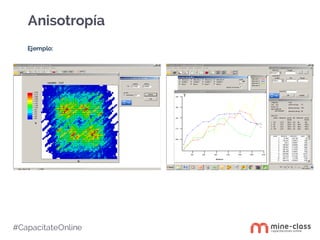
Este documento presenta información sobre el profesor Roberto Díaz y el curso de análisis variográfico que impartirá. El curso cubrirá temas como modelamiento y análisis de datos, variografía experimental, variografía estructural, variografía de indicadores y análisis de anisotropías. El objetivo es entregar los conocimientos básicos para analizar la correlación espacial de variables mediante la variografía experimental y variografía estructural.