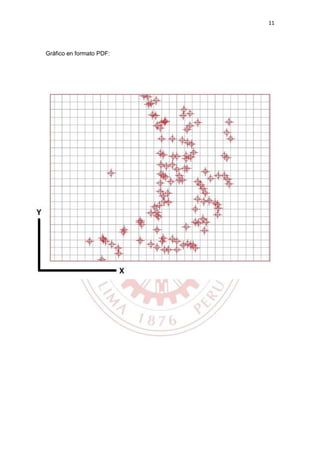
Este documento presenta el cálculo de variogramas promedios en diversas direcciones para estimar los recursos y reservas de un yacimiento. Inicialmente, se ubican 115 puntos espacialmente y se define el problema. Luego, se explican conceptos teóricos como variograma, variograma promedio y cálculo para mallas irregulares. Finalmente, se muestra el código para calcular los variogramas promedios en las direcciones N-S, E-W, NW-SE y NE-SW y graficarlos. El objetivo es estimar la distribuc

1. “AÑO DE LA LUCHA CONTRA LA CORRUPCIÓN Y LA IMPUNIDAD”
Facultad de Ingeniería Geológica, Minera y Metalúrgica
UNIVERSIDAD NACIONAL DE INGENIERÍA
Tema:
VARIOGRAMA PROMEDIO EN DIVERSAS DIRECIONES
Presentado por:
- Lincoln Rommel Angeles Guillen
- Lincoln Eduardo Esteban Pérez
- Meza Basilio Ronaldo
Curso:
GEOESTADÍSTICA
Docente:
Ph.D. VALERIANO ALFREDO MARIN SUAREZ
Ing. AUGUSTO TEVES ROJAS
23 de septiembre del 2019

2. 2
TABLA DE CONTENIDO
I. INTRODUCCION.................................................................................................................3
II. OBJETIVOS ........................................................................................................................4
III. MARCO TEORICO...........................................................................................................4
3.1. VARIOGRAMA............................................................................................................4
3.2. VARIOGRAMA PROMEDIO .........................................................................................5
3.3. CÁLCULO DEL VARIOGRAMA PARA MALLAS IRREGULARES.........................................6
IV. DEFINICION DEL PROBLEMA ..........................................................................................8
4.1. GRAFICA EN AUTOCAD ............................................................................................10
4.2. CODIGO PARA CALCULO DE VARIOGRAMA PROMEDIO EN DIVERSAS DIRECIONES...12
4.3. HISTOGRAMA..........................................................................................................14
4.4. DIRECCIÓN E-W .......................................................................................................15
4.5. DIRECCIÓN NE-SW...................................................................................................16
4.6. DIRECCIÓN N-S ........................................................................................................16
4.7. DIRECCIÓN SE-NW...................................................................................................17
V. CONCLUSIONES...............................................................................................................18
VI. BIBLIOGRAFÍA..............................................................................................................19

3. 3
I. INTRODUCCION
En el campo de las ciencias de la tierra es muy común encontrar variables
distribuidas espacialmente, para el estudio de estas variables son usados
diversos procedimientos geoestadísticos.
La geoestadística surge en la década del 50 a partir de estudios realizados con
el objetivo de obtener una mayor precisión en la estimación de recursos y
reservas minerales. Su punto de partida es el análisis de los fenómenos
distribuidos en el espacio (por ejemplo, la mineralización)
Hoy por hoy, los dominios de aplicación de la geoestadistica son amplios ya que,
a partir del estudio de la variabilidad de sus variables, se obtienen elementos
para predecir sus características. Además de la minería que es el campo que le
dio origen se pueden mencionar otras áreas de estudio tales como: el petróleo,
pesca, la salud, ingeniería civil, finanzas, cartografía, el medio ambiente, entre
otros. En el surgimiento y desarrollo hay tres elementos importantes que
destacar: la consolidación de la geoestadistica con los trabajos de G. Matheron
en 1965, el establecimiento de la escuela de Fontainebleau y finalmente el
desarrollo de la Geoestadística asociada con la informática.
En este informe se encontrará el inicio de la geoestadistica y aplicación de la
misma en el cálculo de estimación de recursos y reservas. En la primera parte
se dará el marco teórico necesario para el claro entendimiento de lo planteado
en el informe. Posteriormente se dará a conocer el planteamiento y desarrollo
del mismo, empleado para el cálculo del variograma promedio.

4. 4
II. OBJETIVOS
 Ubicar los puntos espacialmente con ayuda de Autocad.
 Calcular los variogramas para las direcciones N-S, E-W, NW-SE, NE-
SW, para el elemento CaCO3.
 Calcular el variograma promedio en las direcciones dadas.
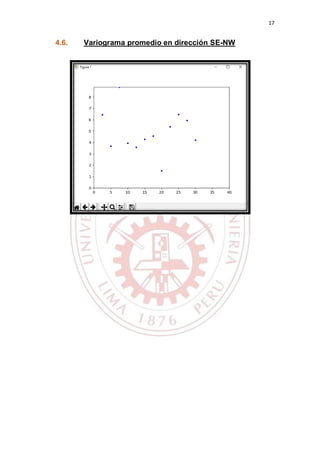
 Graficar los variogramas.
III. MARCO TEORICO
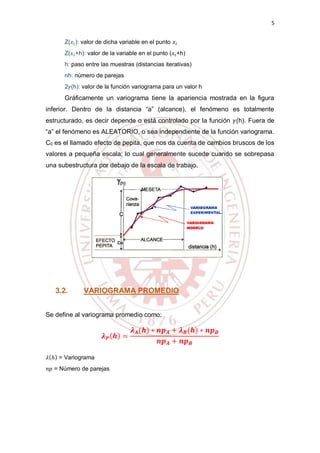
3.1. VARIOGRAMA
Es una función vectorial que permite medir las discrepancias de una propiedad
en una región del espacio. Siendo una herramienta de uso en el análisis de
reservas minerales en una región definida.
Una vez que se ha obtenido el variograma experimental y se ha estudiado su
comportamiento, el paso siguiente es encontrar algún modelo paramétrico que
ajuste adecuadamente los datos muestrales, esto es realizado por medio de
variogramas teóricos.
Los variogramas son realizados en varias direcciones para definir
adecuadamente el comportamiento de la propiedad estudiada en toda la
extensión del yacimiento, en caso de que se esté estudiando en un plano
horizontal. Dependiendo de los resultados se utilizará un método geoestadístico
u otro.
Los variogramas se calculan mediante la fórmula general
𝟐𝜸( 𝒉) =
∑ [ 𝒁(𝒙𝒊) − 𝒁(𝒙𝒊 + 𝒉)] 𝟐𝒏𝒉
𝒊=𝟏
𝒏𝒉
Donde:
Z: variable estudiada

5. 5
Z(𝑥𝑖): valor de dicha variable en el punto 𝑥𝑖
Z(𝑥𝑖+h): valor de la variable en el punto (𝑥𝑖+h)
h: paso entre las muestras (distancias iterativas)
nh: número de parejas
2𝛾(h): valor de la función variograma para un valor h
Gráficamente un variograma tiene la apariencia mostrada en la figura
inferior. Dentro de la distancia “a” (alcance), el fenómeno es totalmente
estructurado, es decir depende o está controlado por la función 𝛾(h). Fuera de
“a” el fenómeno es ALEATORIO, o sea independiente de la función variograma.
C0 es el llamado efecto de pepita, que nos da cuenta de cambios bruscos de los
valores a pequeña escala; lo cual generalmente sucede cuando se sobrepasa
una subestructura por debajo de la escala de trabajo.
3.2. VARIOGRAMA PROMEDIO
Se define al variograma promedio como:
𝝀 𝑷( 𝒉) =
𝝀 𝑨(𝒉) ∗ 𝒏𝒑 𝑨 + 𝝀 𝑩(𝒉) ∗ 𝒏𝒑 𝑩
𝒏𝒑 𝑨 + 𝒏𝒑 𝑩
𝜆(ℎ) = Variograma
𝑛𝑝 = Número de parejas

6. 6
3.3. CÁLCULO DEL VARIOGRAMA PARA MALLAS
IRREGULARES
En el caso bidimensional, la situación es la siguiente:
Aproximación: Método de los sectores. Se basa en la aproximación siguiente: “Dos
puntos están aproximadamente a la distancia h si una vez fijado el primero, el segundo
cae en la zona de la figura”:

7. 7
Si el punto P2 cae en la zona amarilla, entonces se dice que P1 y P2 están
aproximadamente a la distancia h. θ se llama tolerancia angular, ε se llama tolerancia
en distancia. La elección de θ y ε depende de la distribución espacial de los datos y de
la práctica. En algunos casos la práctica recomienda utilizar θ = 22.5º y ε = 0.5b, en que
b es la distancia mínima, llamada paso, para el cálculo de γ(h). 70 El paso en una
dirección dada se puede determinar como la distancia entre datos aproximadamente
contiguos en esa dirección. El método de aproximación presenta problemas:
 Puede caer más de un punto en la zona. En este caso se consideran las
diferencias en el cálculo.
 sí |h| es grande, como el ángulo se abre, la aproximación tiende a ser
grosera:
Algunos paquetes computacionales definen otro tipo de zona para evitar este problema
(método del lápiz):

8. 8
En este caso hay que definir tres parámetros: θ, ε y d (d se llama a veces ancho de
banda). Hay que tener presente que es necesario conocer bien el variograma en una
vecindad de h=0 (los puntos más cercanos al origen), luego, en algunas situaciones no
se justifica este método del lápiz.
IV. DEFINICION DEL PROBLEMA
Se planteó encontrar los variogramas promedios en las direcciones N-S, E-W,
NW-SE, NE-SW, para el elemento CaCO3, de acuerdos a las siguientes
ubicaciones y leyes de mineral.
Leyes X Y Z Leyes X Y Z
0.871 507 318 20 0.974 436 128 20
0.864 513 307 20 0.904 502 153 20
0.863 524 279 20 0.909 563 223 20
0.899 518 293 20 0.908 557 208 20
0.897 528 276 20 0.902 526 160 20
0.893 516 308 20 0.939 504 150 20
0.901 522 292 20 0.974 465 124 20
0.919 528 243 20 0.88 577 283 20
0.876 512 317 20 0.962 473 119 20
0.913 529 228 20 0.957 524 143 20
0.871 530 262 20 0.956 502 129 20
0.887 532 241 20 0.973 452 104 20
0.906 529 216 20 0.964 474 112 20
0.917 528 193 20 0.95 516 124 20
0.899 530 283 20 0.918 577 183 20
0.875 534 284 20 0.882 587 219 20
0.889 523 312 20 0.931 577 206 20

9. 9
0.938 528 204 20 0.881 615 270 20
0.893 535 285 20 0.951 581 202 20
0.905 532 214 20 0.825 618 284 20
0.916 453 132 20 0.957 584 197 20
0.936 536 226 20 0.951 574 170 20
0.905 544 262 20 0.922 587 191 20
0.89 535 212 20 0.911 532 132 20
0.92 545 239 20 0.948 531 128 20
0.95 521 173 20 0.966 562 147 20
0.853 544 228 20 0.912 594 210 20
0.881 532 187 20 0.926 544 131 20
0.906 533 180 20 0.944 585 180 20
0.924 527 175 20 0.944 524 120 20
0.906 558 292 20 0.956 534 117 20
0.898 557 260 20 0.928 604 214 20
0.902 550 239 20 0.936 574 153 20
0.873 563 274 20 0.951 539 117 20
0.862 564 257 20 0.948 550 128 20
0.948 568 238 20 0.953 578 152 20
0.894 550 222 20 0.947 550 117 20
0.929 542 206 20 0.952 592 181 20
0.877 538 191 20 0.953 558 123 20
0.852 559 300 20 0.945 584 157 20
0.909 562 240 20 0.968 564 125 20
0.908 516 165 20 0.971 568 123 20
0.896 569 255 20 0.929 612 214 20
0.94 502 155 20 0.89 616 209 20
0.91 562 236 20 0.893 600 178 20
0.894 481 143 20 0.893 618 203 20
0.867 524 166 20 0.968 603 176 20
0.923 454 130 20 0.898 612 240 20
0.885 524 162 20 0.908 464 217 20
0.908 567 279 20 0.967 571 123 20
0.9 553 214 20 0.97 588 153 20
0.893 539 179 20 0.942 574 119 20
0.963 457 128 20 0.956 604 171 20
0.912 567 295 20 0.921 615 237 20
0.916 560 223 20 0.961 586 142 20
0.912 553 208 20 0.945 603 163 20
0.948 480 140 20 0.924 620 262 20
0.919 572 244 20

10. 10
4.1. GRAFICOS EN AUTOCAD
En los siguientes tres gráficos se representa los 115 puntos ubicados a una misma
cota igual a 20m.
Gráfico en Autocad en vista 2D:
Gráfico en Autocad en vista 3D

11. 11
Gráfico en formato PDF:

12. 12
CODIGO PARA CALCULO DE VARIOGRAMA PROMEDIO EN DIVERSAS
DIRECIONES

13. 13

14. 14
4.2. HISTOGRAMA
Estadísticos
Leyes (Agrupada)
N Válido 115
Perdidos 0
Leyes (Agrupada)
Frecuencia Porcentaje
Porcentaje
válido
Porcentaje
acumulado
Válido <= ,844 1 ,9 ,9 ,9
,845 - ,863 4 3,5 3,5 4,3
,864 - ,882 12 10,4 10,4 14,8
,883 - ,901 20 17,4 17,4 32,2
,902 - ,920 27 23,5 23,5 55,7
,921 - ,939 13 11,3 11,3 67,0
,940 - ,958 25 21,7 21,7 88,7
,959+ 13 11,3 11,3 100,0
Total 115 100,0 100,0

15. 15
4.3. Variograma promedio en dirección E-W
Media = 0.908
Desviación Estándar=1.713
N = 115

16. 16
4.4. Variograma promedio en dirección NE-SW
4.5. Variograma promedio en dirección N-S

17. 17
4.6. Variograma promedio en dirección SE-NW

18. 18
V. CONCLUSIONES
 Como se ha utilizado la misma cota (eje Z), se obtiene un plano
bidimensional.
 Se concluye que los variogramas promedio N-S y E-W, tienen un
comportamiento parecido.
 Se concluye que los variogramas promedio NW-SE y NE-SW, tienen
un comportamiento parecido.
 Se concluye que el variograma solo depende de la inter distancia entre
los datos.
 La programación es realmente útil, de otro modo hubiese sido difícil la
realización del presente trabajo.

19. 19
VI. BIBLIOGRAFÍA
Ph. D Marín Suárez. APUNTES EN CLASE, DOCUMENTOS QUE NOS
MUESTRA CON AYUDA DEL PROYECTOR
Samuel Canchaya M. “EL MÉTODO GEOESTADÍSTICO: UNA
PRESENTACIÓN COMPARATIVA CON LOS MÉTODOS
TRADICIONALES DE ESTIMACIÓN DE RESERVAS”.
http://geoestadistica.org/index.html, página del CENTRO
GEOESTADÍSTICO PERUANO, Lima 12 de mayo del 2013
Denilson Araujo Gutierrez (2018, julio 12). Uso del SGEMS – Parte 1.
Recuperado de: Escriba aquí la ecuación.
https://www.youtube.com/watch?v=dymJKjh7Uts&feature=youtu.be