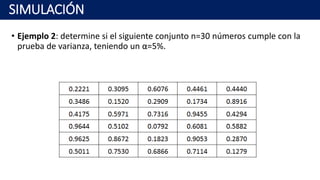
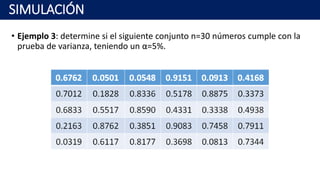
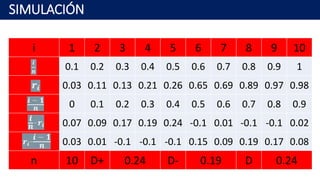
Este documento presenta los fundamentos de los números pseudoaleatorios y varios métodos para generarlos, como el método de cuadrados medios, el algoritmo de productos medios, y algoritmos congruenciales lineales, multiplicativos y aditivos. Explica que los números pseudoaleatorios deben distribuirse uniformemente, ser estadísticamente independientes y reproducibles sin repetición dentro de una longitud determinada.

1. TECNOLÓGICO NACIONAL DE MÉXICO
Ingeniería en Sistemas Computacionales
Simulación
Unidad II: Números Pseudoaleatorios
Material de clase desarrollado para la asignatura de Simulación para Ingeniería en Sistemas Computacionales
SIMULACIÓN

2. FUNDAMENTOS DE INGENIERÍA DE SOFTWARE
Competencias:
• Conocer la diferencia entre un número aleatorio y un pseudoaleatorio.
• Identificar y aplicar los métodos de generación de números pseudoaleatorios.
• Aplicar e interpretar las pruebas estadísticas a los números pseudoaleatorios.
• Seleccionar el generador de números pseudoaleatorios a utilizar en la unidad siguiente.
• Aplicar el método de Montecarlo a la solución de un problema matemático.

3. • Se llama números pseudoaleatorios a una sucesión determinística de
números en el intervalo [0,1] que tiene las mismas propiedades estadísticas
que una sucesión de números aleatorios. Los números pseudoaleatorios son
necesarios cuando se pone en práctica un modelo de simulación, para obtener
observaciones aleatorias a partir de distribuciones de probabilidad. Los
números aleatorios generados en un inicio por una computadora casi siempre
son números aleatorios enteros
GENERACIÓN DE NÚMEROS PSEUDOALEATORIOS
SIMULACIÓN

4. • La aplicación de los números aleatorios se remonta a los tiempos de la
primera revolución industrial, cuando los procesos manuales tuvieron
que reemplazarse por procesos mecanizados como consecuencia de la
explosión demográfica que se estaba presentando en los países
desarrollados con la disminución de las tasas de mortalidad y el aumento
de las tasas de natalidad y que, para satisfacer las necesidades de la
población cada vez más creciente hubo necesidad de incrementar la
producción de toda clase de bienes y servicios.
SIMULACIÓN

5. • El procedimiento usado por una computadora para generar números
aleatorios se llama: GENERADOR DE NÚMEROS ALEATORIOS
• La referencia a secuencias de números aleatorios significa que: el
algoritmo produce muchos números aleatorios en serie.
• Es posible identificar diferentes métodos usados a través de la historia
para generar números aleatorios que pudieran ser utilizados en los
procesos de simulación de las actividades industriales. Dichos métodos
pudiéramos clasificarlos en:
1. Manuales
2. Tablas de Biblioteca
3. Generadores Analógicos
4. Generadores Digitales
5. Métodos de Recurrencia o Congruenciales
SIMULACIÓN

6. Método de los cuadrados medios
• Procedimiento:
1. Seleccionar un valor para semilla número entero, positivo, con e
dígitos par
2. Elevar al cuadrado no, completar con ceros a la izquierda del número
hasta tener 2*e dígitos, seleccionar los e dígitos centrales del
número como ni
3. Calcular
4. Repetir 2 y 3 tantas veces como sea necesario.
SIMULACIÓN

7. Ejemplo:
• Suponga que se desean generar números aleatorios por el método de los
cuadrados medios con 1111 como semilla y e=8.
SIMULACIÓN

8. Ejercicio
• Generar 20 números pseudoaleatorios en base a la semilla 1572 con e=3
• Genere la tabla correspondiente
SIMULACIÓN

9. Algoritmo de los Productos Medios
• La mecánica de generación de números pseudoaleatorios de este
algoritmo no congruencial es similar a la del algoritmo de cuadrados
medios. La diferencia entre ambos radica en que el algoritmo de
productos medios requiere dos semillas, ambas con D dígitos; además,
en lugar de elevarlas al cuadrado, las semillas se multiplican y del
producto se seleccionan los D dígitos del centro, los cuales formarán el
primer número pseudoaleatorio r¡ = 0.D dígitos.
SIMULACIÓN

10. • Después se elimina una semilla, y la otra se multiplica por el primer
número de D dígitos, para luego seleccionar del producto los D dígitos
que conformarán un segundo número r(.. Entonces se elimina la segunda
semilla y se multiplican el primer número de D dígitos por el segundo
número de D dígitos; del producto se obtiene el tercer número r¡.
Siempre se irá eliminando el número más antiguo, y el procedimiento se
repetirá hasta generar los n números pseudo aleatorios.
SIMULACIÓN

11. A continuación se presentan con más detalle los pasos del método para
generar números con el algoritmo de producto medios.
• 1. Seleccionar una semilla (X0) con D dígitos (D > 3).
• 2. Seleccionar una semilla (X}) con D dígitos (D > 3).
• 3. Sea V0 = XQ*X:; sea X2 = los D dígitos del centro, y sea r. = 0.D dígitos del
centro.
• 4. Sea f¡ = X*XÍ+1; sea X¡+2 = los D dígitos del centro, y sea rí+1 = 0.D dígitos del centro para
toda f¡= 1,2,3,...,/?;
• 5. Repetir el paso 4 hasta obtener los n números r¡ deseados.
Nota: Si no es posible obtener los D dígitos del centro del número /^agregue
ceros a la izquierda del número Y¡.
SIMULACIÓN

12. Ejemplo
• Generar los primeros 5 números r¡ a partir de las semillas X0 = 5 015 y
X1, = 5 734; observe que ambas semillas tienen D = 4 dígitos.
SIMULACIÓN

13. Algoritmo de multiplicador constante
• Este algoritmo no congruencial es similar al algoritmo de productos medios.
Los siguientes son los pasos necesarios para generar números
pseudoaleatorios con el algoritmo de multiplicador constante .
1. Seleccionar una semilla (X0) con D dígitos (D > 3).
2. Seleccionar una constante (a) con D dígitos (D > 3).
3. Sea YQ - a*X0; sea X, = los D dígitos del centro, y sea r¡ = 0.D dígitos del
centro.
4. Sea Y¡ = a*X¡; sea X/+1 = los D dígitos del centro, y sea rM = 0.D dígitos del
centro para toda /' = 1,2,3,..., n.
5. Repetir el paso 4 hasta obtener los n números f. deseados.
Nota: Si no es posible obtener los D dígitos del centro del número Yjt agregue
ceros a la izquierda del número Yr
SIMULACIÓN

14. Ejemplo: Generar los primeros 5 números pseudoaleatorios r¡ a partir de
la semilla X0 = 9 803 y con la constante a = 6 965. Observe que tanto la
semilla como la constante tienen D = 4 dígitos, e=3.
SIMULACIÓN

15. Algoritmo lineal
• Este algoritmo congruencial fue propuesto por D. H. Lehmer, en 1951. Según
Law y Kel-ton, este algoritmo ha sido el más usado. El algoritmo congruencial
lineal genera una secuencia de números enteros por medio de la siguiente
ecuación recursiva:
Xí+1 = (aX(. + c)mod(m) /'=0,1,2,3,n
• Donde X0 es la semilla, a es la constante multiplicativa, c es una constante
aditiva y m es el módulo; X0 >0, a >0, c>0 y m>0 deben ser números enteros.
La operación "mod m" significa multiplicar X( por a, sumar c y dividir el
resultado entre m para obtener el residuo X/+1.
SIMULACIÓN

16. • Es importante señalar que la ecuación recursiva del algoritmo
congruencial lineal genera una secuencia de números enteros
S = {0,1,2,3, ...,m - 1},y que para obtener números pseudo aleatorios en
el intervalo (0,1) se requiere la siguiente ecuación:
SIMULACIÓN

17. Ejemplo: Generar 4 números entre O y 1 con los siguientes parámetros:
X0 = 37, a = 19, c = 33 y m = 100.
SIMULACIÓN

18. Algoritmo congruencial multiplicativo
• El algoritmo congruencial multiplicativo surge del algoritmo congruencial lineal
cuando c = 0. Entonces la ecuación recursiva es:
• En comparación con el algoritmo congruencial lineal, la ventaja del algoritmo
multiplicativo es que implica una operación menos a realizar. Los parámetros de
arranque de este algoritmo son XQI a y m, todos los cuales deben ser números
enteros y mayores que cero.
SIMULACIÓN

19. • Para transformar los números X(. en el intervalo (0,1) se usa la ecuación r¡
- x.J{m - 1). De acuerdo con Banks, Carson, Nelson y Nicollas condiciones
que deben cumplir los parámetros para que el algoritmo congruencial
multiplicativo alcance su máximo periodo son:
SIMULACIÓN

20. • Generar suficientes números entre 0 y 1 con los siguientes parámetros:
X0 = 17, k = 2 y g = 5, hasta encontrar el periodo o ciclo de vida.
Solución: a = 5+8(2) = 21; m=32
SIMULACIÓN

21. Algoritmo congruencial aditivo
• Este algoritmo requiere una secuencia previa de n números enteros
X1, X2, X3, X4,...,Xn para generar una nueva secuencia de números enteros que
empieza en Xn+1, Xn+2, Xn+3, Xn+4,... Su ecuación recursiva es:
SIMULACIÓN

22. Ejemplo: Generar 7 números pseudoaleatorios entre cero y uno a partir de la
siguiente secuencia de números enteros: 65, 89, 98, 03, 69; m = 100. X0 = 60.
Sean X1 = 65, X2 = 89, X3 = 98, X4 = 03, X5 = 69.
Para generar ev r2, ry,r4, r5, r6 y r7 antes es necesario generar X^, X^, X^, X^, X^,
X^, X^.
SIMULACIÓN

23. Algoritmos congruenciales no lineales
Algoritmo congruencial cuadrático
SIMULACIÓN

24. Ejemplo: Generar, a partir del algoritmo
congruencial cuadrático, suficientes
números enteros hasta alcanzar el
periodo de vida, considerando los
parámetros:
X0 = 13, m = 8, a = 26, b = 27 y c = 27.
Como todas las condiciones estipuladas
para los parámetros se satisfacen, es de
esperarse que el periodo de vida del
generador sea N = m = 8, tal como podrá
comprobar al revisar los cálculos
correspondientes, que se presentan a
continuación.
SIMULACIÓN

25. PRUEBAS DE ALEATORIEDAD
SIMULACIÓN

26. 1) Distribución Uniforme
2) Independencia (no correlacionados)
ADEMÁS SON IMPORTANTES LOS SIGUIENTES ASPECTOS:
a) Las subsecuenticas también deben cumplir 1) y 2)
b) Deben ser secuencias largas y sin huecos (densas)
c) Algoritmos rápidos y que no demanden mucha memoria.
HIPÓTESIS
SIMULACIÓN

27. • NÚMEROS ALEATORIOS ENTEROS. Es una observación aleatoria de una
distribución uniforme sincretizada en el intervalo n, n+1… Por lo general,
n =0 ó 1 donde estos son valores convenientes para la mayoría de las
aplicaciones
• NÚMEROS ALEATORIOS UNIFORMES. Es una observación aleatoria a partir de
una distribución uniforme (continua) en un intervalo [a, b]
LOS NÚMEROS ALEATORIOS SE PUEDEN DIVIDIR EN DOS CATEGORÍAS PRINCIPALES:
SIMULACIÓN

28. • Ajustarse a una distribución U (0,1).
• Ser estadísticamente
independientes (no debe deducirse
un número conociendo otros ya
generados).
• Ser reproducibles (la misma semilla
debe dar la misma sucesión).
• Ciclo repetitivo muy largo.
• Facilidad de obtención.
• Ocupar poca memoria.
PROPIEDADES MÍNIMAS QUE DEBERÁN SATISFACER LOS NÚMEROS
PSEUDOALEATORIOS:
SIMULACIÓN

29. DEBEN SER:
1. Uniformemente distribuidos
2. Estadísticamente independientes
3. Reproducibles
4. Sin repetición dentro de una longitud
determinada de la sucesión
5. Generación a grandes velocidades
6. Requerir el mínimo de capacidad de
almacenamiento Instituto
CONDICIONES
SIMULACIÓN

30. • Las propiedades estadísticas que deben poseer los números pseudoaleatorios
generados por los métodos congruenciales tienen que ver con independencia
y aleatoriedad estadísticas.
PRUEBAS ESTADÍSTICAS DE ALEATORIEDAD
SIMULACIÓN

31. • Una de las propiedades que deben cumplir los números del conjunto r¡, es
que el valor esperado sea igual a 0.5. La prueba que busca determinar lo
anterior es la llamada prueba de medias, en la cual se plantean las
siguientes hipótesis:
• La prueba de medias consiste en determinar el promedio de los n números
que contiene el conjunto r¡, mediante la ecuación siguiente:
SIMULACIÓN
Hipótesis Nula
Hipótesis Interna

32. Prueba de Medias
• Esta prueba consiste en verificar que los números generados tengan una
media estadísticamente igual a ½ o 0.5, de este modo la hipótesis planteada
es:
• Paso 1, Calcular la media de los n números generados
• Paso 2, Calcular los límites superior e inferior de aceptación.
• Paso 3, Si el valor se encuentra entre li y ls, aceptamos que los números
tienen una media estadísticamente igual a ½ con un nivel de aceptación
1-α.
SIMULACIÓN

33. • Ejemplo
SIMULACIÓN

34. Ejercicio
SIMULACIÓN

35. • Ejercicio
SIMULACIÓN

36. Prueba de Varianza
• Otra propiedad que debe satisfacer el conjunto de ri, es que sus números
tengan una varianza de 1/12. la prueba que busca determinar lo anterior es
la prueba de varianza, que establece las siguientes hipótesis:
• H0: σ2
ri=1/12
• H1: σ2
ri≠1/12
SIMULACIÓN

37. • La prueba de varianza consiste en determinar la varianza de los n números
que contiene ri, mediante la ecuación siguiente:
• Después se calculan los limites de aceptación inferior y superior con las
ecuaciones siguientes:
SIMULACIÓN

38. • Si el valor de V(r) se encuentra entre los límites de aceptación, decimos:
• No se puede rechazar que el conjunto ri tiene una varianza de 1/12, con
un nivel de aceptación de 1-α;
• De lo contrario, se rechaza que el conjunto ri tiene una varianza de 1/12.
SIMULACIÓN

39. • Ejemplo: realizar la prueba de varianza a los 40 números ri de la siguiente
tabla. Considerando que n=40 y α=5%, procedemos a calcular la varianza de
los números, y los límites de aceptación correspondientes
SIMULACIÓN

40. • Resultados
SIMULACIÓN
Chi
Cuadrada

41. • Dado que el valor de la varianza: V(r)=0.087034 está entre los limites de
aceptación, podemos decir que no se puede rechazar que el conjunto de 40
números ri tiene una varianza de 1/12= 0.08333.
SIMULACIÓN

42. • Ejemplo 2: determine si el siguiente conjunto n=30 números cumple con la
prueba de varianza, teniendo un α=5%.
SIMULACIÓN

43. • Ejemplo 3: determine si el siguiente conjunto n=30 números cumple con la
prueba de varianza, teniendo un α=5%.
SIMULACIÓN

44. • Una de las propiedades más importantes que debe cumplir un conjunto de
números ri es la uniformidad.
• Para comprobar su acatamiento se han desarrollado pruebas estadísticas
tales como las pruebas Chi-cuadrada y de Kolmogorov-Smirnov .
• En cualquiera de ambos cosas, para probar la uniformidad de los números
de un conjunto ri es necesario formular las siguientes hipótesis:
Prueba de Chi-Cuadrada
SIMULACIÓN

45. Tenemos dos hipótesis:
•Ho: ri~U(0,1) (es distribución uniforme)
•H1: ri no son uniformes
SIMULACIÓN

46. • La prueba Chi-cuadrada busca determinar si los números del
conjunto ri se distribuyen uniformemente en el intervalo (0,1).
• Para llevar a cabo esta prueba es necesario dividir el intervalo
(0,1), en m subintervalos, en donde es recomendable m=√n.
• Posteriormente se clasifica cada número pseudo aleatorio del
conjunto ri en los m intervalos .
SIMULACIÓN

47. • A la cantidad de números ri que se clasifican en cada
intervalo se le denomina frecuencia observada (Oi), y a la
cantidad de números ri que se espera encontrar en cada
intervalo se le llama frecuencia esperada (Ei); teóricamente,
la ri es igual a n/m. A partir de los valores de Oi y Ei se
determina el estadístico mediante la ecuación:
SIMULACIÓN

48. Si el valor del estadístico es menor al valor de tablas de , entonces
no se puede rechazar que el conjunto de números ri sigue una distribución
uniforme. En caso contrario, se rechaza que ri sigue una distribución
uniforme.
SIMULACIÓN

49. SIMULACIÓN
• Ej. Realizar la prueba de chi-cuadrada a los siguientes 100 números de un
conjunto ri, con un nivel de confianza del 95% y a=5%

50. Cálculos para la prueba chi-cuadrada
SIMULACIÓN

51. • El estadístico =6.2 es menor al estadístico correspondiente de la
chi- cuadrada =16.9. En consecuencia, no se puede rechazar
que los números ri siguen una distribución uniforme.
Resultado
𝑿 𝟎.𝟎𝟓,𝟗
𝟐
SIMULACIÓN

52. • Ejercicio: Realizar la prueba de chi-cuadrada a los siguientes 100 números de
un conjunto ri, con un nivel de confianza del 95% y a=5%
SIMULACIÓN

53. • Ejercicio: Realizar la prueba de chi-cuadrada a los siguientes 100 números de
un conjunto ri, con un nivel de confianza del 99% y a=1%
SIMULACIÓN
0.9550 0.8932 0.0828 0.3670 0.2364 0.4713 0.1902 0.9972 0.8630 0.6944
0.4048 0.1691 0.9587 0.4497 0.3330 0.8932 0.2024 0.2133 0.7432 0.5486
0.8930 0.8930 0.6384 0.2322 0.4678 0.5872 0.4035 0.3151 0.2168 0.4510
0.1505 0.4461 0.5730 0.6885 0.4465 0.7365 0.3029 0.6068 0.6507 0.4593
0.6742 0.7428 0.5764 0.9657 0.4596 0.7932 0.9662 0.1931 0.8500 0.6076
0.2990 0.6736 0.3407 0.7466 0.9325 0.0098 0.8561 0.2708 0.8821 0.2515
0.1750 0.7691 0.2763 0.0421 0.8792 0.2516 0.4566 0.8877 0.7192 0.7397
0.1938 0.9258 0.8053 0.7505 0.8296 0.4957 0.2403 0.0769 0.1835 0.7654
0.2169 0.2935 0.8560 0.6746 0.8516 0.6540 0.1670 0.9600 0.7875 0.5586
0.6455 0.3088 0.4140 0.9188 0.1937 0.9959 0.6978 0.2760 0.8005 0.8569

54. • Propuesta por Kolmogorov-Smirnov, esta es una prueba estadística que
también nos sirve para determinar si un conjunto ri cumple la propiedad de
uniformidad.
• Es recomendable aplicarla en conjuntos ri pequeños, por ejemplo n<20. El
procedimiento es el siguiente:
Prueba de Kolmogorov-Smirnov
SIMULACIÓN

55. 1. Ordenar de menor a mayor los números del conjunto ri.
r1≤r2 ≤r3 ≤… ≤rn
2. Determinar los valores de D+, D- y D con las siguientes ecuaciones:
SIMULACIÓN

56. 3. Determinar el valor critico de acuerdo con la tabla de valores críticos de
Kolmogorov-Smirnov para un grado de confianza α, y según el tamaño de la
muestra n.
4. Si el valor D es mayor que el valor critico: Se concluye que los números del
conjunto ri no siguen una distribución uniforme; de lo contrario se dice que
no se ha detectado diferencia significativa entre la distribución de los números
del conjunto ri y la distribución uniforme.
SIMULACIÓN

57. Ej. Realizar una prueba de Kolgomorov-Smirnov, con un nivel de
confianza de 90%, al siguiente conjunto ri de 10 números
Para determinar los valores de D+, D- y D es recomendable
realizar una tabla como la siguiente:
SIMULACIÓN
ri = 0.97 0.11 0.65 0.26 0.98 0.03 0.13 0.89 0.21 0.69

58. SIMULACIÓN
i 1 2 3 4 5 6 7 8 9 10
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0.03 0.11 0.13 0.21 0.26 0.65 0.69 0.89 0.97 0.98
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
0.07 0.09 0.17 0.19 0.24 -0.1 0.01 -0.1 -0.1 0.02
0.03 0.01 -0.1 -0.1 -0.1 0.15 0.09 0.19 0.17 0.08
n 10 D+ 0.24 D- 0.19 D 0.24

59. • De acuerdo con la tabla de valores para la prueba de Kolmogorov-
Smirnov, el valor crítico; correspondiente a n=10
es =0.368, que resulta mayor al valor D=.24;
por lo tanto, se concluye que los números del conjunto ri, se
distribuyen uniformemente.
SIMULACIÓN

60. Ejercicio: Realizar una prueba de Kolgomorov-Smirnov, con un nivel de
confianza de 95%, al siguiente conjunto ri de 10 números
Para determinar los valores de D+, D- y D realice la tabla
correspondiente:
SIMULACIÓN
ri = 0.7012 0.1828 0.8336 0.5178 0.8875 0.6833 0.5517 0.8590 0.4331 0.3338

61. SIMULACIÓN