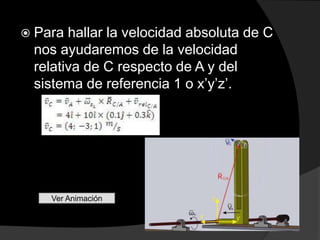
El documento presenta un problema de cinemática que involucra el movimiento de una esferita B en un disco giratorio. Se pide calcular la velocidad de B, la aceleración angular del disco, y las aceleraciones de B en los ejes x, y y z. Para resolverlo, se ubican dos sistemas de referencia móviles y se aplica el método de movimiento relativo para hallar primero las velocidades y aceleraciones absolutas del punto A, luego del punto C, y finalmente de la esferita B.

1. TEACHER : Ing. Tito Roberto Vílchez Vílchez
Comité de Solución y Revisión
GRUPO Anampa Vargas, Anthony Vicente 20091101D
•Colán Quevedo, Gustavo Arturo 20091012A
7 •Sánchez Villalobos, Kenny Alexis 20091100H

2. *(C)* En el mecanismo mostrado la esferita B entra con
una velocidad y aceleración de 5 m/s y 2 m/s² relativa
al disco, a su vez el extremo A se mueve linealmente
con vA=4 I m/s y aA=3 I m/s². La barra doblada AC
tiene ω1=10 I rad/s, α1= 4 I rad/s², a su vez el disco
gira respecto de AC con ω2=25 J rad/s, α2= 3 J
rad/s², para el instante mostrado calcule:
10. La magnitud de la velocidad lineal de la esferita B. (m/s)
11. La magnitud de la aceleración angular del disco. (rad/s²)
12.La magnitud absoluta de la aceleración de B en el eje X. (m/s²)
13.La magnitud absoluta de la aceleración de B en el eje Y. (m/s²)
14. La magnitud absoluta de la aceleración de B en el eje Z. (m/s²)

4. Para resolver este problema lo primero que haremos
es ubicar dos sistemas móviles, uno en A que girará
junto con AC y otro en C que girará con el disco.
Teniendo nuestros sistemas móviles adecuadamente
ubicados procederemos a hacer los cálculos
respectivos.

5.  Teniendo ya los datos necesarios, procederemos a reemplazar
en nuestras ecuaciones

6. Para hallar la magnitud de la velocidad lineal de la esferita B
hallaremos primero la velocidad y luego hallaremos su módulo.
Para hallar la velocidad de B usaremos el método de
movimiento relativo, que nos permitirá hallar la velocidad
absoluta de A, luego la de C y, finalmente, la de B.
La velocidad absoluta de A es dato del problema
Ver Animación

7.  Para hallar la velocidad absoluta de C
nos ayudaremos de la velocidad
relativa de C respecto de A y del
sistema de referencia 1 o x’y’z’.
Ver Animación

8.  Análogamente, para la velocidad de B nos ayudaremos de la
velocidad relativa de B respecto de C y del sistema 2 o
x’’y’’z’’
Ver Animación 1
Ver Animación 2
Ver Animación 3

9. Y tenemos la velocidad, ahora solo
tenemos que calcular el módulo

10.  Para hallar la aceleración angular absoluta del disco
tendremos en cuenta que nuestro sistema 2 o x’’y’’z’’ es un
sistema móvil, ubicado en la unión de C y el disco, que gira
con el disco, y claro está, con la misma velocidad y
aceleración angular. Entonces bastará con hallar la
aceleración angular del sistema 2 o x’’y’’z’’.

11.  Paradar nuestra respuesta debemos
calcular su módulo

12.  Para hallar la aceleración absoluta de B usaremos el
mismo método, el de movimiento relativo, hallando
primero la aceleración absoluta de A, luego la de C y,
finalmente, la de B.
 Una vez que tengamos la aceleración absoluta de B
extraeremos la componente en cada eje para dar
nuestras respuestas
 Hallar la aceleración de A no será mayor problema
pues es dato
Ver Animación

13.  Para hallar la aceleración de C nos ayudaremos
de la aceleración de A y del sistema 1 o x’y’z’.
Ver Animación

14.  Análogamente para hallar la aceleración de B usaremos la
aceleración de C, ya conocida, y el sistema 2 o x’’y’’z’’
Ver Animación 1
Ver Animación 2
Ver Animación 3

15.  Una vez que tengamos la aceleración absoluta de B
extraeremos la componente en cada eje para dar nuestras
respuestas, así tendremos:

16.  “Exígete mucho a ti mismo y espera poco
de los demás. Así te ahorrarás disgustos.”
(Confucio)
 “No hay que confundir nunca el
conocimiento con la sabiduría. El primero
nos sirve para ganarnos la vida; la sabiduría
nos ayuda a vivir.” (Sorcha Carey)

17. Gracias por su atención