Este documento presenta una prueba objetiva y de ensayo sobre conceptos de cálculo diferencial e integral. La prueba objetiva contiene 30 afirmaciones sobre derivadas, funciones, máximos y mínimos, concavidad, entre otros temas. La prueba de ensayo presenta 10 preguntas abiertas sobre estos mismos conceptos para que el estudiante los explique y aplique al resolver problemas matemáticos.

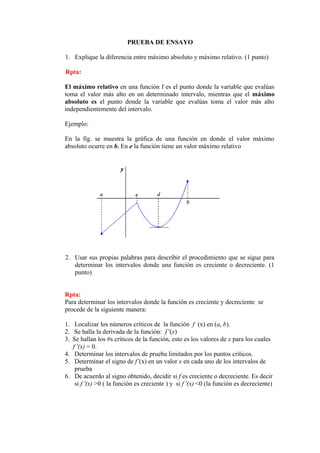
1. MATEMÁTICA I
SEGUNDA EVALUACIÓN A DISTANCIA
PRUEBA OBJETIVA
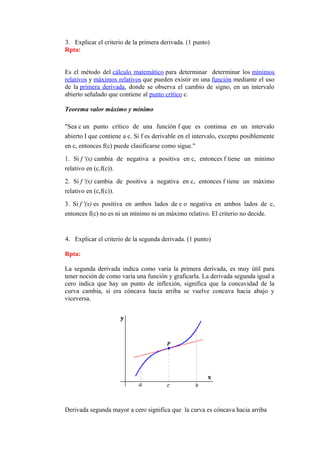
Encierre en un círculo la letra V si es verdadero o F si es falso, en cada una de las
siguientes afirmaciones. (Cada respuesta correcta vale 0,2 de punto)
dy
1. V F Si y = e −x (cos x + sen x) , entonces = − e −x sen x .
2
dx
dy
2. V F Si y = x(ln x −1) , entonces = x ln x .
dx
d f ´(x)
3. V F Si f es derivable, entonces f ( x) = .
dx 2 x
d 2
4. V F x + x = 2 x +1 .
dx
dy 1
5. V F = , si sen y = x + y 5 .
dx cos y − 5 y 4
6. V F El valor máximo de la función f ( x) = cos x + sen x, en el intervalo
π π
[− , ] es 2.
2 2
7. V F La función f(x) = x3 – 27x es decreciente en el intervalo (-3, 3).
8. V F f ( x ) = 5 x 2 / 3 − 2 x 5 / 3 tiene un mínimo relativo en x = 0 y un
máximo
relativo en x = 1.
x 2 +1
9. V F f ( x) = es creciente en el intervalo (-∞, -1) y tiene un
1 − x2
extremo
relativo en x = -1.
10. V F Si f es continua en el intervalo [a, b], f tiene máximo y mínimo absoluto.
11. V F El valor máximo absoluto de f(x) = x4ln x en (0, e] es e4 y el valor
1
mínimo absoluto es − .
4e
12. V F La gráfica de f ( x ) = x 4 −8 x 3 es cóncava hacia abajo en (4, +∞).
1 1
13. V F ( , 2 ) es un punto de inflexión de la gráfica de f ( x) = x ln 2 x .
e e
14. V F Si f(x) = sen2 (2x), entonces f´(x) = 2(sen2x)(cos2x).
15. V F Si y es una función derivable de u, u es una función derivable de v, y v es
dy dy du dv
una función derivable de x, entonces =
dx du dv dx
16. V F La función y = 2 sen x + 3 cos x satisface la ecuación y´´ + y = 0.
17. V F Para la función y = 2x2 + sen 2x, se tiene que y´´ = 4 – 4 sen 2x.
18. V F El máximo absoluto de una función que es continua en un intervalo
cerrado puede ocurrir en desvalores diferentes en el intervalo.
19. V F Si f es una función continua en un intervalo cerrado, entonces tiene un
mínimo absoluto en el intervalo.
20. V F Si x = c es un punto crítico de la función f, entonces también es un
número crítico de la función g(x) = f (x – k),donde k es una constante.

2. 1
21. V F El teorema del valor medio puede aplicarse a f ( x) = en el intervalo
x
[-1, 1].
22. V F Si f´(x) = 0 para todo x en el dominio de f, entonces f es una función
constante.
23. V F Si la gráfica de una función polinómica tiene tres intersecciones con el
ejes, entonces debe tener al menos dos puntos en los cuales su recta
tangente es horizontal.
24. V F La suma de dos funciones crecientes es creciente.
25. V F Existe un máximo o un mínimo relativo en cada punto crítico.
26. V F Todo polinomio de grado n tiene (n – 1) puntos críticos.
27. V F Si f´´ (2) = 0, entonces la gráfica de f debe tener un punto de inflexión en
x = 2.
28. V F La gráfica de todo polinomio cúbico tiene precisamente un punto de
inflexión.
29. V F Sean f y g son funciones derivables, con f´´ ≠ 0 y g´´ ≠ 0. si f y g son
cóncavas hacia arriba en el intervalo (a, b), entonces f + g es también
cóncava hacia arriba en (a, b).
30. V F Si (c, f(c )) es un punto de inflexión de la gráfica de f, entonces
f´´ (c ) = 0 o f´´ no existe en c.

3. PRUEBA DE ENSAYO
1. Explique la diferencia entre máximo absoluto y máximo relativo. (1 punto)
Rpta:
El máximo relativo en una función f es el punto donde la variable que evalúas
toma el valor más alto en un determinado intervalo, mientras que el máximo
absoluto es el punto donde la variable que evalúas toma el valor más alto
independientemente del intervalo.
Ejemplo:
En la fig. se muestra la gráfica de una función en donde el valor máximo
absoluto ocurre en b. En e la función tiene un valor máximo relativo
2. Usar sus propias palabras para describir el procedimiento que se sigue para
determinar los intervalos donde una función es creciente o decreciente. (1
punto)
Rpta:
Para determinar los intervalos donde la función es creciente y decreciente se
procede de la siguiente manera:
1. Localizar los números críticos de la función f (x) en (a, b).
2. Se halla la derivada de la función: f '(x)
3. Se hallan los #s críticos de la función, esto es los valores de x para los cuales
f '(x) = 0.
4. Determinar los intervalos de prueba limitados por los puntos críticos.
5. Determinar el signo de f’(x) en un valor x en cada uno de los intervalos de
prueba
6. De acuerdo al signo obtenido, decidir si f es creciente o decreciente. Es decir
si f '(x) >0 ( la función es creciente ) y si f '(x) <0 (la función es decreciente)

4. 3. Explicar el criterio de la primera derivada. (1 punto)
Rpta:
Es el método del cálculo matemático para determinar determinar los mínimos
relativos y máximos relativos que pueden existir en una función mediante el uso
de la primera derivada, donde se observa el cambio de signo, en un intervalo
abierto señalado que contiene al punto crítico c.
Teorema valor máximo y mínimo
"Sea c un punto crítico de una función f que es continua en un intervalo
abierto I que contiene a c. Si f es derivable en el intervalo, excepto posiblemente
en c, entonces f(c) puede clasificarse como sigue."
1. Si f '(x) cambia de negativa a positiva en c, entonces f tiene un mínimo
relativo en (c,f(c)).
2. Si f '(x) cambia de positiva a negativa en c, entonces f tiene un máximo
relativo en (c,f(c)).
3. Si f '(x) es positiva en ambos lados de c o negativa en ambos lados de c,
entonces f(c) no es ni un mínimo ni un máximo relativo. El criterio no decide.
4. Explicar el criterio de la segunda derivada. (1 punto)
Rpta:
La segunda derivada indica como varia la primera derivada, es muy útil para
tener noción de como varia una función y graficarla. La derivada segunda igual a
cero indica que hay un punto de inflexión, significa que la concavidad de la
curva cambia, si era cóncava hacia arriba se vuelve concava hacia abajo y
viceversa.
Derivada segunda mayor a cero significa que la curva es cóncava hacia arriba

5. , y si es menor a cero significa que es cóncava hacia abajo.
5. Una fábrica de chocolates le ha hecho un pedido a la empresa Envases
metálicos S.A. El pedido requiere cajas metálicas abiertas para envasar
chocolates. Los diseñadores de Envases metálicos especifican que cada caja
debe hacerse a partir de una hoja cuadrada de metal de 60 centímetros de
lado; en ele proceso de manufactura se pide que se corten cuadrados
idénticos en cada esquina y luego se doblan las salientes resultantes.
Explique como usar funciones para matematizar este problema y determine
las dimensiones de la caja más grande que puede fabricarse con estas
condiciones. (2,5 puntos).

6. 6. Las aristas de un cubo se expanden a un ritmo de 5 centímetros por segundo.
¿A qué ritmo cambia el área de su superficie cuando sus aristas tienen 4,5
centímetros?.
(1,5 puntos)
7. Determina los extremos absolutos de la función f(x) = x 3 – 12x en el
intervalo [-1, 1].
(1,5 puntos)
8. Determina los intervalos de concavidad de la gráfica de f ( x ) = x 4 −8 x 3 .
(1,5 puntos)
x +1
2
9. Obtenga los intervalos donde la función f ( x) = es creciente o
1 − x2
decreciente y los extremos relativos (si existen) de la misma.
(1,5 puntos)
10. Determina (si existen) los extremos relativos de f ( x) = 5 x − 2 x 5 / 3 .
2/3
(1,5 puntos)