Aplicaciones de la derivada: recta tangente, máximos, mínimos y puntos de inflexión

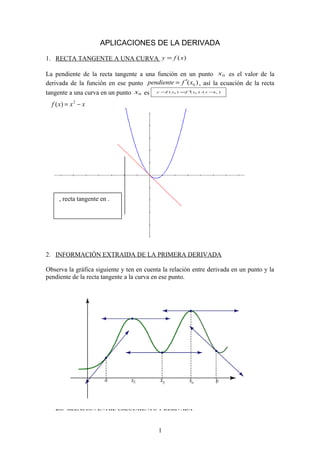
APLICACIONES DE LA DERIVADA

1. RECTA TANGENTE A UNA CURVA y = f (x)

La pendiente de la recta tangente a una función en un punto x0 es el valor de la
derivada de la función en ese punto pendiente = f ′( x0 ) , así la ecuación de la recta
tangente a una curva en un punto x0 es y −f ( x ) =f ′ x ) ⋅( x − )
0 ( 0 x
o

f ( x) = x 2 − x

, recta tangente en .

2. INFORMACIÓN EXTRAIDA DE LA PRIMERA DERIVADA

Observa la gráfica siguiente y ten en cuenta la relación entre derivada en un punto y la
pendiente de la recta tangente a la curva en ese punto.

2.1. RELACIÓN ENTRE CRECIMIENTO Y DERIVADA

1

f (x ) derivable y creciente en x0 ⇒ f ′( x0 ) ≥ 0
f (x ) derivable y decreciente en x0 ⇒ f ′( x0 ) ≤ 0

Ejemplo:

y = x 3 es derivable en todo R y su derivada es y ′ = 3x 2 . La gráfica es

se observa que en
x0 = 0 la función es
creciente (de hecho, es
creciente en todo su
dominio), luego la
derivada en ese punto
tendrá que ser mayor o
igual a 0. Efectivamente
f ′(0) = 0 ≥ 0 (
f ′( x) ≥ 0 para todo x)

2.2. CRITERIO PARA IDENTIFICAR INTERVALOS CRECIENTES O DECRECIENTES

f ′( x) > 0 ⇒ f es creciente
f ′( x) < 0 ⇒ f es decreciente

2.3. MÁXIMOS Y MÍNIMOS RELATIVOS

2.3.1. CONDICIÓN NECESARIA DE MÁXIMO O MÍNIMO RELATIVO

Si f (x ) es derivable en x0 , entonces
f (x ) tiene un máximo o un mínimo en x0 ⇒ f ′( x0 ) = 0

Sin embargo no es una condición suficiente, porque puede ocurrir que la derivada en un punto
valga 0 y que no haya máximo ni mínimo , como en x0 = 0 en el ejemplo y = x 3 .

2.3.2. REGLA PARA SABER SI UN PUNTO SINGULAR ES MÁXIMO O
MÍNIMO RELATIVO

2

Para saber si un punto singular (puntos que anulan la derivada) es máximo o mínimo
relativo de una función estudiaremos el signo de la derivada primera de la función.

Ejemplo:

y = x 3 − 27 x

Si calculamos su derivada y estudiamos el signo se tiene,
y ′ = 3 x 2 − 27 = 3 ⋅ ( x 2 − 9 ) = 3 ⋅ ( x + 3) ⋅ ( x − 3)

Luego podríamos decir que la función
• crece en ( −∞,−3) ∪( 3, ∞)
• decrece en ( −3,3)

Así que hay un máximo relativo en ( −3, f ( −3) ) y un mínimo relativo en ( 3, f (3) )
−∞ -3 3 3
-3 ∞
3 + + +
( x + 3) - + +
( x −3) - - +
Signo
y′ + - +
como se observaba en la gráfica.

3. INFORMACIÓN EXTRAIDA DE LA SEGUNDA DERIVADA

Una función es cóncava en un intervalo si la rectas tangentes a la función en ese
intervalo están por debajo de la función. Una función es convexa en un intervalo si la
rectas tangentes a la función de ese intervalo están por encima.

3

La denominación de convexidad y concavidad depende del punto de vista que se adopte
para considerar que es una concavidad, esto es si se mira a la función "desde arriba" o
"desde abajo". Por ello, es frecuente que en ocasiones se adopten las denominaciones
cóncava hacia arriba y cóncava hacia abajo para evitar las ambigüedades.

Los puntos donde la función cambia de curvatura se llaman puntos de inflexión.

3.1. RELACIÓN DE LA CURVATURA CON LA SEGUNDA DERIVADA

Si observamos la gráfica siguiente veremos que cuando la función es cóncava las
pendientes de las rectas
tangentes (las derivadas)
tienen un valor cada vez
más grande, y cuando es
convexa cada vez menor.

Criterios de concavidad o
convexidad:

• Por la derivada
primera:

a. Si una
función es
cóncava las
pendientes de las tangentes aumentan (f´ es creciente).
b. Si una función es convexa las pendientes de las tangentes disminuyen (f´
es decreciente).

• Por la derivada segunda:

Si f es cóncava hacia arriba  entonces f´ creciente, por lo tanto f´´ ≥ 0

Si f es cóncava hacia abajo  entonces f´ decreciente, por lo tanto f´´ ≤ 0

Si f ( x ) es derivable en x0 y tiene un punto de inflexión en x0 ⇒ f ′′( x0 ) = 0

3.2. CRITERIO PARA IDENTIFICAR INTERVALOS CÓNCAVOS Y CONVEXOS

Si una función es derivable dos veces, se tiene

f ′′( x ) > 0 ⇒ f es cóncava
f ′′( x ) < 0 ⇒ f es convexa

4

Ejemplo:

EJERCICIOS DE APLICACIONES DE LAS DERIVADAS

5

 2x − 3 si x <4
1º) Comprueba que la función f ( x ) =  cumple las
− x + 10x − 19 x ≥4
2
si
hipótesis del Teorema de Rolle en el intervalo [0, 8]. Averigua dónde cumple la
tesis.

x 2 + ax si x <3
2º) Calcula a, b y c para que la función f ( x ) =  cumpla las
 bx + c si x ≥3
hipótesis del Teorema de Rolle en el intervalo [0, 8]. Di en qué punto cumple la
tesis.

π
3º) Halla el valor de k para que la función f ( x ) = kx + tgx cumpla el Teorema de
2 3
Rolle en el intervalo [π/6,π/3].
 1 / x si − 2 ≤ x ≤ −1
 2
4º) Comprueba que la función f ( x ) =  x − 3 satisface las
 2 si − 1 ≤ x ≤ 0

hipótesis del Teorema del Valor Medio del Cálculo Diferencial. Calcula el valor o
valores donde se cumple la tesis.

5º) Comprueba que la función f(x) = |x – 2| no cumple las condiciones del Teorema del
Valor Medio del Cálculo Diferencial en el intervalo [0, 3].

6º) Estudia si el Teorema de Lagrange (o del Valor Medio del Cálculo Diferencial) se
 x3 x <0
puede aplicar a la función: f ( x) =  en el intervalo [–1, 2].
e − 1 x ≥ 0
x

7º) Sea f(x) una función continua y derivable en IR tal que f(0) = 3. Calcula cuánto tiene
que valer f(5) para asegurar que en (0, 5) existe un valor c tal que f ’(c) = 8.

8º) Determinar, si es posible, a y b para que el Teorema del Valor Medio del Cálculo
Diferencial sea aplicable a la función:
 a
 x si − 2 ≤ x ≤ −1
f (x) =  2
 x − b si − 1 < x ≤ 0
 2

9º) ¿Se puede aplicar el Teorema de Rolle a la función f(x) = |sen x| en el intervalo [π/3,
4π/3]? Razona la respuesta.

10º) Enuncia el teorema que asegura la existencia de solución del siguiente problema y
resuélvelo:
Halla el punto de tangencia de una recta paralela a la cuerda de la curva y = e x
definida por los puntos (0, 1) y (1, e).

11º) Determina un punto de la función f(x) = x3 en el que la recta tangente sea paralela a
la recta que pasa por los puntos (0, 0) y (2, 8).

6

x3
12º) Sea la función f ( x) = . ¿Puede cumplir la tesis del Teorema del Valor Medio
x +1
del Cálculo Diferencial en el intervalo [-2, 5]?. Justifícalo.

13º) Sea f(x) una función continua en el intervalo cerrado [a, b], con derivada segunda
en el intervalo (a, b). Demuestra que si f(x) = 0 en al menos tres valores de x ∈ [a,
b], entonces f ‘’(x) = 0 para algún x ∈ [a, b].

14º) Razona si son aplicables los Teoremas de Rolle y del Valor Medio del Cálculo
Diferencial a la función f(x) = tg x en [0, π].

15º) Si una función f(x) verifica las hipótesis del Teorema de Rolle, ¿verifica también
las del Teorema del Valor Medio del Cálculo Diferencial? ¿Que diferencia hay en
las conclusiones de ambos teoremas en ese caso?

16º) Dada la función f ( x ) = x 3 + ax 2 + bx + c :
a) Halla a, b y c para que la función admita un extremo relativo en x = 2 y un
punto de inflexión en x = 0, siendo f (−1) = −5 .
b) Para los valores anteriores de a, b y c, hallar:
b1) Los extremos relativos de la función.
b2) Los valores máximo y mínimo de dicha función en el intervalo [-3, 5].

1− x
17º) Determina la ecuación de la recta tangente a la gráfica de f ( x) = , en su
ex
punto de inflexión. Estudia la concavidad y convexidad de f(x).

18º) a) Define el concepto de máximo relativo de una función f(x) en un punto x = a y
enunciar su relación con las derivadas sucesivas de f(x) en x = a .
b) Determinar si la función f ( x) = x 2 − sen 2 x tiene un máximo relativo en x = 0 .

19º) Dada la función f ( x) = ( x −1)( x − 2)( x − 3)( x − 4) , halla tres intervalos tales
que cada uno contenga una raíz diferente de la ecuación f ´(x) = 0 .

20º) Si el término independiente de un polinomio en x es igual a 3 y el valor que toma
ese polinomio para x = 2 es 3, prueba que su derivada se anula para algún valor de x;
razona que ese valor pertenece a un cierto intervalo que se especificará.

21º) Demuestra que la ecuación x 3 + 6 x 2 + 15 x − 23 = 0 no puede tener más de una raíz
real. (Sugerencia: averigua si la primera derivada del polinomio se anula en algún
punto).

22º) Demuestra que la ecuación x18 − 5 x + 3 = 0 no puede tener más de dos raíces reales.
(Sugerencia: localiza los puntos en que se anula la derivada del primer miembro y ver
cuántos son, para deducir lo dicho).

7

23º) Comprueba, utilizando los teoremas de Bolzano y Rolle, que la curva
y = x 5 − 5 x −1 tiene exactamente tres puntos de intersección con el eje OX.

24º) Calcula los siguientes límites:

x 3 − 3x − 2 x2 + x +1
1) lim 2) lim 3)
x →2 x2 − 4 x →∞ x2 − x

x − sen x
lim
x →0 cos x −1
(1 − cos x ) sen x tg x − x
4) lim 5) lim 6)
x →0 x 2 x →0 x − sen x

e x − e sen x
lim
x →0 x3

7) lim
e x − e −x − 2x
8) lim
(
x ex −1 ) 9)
x →0 x − sen x x →0 cos x − senx + x − 1

x cos x − sen x
lim
x →0 x3
1 − cos( x −1)
10) lim 11) xlim+ x ⋅ ln x 12)
x→ 1 ( ln x ) 2 →0

lim ( x − 1) ln ( x − 1)
x →1+

13) lim( tg x ⋅ ln x ) , x>0
x →0
14) xlim 2 cos x ⋅ ln ( tg x )
→π /
15)

1 + x 
lim x ⋅ ln 
x →∞
 x 

 1  e 1 
16) lim c tg x −  17) lim x −  18)
x →0
 x x →1 e − e
 x −1 

 x 1 
lim − 

x →1 ln x x ⋅ ln x 

8

1 − cos x
19) lim(1 − cos x ) c tg x 20) lim 21)
x →0 x→ 0
(e x
−1 ) 2

x ⋅ arcsen x
lim
x →0 sen x ⋅ cos x

22) lim( c tg x ) 23) x lim 4( tg x )
sen x 1 / cos 2 x sen x
x →0 →π /
24) lim x
x →0
,

x>0

25) x lim 2( tg x ) 26) lim( e + x )
cos x x 3 1/ x

→π / x →0
27)

lim(1 + sen x )
cos ec ( x / 2 )
x →0

28) lim( cos x + 3 sen x )
2/ x 1/ x
x →0
29) lim x
x →∞
30)

lim x x a − 1
x →∞

25º) Estudia y representa gráficamente las siguientes funciones:
x 2 +1 x
1) y = 2) y = 3)
x x −1
2

x
y=
x − 5x + 4
2

4x x2 x
4) y = 5) y = 6) y = 1 + x
x +4
2
x +1
x 2 −1 ln x
7) y = 8) y = e1 / x 9) y =
x x

ex x 2 ln x si x >0
10) y = 11) y = 12) y = e x − e −x
x  0 si x =0

13) y = x ln x
2
14) y = x 2 e −x 15)
y = ( x −1)e −x

9

26º) En un libro los márgenes superior e inferior deben ser de 3 cm. y los márgenes
laterales de 2 cm. Si cada página tiene una superficie de texto impreso de 96 cm 2,
¿cuáles son las dimensiones si se sabe que el gasto de papel ha sido mínimo?

27º) Se quiere construir un marco para una ventana de 1 m 2 de área. El coste del marco
se estima en 6 € por cada metro de alto y 3 € por cada metro de ancho. ¿Cuáles son
las dimensiones del marco más económico?

28º) Se desea construir una caja abierta, de base cuadrada y 864 dm 3 de capacidad.
¿Cuáles han de ser sus dimensiones para que su superficie sea mínima?

29º) Con una plancha de cartón cuadrada de 12 dm de lado, se quiere construir una caja
con el mayor volumen posible, cortando cuadrados iguales en las esquinas y
doblando luego la plancha de forma adecuada. ¿Qué lado debe tener el cuadrado
que se ha de cortar?

30º) Calcula las dimensiones que debe tener un bote cilíndrico de hojalata cuyo
volumen es 8π m3, si queremos que la hojalata empleada en su fabricación sea
mínima. Considera los casos siguientes:
a) El bote sólo tiene tapa inferior.
b) El bote tiene dos tapas.

31º) De todos los triángulos rectángulos cuyos catetos suman 10 cm, halla las
dimensiones del que tenga área máxima.

32º) En un jardín con forma de semicírculo de radio 10 m se quiere construir un parterre
rectangular; uno de los lados del rectángulo está sobre el diámetro y el lado opuesto
tiene sus extremos en la curva. Calcula las dimensiones del parterre para que su área sea
máxima.

33º) Se quiere construir un depósito cilíndrico de área total 54 cm2. Determina el radio
de la base y la altura del cilindro para que el volumen sea máximo.

34º) De todas las rectas que pasan por el punto P(1, 2), encuentra la que determina con
los ejes de coordenadas (en el primer cuadrante) un triángulo de área mínima.

10

EJERCICIOS DE SELECTIVIDAD

Septiembre de 1996
1.- A. Enunciado de la Regla de L’Hôpital.
x − sen( x )
B. Calcular lim
x →0 sen( x 2 )

Junio de 1997
2.- A. Enunciado de la Regla de L’Hôpital.
( x −1) e x +1
B. Calcular el límite siguiente: lim
x →0 sen 2 ( x )

Septiembre de 1997
3.- A. ¿Existen funciones polinómicas de tercer grado que no tengan ningún punto de
inflexión? Razonar la respuesta.
B. Calcular los intervalos de concavidad, convexidad y los puntos de inflexión de la
función f(x) = sen(x) + cos(x) definida en el intervalo [0, 2π].

Junio de 1998
4.- A. ¿Puede ocurrir que exista el x→x0 f ( x ) y que la función f(x) no sea continua en
lim
x0? Razonar la respuesta.
B. Calcular el límite lim( e − x )
x 1/ x

x →0

Septiembre de 1998
5.- De todos los rectángulos de área la unidad, halla las dimensiones de aquel que tiene
mínimo el producto de las dos diagonales.

Junio de 1999
6.- La curva y = x 3 + a· x 2 + b· x + c corta al eje OX en x = 1 y tiene un punto de
inflexión en el punto (3, 2). Calcular los puntos de la curva que tengan recta tangente
paralela al eje OX.

Septiembre de 1999
7.- En un triángulo isósceles de base 12 cm (el lado desigual) y altura 10 cm, se inscribe
un rectángulo de manera que uno de los lados esté sobre la base del triángulo y los otros
dos vértices sobre los lados iguales. ¿Qué dimensiones debe tener el rectángulo de área
máxima?

Septiembre de 2000
8.- A. ¿Puede tener una función polinómica de grado dos un punto de inflexión? Razona
la respuesta.

11

B. Estudia la concavidad, convexidad y puntos de inflexión de la función:
ln ( x )
f ( x) =
x
Junio de 2002
x 2 − 2x + 2
9.- Dada f ( x ) = , escriba la ecuación de la secante a f que une los puntos
x −4
(-2, f(-2)) y (2, f(2)). ¿Existe un punto c en el intervalo [-2, 2] verificando que la
tangente a la gráfica de f en (c, f(c)) es paralela a la secante que ha hallado? En caso
afirmativo razone su respuesta y calcule c, en caso negativo razone porqué no existe.

Septiembre de 2002
10.- Calcule la ecuación de la recta que pasa por el punto (3, 1) y tal que el área del
triángulo formado por esta recta y los semiejes positivos coordenados sea mínima.

Septiembre de 2003
11.- A) Dada la parábola f ( x) = ax 2 + bx + c , determine los valores de a, b y c sabiendo
1
que f tiene un máximo en el punto de abscisa x = − y la recta tangente a f en el
2
punto (1,3) es y = -3x+ 6.
B) Determine el área de la región limitada por la gráfica de la función
1
f ( x) = x 2 + x + 5 , el eje OX y las rectas x = − e y = x + 6.
2

Junio de 2004
12.- A) Un barco B y dos ciudades A y C de la costa forman un triángulo rectángulo en
C. Las distancias del barco a las ciudades A y C son 13 Km y 5 Km respectivamente.
Un hombre situado en A desea llegar hasta el barco B. Sabiendo que puede nadar a 3
Km/h y caminar a 5 Km/h, ¿a qué distancia de A debe abandonar la costa para nadar
hasta B si quiere llegar lo antes posible?
4
B) Demuestre que la función f dada por f ( x) = es estrictamente
x + x−2 2

positiva en [2,+ ) y halle el área de la región determinada por la gráfica de f , el
∞
eje de abscisas y las rectas x=2 y x=3.

Junio 2005
13.- A. Enunciado de la Regla de L´Hôpital.
B. Calcule la relación entre a y b para que sea continua en toda la recta real la
función f : R → R definida por:
 e ax − 1
 , si x ≠ 0
f (x ) =  2x
 b, si x = 0


12

Junio 2006
14.- Opción 1. a) Calcula la ecuación de la recta tangente a la gráfica de f(x) = (x + 1)
e −x en el punto de corte de f(x) con el eje OX.
b) Calcula, para f(x) = (x + 1) e −x : intervalos de crecimiento y decrecimiento,
extremos relativos, puntos de inflexión, concavidad y convexidad.
c) Enunciado e interpretación geométrica del Tª del Valor Medio del Cálculo
Integral.

Junio 2006
15.- Opción 2. a) Enunciado e interpretación geométrica del Tª del Valor Medio del
Cálculo Diferencial.
b) De entre todos los triángulos rectángulos de hipotenusa 10 cm, calcula las
longitudes de los catetos que corresponden al de área máxima.
c) Área de un recinto.

Septiembre 2006
b
16.- Opción 1. a) Calcula los valores de a y b para que la gráfica de f(x) = a x +
x
tenga un mínimo relativo en el punto (½, 4). Para esos valores de a y b, calcula:
asíntotas e intervalos de crecimiento y decrecimiento de f(x).
x 2 ex
b) Calcula lim
x →0 cos 2 x − 1
c) Teoría de Cálculo Integral.

Septiembre 2006
17.- Opción 2. a) Definición de función continua en un punto. ¿Qué tipo de
x2
discontinuidad tiene en x=0 la función f(x) = ?
x
b) Un alambre de 170 cm de longitud se divide en dos partes. Con una de las
partes se quiere formar un cuadrado y con la otra un rectángulo de modo que la
base mida el doble que la altura. Calcula las longitudes de las partes en las que se
tiene que dividir el alambre para que la suma de las áreas del cuadrado y del
rectángulo sea mínima.
c) Área de un recinto.

Junio 2007
18.- Opción 1. b) Dada g ( x) = ax 4 + bx + c , calcula los valores a,b,c para que g(x) tenga
en el punto (1,-1) un mínimo relativo y la recta tangente a la gráfica de g(x), en x=0, sea
paralela a la recta y=4x.

13

Opción 2. a) Enunciado e interpretación geométrica del teorema de Rolle.
b) Dada f ( x) = x 3 − 9 x , calcula para f(x): puntos de corte con los ejes,
intervalos de crecimiento y decrecimiento, máximos y mínimos relativos, intervalos de
concavidad y convexidad y puntos de inflexión.

Septiembre 2007
e x senx − x
19.- a)Calcula lim .
x →0 2 x 2 + x 4

b) Calcula los vértices y el área del rectángulo de área máxima que se puede construir
de modo que su base esté sobre el eje OX y los vértices del lado opuesto estén sobre la
parábola y = −x 2 +12 .

Junio 2008
mx 2 − 1 + cos x
20.- Calcula el valor de m para que: lim =0.
x →0 sen( x 2 )

Razón de cambio y razones relacionadas

LA DERIVADA COMO RAZON DE CAMBIO

Puede interpretarse el concepto de la velocidad en el movimiento rectilíneo, estudiada
en la sección 4.2, como el concepto más general de la razón de cambio instantáneo. Es
esta una razón de cambio de la distancia respecto al tiempo, y si s = f (t ) describe un
movimiento rectilíneo, está razón de cambio en cualquier instante t, está representada
por f ′ ( t0 ) . De modo semejante a menudo nos interesamos en una razón de cambio de
una cantidad respecto a otra. Existen muchas aplicaciones del concepto de razón
instantáneo y razón promedio tanto en Ingeniería, Economía, Física, Química, así como
también en Matemáticas. Son ejemplos, la razón de cambio del área de un círculo
respecto a su diámetro, la razón de cambio de la longitud de una varilla de metal
respecto a su temperatura, la razón de la solución de un compuesto químico en un
solvente respecto al tiempo así como por ejemplo, la cantidad de agua Q(lts) que hay en
un recipiente es función del tiempo t. Si el agua entra y sale, Q cambia en una cantidad
∆Q de un tiempo t a un tiempo t + ∆t . Entonces la razón de cambio media o promedio
de Q con respecto a t es:

∆Q dQ ∆Q
( lt / min ) y la razón instantánea: = lim ( 1t / min )
∆t dt ∆t →0 ∆t

Es decir, con frecuencia tales problemas pueden analizarse de una manera
completamente igual a la empleada para los problemas de la tangente y de la velocidad.
Así, si se dà y en términos de x por una fórmula y = f ( x) podemos discutir la razón de
cambio de y respecto a x.

Por razón de cambio de media de y respecto a x, desde x = x0 hasta x = x , se entiende
la relación:

14

f ( x) − f ( x0 ) cambio de ordenadas
=
x − x0 cambio de abscisas

Si el cociente diferencial tiene un límite cuando x → x0 , este límite está acorde con
nuestro concepto intuitivo de razón de cambio instantáneo de y con respecto a x.

Definición: La razón de cambio instantáneo de f ( x) respecto a x en x1 es la
derivada f ′ ( x1 ) siempre que la derivada exista.

Ejemplos:
1). Hallar la razón de cambio del área de un cuadrado respecto a un lado cuando el
lado mide 5 pulgadas.

Solución:
Sea A = f (a ) = a 2 , el área del cuadrado como función de su lado. Entonces:
Da A = f ′( a) = Da a 2 = 2a pu lg 2 / pu lg
a = 5 pu lg

⇒ Da A = 10 pu lg 2 / pu lg.
Todas las cantidades que se encuentran en la vida diaria cambian con el tiempo. Esto es
cierto especialmente en las investigaciones científicas. Por ejemplo, un químico puede
estar interesado en la cantidad de cierta substancia que se disuelve en el agua por unidad
de tiempo. Un ingeniero eléctrico puede querer saber qué tanto cambia la corriente en
alguna parte de un circuito eléctrico por unidad de tiempo. Un biólogo puede estudiar el
aumento (o la disminución), por unidad de tiempo, del número de bacterias de algún
cultivo. Pueden citarse muchos otros ejemplos, incluyendo algunos en campos fuera de
las ciencias naturales. Consideremos la siguiente situación que puede aplicarse a
cualquiera de los ejemplos anteriores.

Supongamos que una variable w es función del tiempo de manera que al tiempo t , w
está dada por w = g ( t ) , donde g es una función derivable. La diferencia entre el valor
inicial y el valor final de w en el intervalo de tiempo [ t , t + h] está dada por
g ( t + h ) − g (t ) . Análogamente a lo que hicimos tratamiento del concepto de velocidad,
formulamos la siguiente definición.

DEFINICIÒN

La razón media de cambio de w = g (t ) en el intervalo [ t , t + h ] es
g (t + h) − g (t )
h
La razón de cambio de w = g (t ) con respecto a t es

15

dw g (t + h) − g (t )
= g ′(t ) = lim
dt h →0 h

Las unidades que deben usarse en al definición (4.29) dependen de la naturaleza de la
cantidad representada por w . A veces dw / dt se llama la razón de cambio instantáneo
de w con respecto a t .

El límite de este cociente cuando h tiende a 0 (es decir, dy / dx ) se llama la razón de
cambio de y con respecto a x. Así, si la variable x cambia, entonces y cambia a razón
de dy / dx unidades por unidad de cambio de x. Por ejemplo, supongamos que cierta
cantidad de gas está encerrada en un globo. Si el gas se calienta o se enfría mientras la
presión permanece constante, el globo se dilata o se contrae y su volumen V es una
función de la temperatura t. La derivada dV / dT nos da la razón de cambio del
volumen con respecto a la temperatura.

16

PROBLEMAS PROPUESTOS
1.- La intensidad I (en amperes) de la corriente eléctrica en cierto circuito está dada
por I = 100 / R , donde R denota la resistencia (en ohms). Encuentre la razón de
cambio de I con respecto a R cuando la resistencia es 20 ohms.

2.- El radio (en centímetros) de un globo esférico que se está inflando, después de t
minutos está dado por r (t ) = 3 3 t + 8 , donde 0 ≤ t ≤ 10 . ¿Cuál es la razón de
cambio con respecto a t de cada una de las cantidades siguientes en t = 8? (a)
r(t) (b) el volumen del globo (c) El área de la superficie.
3.- Una escalera de 4 metros de largo está apoyada en una casa. Si el extremo
inferior se desliza por el suelo a razón de 1m/seg., ¿qué tan rápido cambia el
ángulo entre la escalera y el suelo cuando el extremo inferior está a 2 metros de
la casa?
4.- La iluminación I que produce una fuente de luz es directamente proporcional a
la intensidad S de la fuente e inversamente proporcional al cuadrado de la
distancia d a la fuente. Suponiendo que I es igual a 120 unidades a una distancia
de 2m, encuentre la razón de cambio de I con respecto a d a una distancia de
20m.
5.- Demuestre que la razón de cambio del radio de un círculo con respecto a su
perímetro es independiente del tamaño del círculo. Ilustre este hecho usando
unos círculos máximos sobre dos esferas, una del tamaño de un balón de
basketball y otra del de la tierra.
6.- La relación entre la temperatura F en la escala Fahrenheit y la temperatura C en
5
la escala Celsius está dada por C = ( F − 32). ¿Cuál es la razón de cambio de F
9
con respecto a C?.
7.- Un hombre sobre la azotea de un edificio, tira de una cuerda de 10 metros de
longitud en cuyo extremo esta atado un peso P. El hombre se aleja del borde de
la azotea con una velocidad de 2m/s ¿Con qué velocidad se alejan o se acercan el
hombre y el objeto en el instante en que ya el hombre ha caminado 3m?
8.- Un cilindro circular recto tiene una altura fija de 8cm. Hallar la razón de cambio
del volumen respecto al radio cuando este mide 2cm.
9.- Un estudiante de Ingeniería descubrió que el radio de una bola de nieve que se
derretía era de ( 4 − 0.04t ) pulgadas, donde t es el tiempo en minutos. Hallar la
razón de cambio del volumen respecto al tiempo al final de 1 hora.

10.- Hallar el punto (o los puntos) de la parábola y = x 2 + 2 x , donde la razón de
cambio de la pendiente de la normal respecto a x sea 2 por unidad de longitud.
11.- Hallar la variación respecto al tiempo del ángulo agudo formado por las
diagonales de un rectángulo si el lado mayor crece a razón de 4cm/seg., en una
dirección y el otro permanece constante igual a 10cm; en el instante en que el
lado que crece vale 17cm.

17

Datos: h = 10cm Dt b = 4cm / seg
se pide : Dt 0 = ?? cuando b = 17cm

12.- La longitud de una arteza horizontal es de 4m, su sección transversal es un
trapecio, el fondo tiene 2m de ancho; el seno del ángulo entre sus caras laterales
y el plano horizontal es 4/5. Se echa agua a la arteza a razón de 1/ 4m3 / min .
¿Con qué rapidez sube el nivel del agua, cuando el agua tiene 60cm de
profundidad.
13.- Un rombo tiene 10cms de lado. Dos de los vértices opuestos se separan a razón
de 2cm/seg. ¿Con qué rapidez cambia el área, en el momento en que los vértices
se han separado una distancia de 16 cms? (Tener en cuenta que los lados del
rombo tienen 10 cms en todo instante.

 x 2 + 3x ; x ≤ 1
14.- Un punto se mueve a lo largo de la curva: f ( x) =  De modo
 5x − 1 ; x > 1
que su abscisa cambie en la razón de 5 unidades por segundo. ¿Cuál es la razón
de cambio en su ordenada? ¿Cuánto vale esta razón en el instante en que pasa
por f ( x ) = 18 .

15.- Un punto móvil recorre con una velocidad de 3km/hr el diámetro vertical CB de
un círculo de centro 0, en el sentido de abajo arriba, partiendo de C. En el
extremo izquierdo A, del diámetro horizontal AD , hay un foco de luz, que
proyecta la sombra del punto móvil sobre el arco CDB. Calcular la velocidad de
dicha sombra en el momento en que el punto móvil ha recorrido la cuarta parte
de la longitud del diámetro.
16.- Una bola gira describiendo círculos en el extremo de una cuerda de 5 pies a una
velocidad de 20 r.p.m. Si la cuerda se rompe dejando escapar la bola
tangencialmente, ¿a qué velocidad se estará alejando del centro de su trayectoria
primitiva 1/100 de segundo después de que se rompió la cuerda?.
17.- Un hombre corre a lo largo de un diámetro de longitud 200mts. de un parque
semicircular, a una velocidad uniforme de 5m/seg. ¿A qué velocidad se moverá
su sombra a lo largo de la pared cuando los rayos del sol forman ángulo recto
con el diámetro.

18.- Un punto se mueve sobre la parábola 6 y = x 2 de manera que cuando x = 6 la
abscisa aumenta con una rapidez de 2mts/seg. ¿Con qué rapidez aumenta la
ordenada en ese instante?
19.- El piloto de un bombardero que vuela a 2kmts. De altura y a una velocidad de
240 km/hr, observa un blanco terrestre hacía el que se dirige. Calcular la
velocidad a la que debe girar el instrumento óptico cuando el ángulo entre la ruta
del avión y la línea de mira es 30º?

20.- El radio de la base de un cono aumenta a razón de 3cm/hr y la altura disminuye a
razón de 4cm/hr. Calcular como varía el área total del cono cuando el radio mide
7cm. Y la altura 24cm.

18

Aplicaciones de la derivada: recta tangente, máximos, mínimos y puntos de inflexión

Recomendados

Recomendados

Más contenido relacionado

La actualidad más candente

La actualidad más candente (20)

Destacado

Destacado (20)

Similar a Aplicaciones de la derivada: recta tangente, máximos, mínimos y puntos de inflexión

Similar a Aplicaciones de la derivada: recta tangente, máximos, mínimos y puntos de inflexión (20)

Aplicaciones de la derivada: recta tangente, máximos, mínimos y puntos de inflexión