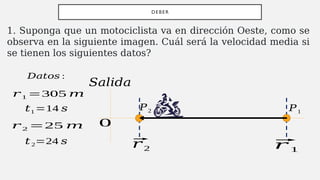
El documento explora los conceptos fundamentales de la cinemática, incluyendo tipos de movimiento y terminología asociada como sistema de referencia, desplazamiento, distancia, velocidad y aceleración. Se presentan ejemplos prácticos y ejercicios para entender cómo calcular la velocidad media y el desplazamiento en diferentes situaciones. También se describe el Movimiento Rectilíneo Uniforme (MRU) y el Movimiento Rectilíneo Uniformemente Variado (MRUV), proporcionando fórmulas y condiciones específicas para cada caso.