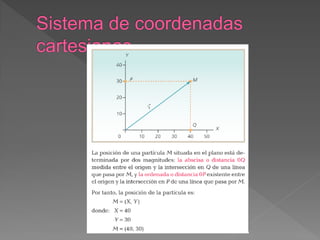
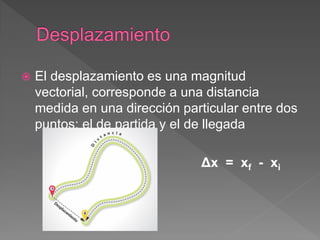
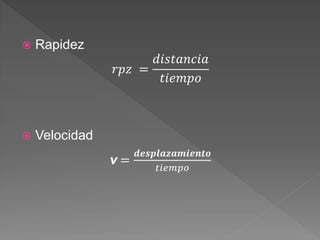
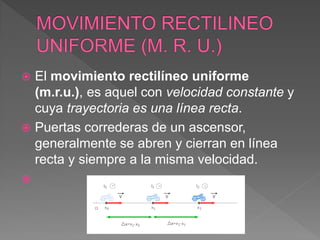
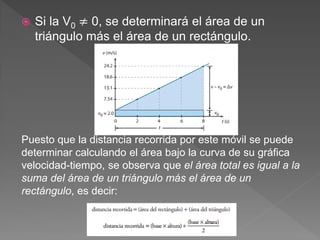
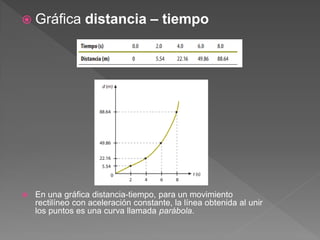
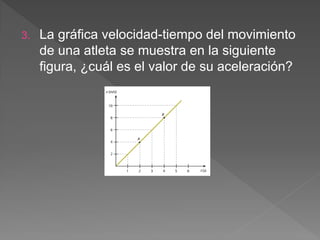
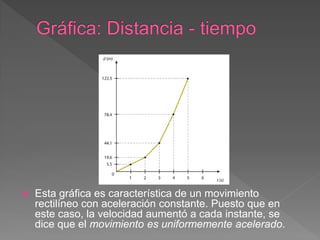
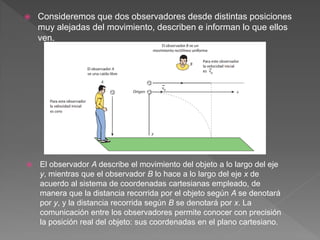
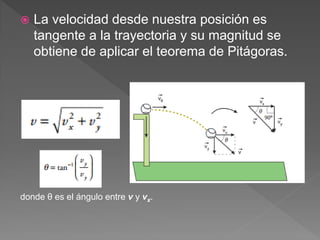
El documento define conceptos básicos de cinemática como movimiento, partícula, sistemas de referencia, trayectoria, distancia, desplazamiento, rapidez y velocidad. Explica que la cinemática estudia el movimiento de los cuerpos sin considerar las causas, mientras que la dinámica estudia las causas del movimiento.

2.  Cinemática: estudia los diferentes tipos de
movimiento de los cuerpos sin atender las
causas que lo producen.
 Dinámica: estudia las causas que originan
el movimiento de los cuerpos.
La estática que analiza las situaciones que
posibilitan el equilibrio de los cuerpos, queda
comprendida dentro del estudio de la dinámica.

3. CONCEPTOS BÁSICOS:
 Un cuerpo tiene movimiento cuando
cambia su posición a medida que transcurre
el tiempo. Fijar un sistema de referencia.
 Partícula: Cuerpo físico que es objeto de
estudio. (La Tierra, el sol, un avión, una
pelota, un electrón, etc.)

4.  Sistema de referencia absoluto: cuando
toma en cuenta un sistema fijo de referencia
(la Tierra). No existe.
 Sistema de referencia relativo: considera
móvil al sistema de referencia

6.  En una dimensión o sobre un eje (el
desplazamiento en línea recta de un
automóvil)
 En dos dimensiones o sobre un plano
(rueda de la fortuna, avión despegando,
proyectil)
 En tres dimensiones o en el espacio (un
tornillo perforando una pared

7.  Trayectoria: recorrido de una partícula
debido a su cambio de posición.
Dependiendo de su forma, puede ser:
› Rectilinea.
› Curvilínea.

8.  Cuando decimos que un cuerpo se encuentra
en movimiento, interpretamos que su posición
está variando respecto a un punto de
referencia.
 El estudio de la cinemática nos posibilita
conocer y predecir en qué lugar se encontrará
un cuerpo, qué velocidad tendrá al cabo de
cierto tiempo, o bien, en qué lapso llegará a su
destino. Hacer la descripción del movimiento
de un cuerpo significa precisar, a cada
instante, su posición en el espacio.

9.  La distancia recorrida por una partícula es una
magnitud escalar, ya que sólo interesa saber
cuál fue la magnitud de la longitud recorrida por
la misma durante su trayectoria seguida, sin
importar en qué dirección lo hizo.
 Por ejemplo: si a una persona le recomiendan
correr 3 km todos los días para tener buena
condición física, no importa si lo hace en línea
recta , o 1,5 km de ida y 1,5 de regreso, o
dando vueltas en un parte los 3 km.

10.  El desplazamiento es una magnitud
vectorial, corresponde a una distancia
medida en una dirección particular entre dos
puntos: el de partida y el de llegada
Δx = xf - xi

11.  Un nadador realiza un largo de pileta de 25
m, y luego vuelve a la posición de donde ha
salido.
› ¿Cuál es la distancia de ida?
› ¿Cuál es el desplazamiento de ida?
› ¿Cuál es la distancia de ida y vuelta?
› ¿Cuál es el desplazamiento de ida y vuelta?

12.  Rapidez: cantidad escalar que únicamente indica la
magnitud de la velocidad.
 Velocidad: magnitud vectorial, que requiere que se señale,
además de su magnitud, su dirección y su sentido.
Si la trayectoria es rectilínea, recorriendo distancias iguales
en cada unidad de tiempo, rapidez y velocidad permanecen
constantes.
Si una trayectoria es curvilínea, la rapidez puede ser
constante, pero la velocidad no, porque varía su sentido y/o
su dirección.

13.  La velocidad puede ser constante o variable.
 La velocidad se define como el
desplazamiento realizado por un móvil
divido entre el tiempo que tarda en
efectuarlo.

14.  Rapidez
𝑟𝑝𝑧 =
𝑑𝑖𝑠𝑡𝑎𝑛𝑐𝑖𝑎
𝑡𝑖𝑒𝑚𝑝𝑜
 Velocidad
v =
𝒅𝒆𝒔𝒑𝒍𝒂𝒛𝒂𝒎𝒊𝒆𝒏𝒕𝒐
𝑡𝑖𝑒𝑚𝑝𝑜

15.  Un corredor avanza 3 km en un tiempo de 10
minutos. Calcular su rapidez en Km/h y en m/s.
 La rapidez de un ciclista es de 10 m/s. ¿Qué
distancia recorre en 125 s?
 ¿Cuál es la velocidad en m/s de un motociclista
cuyo desplazamiento es de 8 km al este en 9
minutos?
 Determinar el desplazamiento en metros que
realizará un automóvil al viajar hacia el norte a una
velocidad de 80 km/h durante 0,9 minutos.
 Una lancha de motor desarrolla una velocidad cuya
magnitud es de 6,5 m/s, si la velocidad que lleva la
corriente de un río hacia el este es de 3,4 m/s,

16.  El movimiento rectilíneo uniforme
(m.r.u.), es aquel con velocidad constante y
cuya trayectoria es una línea recta.
 Puertas correderas de un ascensor,
generalmente se abren y cierran en línea
recta y siempre a la misma velocidad.


17. Un movimiento rectilíneo uniforme (m.r.u.) es
aquel que tiene su velocidad constante y su
trayectoria es una línea recta. Esto implica
que:
 El espacio recorrido es igual que el
desplazamiento.
 En tiempos iguales se recorren distancias
iguales.
 La rapidez o celeridad es siempre constante
y coincide con el módulo de la velocidad.

18.  Velocidad
En los m.r.u. la velocidad del cuerpo es constante y por tanto
igual a la velocidad inicial. Su unidad en el Sistema
Internacional (S.I.) es el metro por segundo (m/s).
𝒗 = 𝒗𝟎= cte
𝒗 = 𝜟𝒅
𝜟𝒕
donde:
› v es la velocidad.
› v0 es la velocidad inicial.

20.  Posición
Su unidad en el Sistema Internacional (S.I.) es el
metro (m) y se obtiene por medio de la siguiente
expresión:
donde:
 𝒙 = 𝒙𝟎 + 𝒗𝒕
› x0 es la posición inicial.
› v es la velocidad que tiene el cuerpo a lo largo del
movimiento.
› t es el intervalo de tiempo durante el cual se mueve el
cuerpo.
Observación: a veces es representado por t y otras por ∆t.
En cualquiera de los casos, t=∆t = tf - ti siendo tf y ti los
instantes de tiempo final e inicial respectivamente del
movimiento que estamos estudiando.

21. Existe una relación
de proporcionalidad
directa entre variable
desplazamiento y la
variable tiempo.
Para calcular la
magnitud de la
velocidad, basta
determinar la
tangente de la recta.

23.  Analizar la gráfica y calcular el espacio
recorrido a partir de ella.

24.  Analizar la gráfica y calcular la velocidad a
partir de ella.

25.  Con los datos de la magnitud del
desplazamiento de un móvil en función del
tiempo, se obtuvo la siguiente gráfica:
 Interpretar la información que brinda.

27.  José y Lucas acordaron ir a la plaza a andar en
bicicleta a las 15 h. Lucas fue puntual y se
sentó en una sombra a esperar a su amigo. A
las 15:15, José rápidamente toma su bicicleta y
se dirige a la plaza a una velocidad constante
de 10 m/s.
Lucas, cansado de esperar, al mismo tiempo se
sube a su bicicleta y se dirige a la casa de José,
que se encuentra a 300 m de distancia, a una
velocidad de 5 m/s. ¿Cuánto tiempo tardan en
encontrarse, a qué distancia de la plaza lo hacen?

28.  Un colectivo parte de Puerto Rico hacia
Buenos Aires a las 20:00 h, con una rapidez
de 90 km/h. Un auto parte del mismo origen,
con el mismo destino, a las 23:00 h y con
una rapidez de 144 Km/h. ¿A cuánto tiempo
de viaje del colectivo el coche lo cruzará?
¿En qué lugar?

29.  Un coche se mueve a una velocidad
constante de 20 m/s. Transcurridos 10
segundos sale en su persecución un
patrullero en la misma dirección y sentido
con una velocidad de 30 m/s. ¿Cuánto
tiempo tardaran en encontrarse? ¿A qué
distancia lo harán?.

30.  Definir MRUA.
 Dar ejemplos de este tipo de movimiento
que se observen en la vida cotidiana.
 Explicar las características del MRUA.

31. Un cuerpo realiza un movimiento rectilíneo
uniformemente acelerado
(m.r.u.a.) o movimiento rectilíneo
uniformemente variado
(m.r.u.v.) cuando su trayectoria es una línea
recta y su aceleración es constante.
Esto implica que la velocidad aumenta o
disminuye su módulo de manera uniforme.

32.  Es el cambio de velocidad con respecto al tiempo.
 Matemáticamente la aceleración se expresa por:
𝒂 =
∆𝒗
∆𝑡
 𝒂 =
𝒗 −𝒗𝟎
𝑡 −𝑡0
donde:
› a→ = aceleración
› Δv → = cambio de velocidad
› Δt = intervalo de tiempo
El cambio de velocidad Δv se define como la diferencia entre la velocidad final y la
velocidad inicial del móvil.
Es decir:
Δv → = v – v0 o Δv = vf – vi
donde:
› vf = v = velocidad final
› vi = v0 = velocidad inicial

33.  La aceleración es una magnitud vectorial que tiene
la misma dirección y el mismo sentido que el
cambio de velocidad.
 La unidad de aceleración es una unidad de
velocidad dividida por una unidad de tiempo.
Por tanto, la unidad de aceleración es una
unidad de longitud dividida entre una unidad de
tiempo al cuadrado, o sea m/s2 en el Sistema
Internacional.

34. Un ejemplo de este tipo de movimiento se presenta cuando
un autobús inicia su movimiento a lo largo de una carretera
recta partiendo del reposo (v0 = 0 m/s) e incrementa el valor
de su velocidad uniformemente.
Los valores que marca el velocímetro del autobús cada 2
segundos durante los primeros 8 segundos se presentan en
la siguiente tabla.
La aceleración de este autobús es constante y se obtiene
de tomar un par de valores de la tabla, es decir:

35.  Al ser la aceleración del autobús constante,
la gráfica de la aceleración con función del
tiempo (gráfica aceleración - tiempo) es
una línea recta horizontal que indica que la
aceleración no cambia

36.  Gráfica velocidad-tiempo
 La velocidad no es constante, sino directamente proporcional al
tiempo que transcurre, o sea que los cambios en la magnitud de la
velocidad son los mismos para iguales intervalos de tiempo, por
eso se obtiene una línea recta inclinada.
 En una gráfica de velocidad-tiempo, la pendiente de la curva en
cada punto es igual a la magnitud de la aceleración del
movimiento.
 El área bajo la curva de la gráfica velocidad-tiempo en el intervalo
de interés es igual a la distancia recorrida por el móvil. Si la V0 = 0,
Se determinará el área de un triángulo (base por altura dividida
entre dos)

37.  Si la V0 = 0, se determinará el área de un
triángulo.

38.  Si la V0 ≠ 0, se determinará el área de un
triángulo más el área de un rectángulo.
Puesto que la distancia recorrida por este móvil se puede
determinar calculando el área bajo la curva de su gráfica
velocidad-tiempo, se observa que el área total es igual a la
suma del área de un triángulo más el área de un
rectángulo, es decir:

39.  Gráfica distancia – tiempo
 En una gráfica distancia-tiempo, para un movimiento
rectilíneo con aceleración constante, la línea obtenida al unir
los puntos es una curva llamada parábola.

40.  𝒂 =
∆𝒗
∆𝑡
 𝒂 =
𝒗 −𝒗𝟎
𝑡 −𝑡0
sí t0 = 0s 𝒂 =
𝒗 −𝒗𝟎
𝑡
 𝒗 = 𝒗𝟎 + 𝒂𝒕
 x = 𝒗𝟎𝒕 +
𝟏
𝟐
𝒂𝒕𝟐
 𝟐𝒂∆𝒙 = 𝒗𝒇
𝟐 − 𝒗𝒊
2

41.  Una moto que se mueve a 20 m/s, aumenta
su valor de velocidad a 25 m/s en 5 s, ¿cuál
es su aceleración?
 Este valor indica que la moto aumenta el
valor de su velocidad en 1 m/s cada
segundo.

42.  Si la moto que se movía a 25 m/s disminuye su valor de
velocidad a 15 m/s, en 5 s, tendrá un valor de aceleración
igual a:
 Este valor indica que la magnitud de la velocidad
disminuyó a un ritmo de 2 m/s cada segundo.
 De acuerdo con estos resultados, el término aceleración
se aplica a qué tan deprisa aumenta o disminuye la
velocidad en un cierto tiempo. Los frenos de un auto
pueden producir una gran disminución por segundo del
valor de la velocidad. A menudo a esto se le conoce como
desaceleración o aceleración negativa.

43. 1. Un automóvil en una carretera recta acelera
de 2.18 m/s a 16.66 m/s en 8.0 s ¿cuál es
el valor de aceleración en dicho intervalo?
2. Un automóvil de carreras partió del reposo
con una aceleración de 6 m/s2, ¿cuál será
el valor de su velocidad (rapidez) después
de 10 s? El auto se mueve a lo largo de una
carretera recta.

44. 3. La gráfica velocidad-tiempo del movimiento
de una atleta se muestra en la siguiente
figura, ¿cuál es el valor de su aceleración?

45. ¿Cuántos
aceleradores
tiene un auto?

46. 4. Un camión parte del reposo y acelera de forma tal
que en 10 s logra una distancia de 100 m. ¿Qué
aceleración ha tenido el vehículo?.
5. Un avión con sus motores a máxima potencia
comienza a carretear por la pista hasta lograr una
velocidad de 360 km/h. La longitud de la pista es de
1000 m. Calcular la aceleración.
6. Un citroen pasa de 36 km/h a 72 km/h en 2 minutos.
Calcular la aceleración en /s y en km/h.
7. Un automóvil parte del semáforo y a los 10 s alcanza
una velocidad de 108 km/h. Calcular el espacio
recorrido y la aceleración.
8. Un camión viaja en una carretera recta a 22.5 m/s
(81 km/h) y frena con una aceleración constante de
2.27 m/s2. ¿Cuánto viaja antes de detenerse?

47.  Es un movimiento rectilíneo con aceleración
constante.
 Un cuerpo en caída libre es definido como un
cuerpo que se mueve a partir del reposo bajo la
acción de la gravedad en un lugar en donde la
resistencia del aire es despreciable.
 Ejemplo: cuando una moneda se deja caer al piso
o cuando una fruta madura se cae del árbol

48.  Aristóteles y sus seguidores afirmaban que
los cuerpos caían debido a que su lugar
natural era el piso y que hacían todo lo
posible por llegar a él.
 También sostenían que los cuerpos más
pesados deberían llegar antes al
piso que los cuerpos ligeros, cuando se
soltaban simultáneamente desde la misma
altura.

49.  Galileo identificó a la caída libre de los
cuerpos como un movimiento rectilíneo
vertical con aceleración constante, por lo
que todos los cuerpos en ausencia de aire
caerán al mismo tiempo si se sueltan desde
la misma altura.

50.  A esta aceleración se le conoce como
aceleración de la gravedad y se le
representa por la letra g.
 Su magnitud al nivel del mar es de 9.8 m/s2 ,
su dirección es vertical con sentido hacia
abajo (centro de la Tierra).
 El valor de g en la Tierra varía según la
altitud y la región en donde se mida.

51.  El valor de g en la Tierra varía según la
altitud y la región en donde se mida.
 Indagar por qué ocurre esto.

52.  En 1971, el astronauta David Scott soltó
simultáneamente una pluma y un martillo en
la Luna, desde la misma altura y observó
que los dos cuerpos llegaban al mismo
tiempo a la superficie lunar.
 Hay que señalar que en la Luna no hay
atmósfera y por lo tanto, tampoco resistencia
en la caída de los cuerpos

53.  Esta gráfica es característica de un movimiento
rectilíneo con aceleración constante. Puesto que en
este caso, la velocidad aumentó a cada instante, se
dice que el movimiento es uniformemente acelerado.

54. 

55.  Convenciones:
Se tomará como positivo el sentido del
movimiento cuando el cuerpo se mueve hacia
abajo; o sea, que las velocidades y
desplazamientos serán también positivos.

56. 1. Una persona se cae de una tabla que cruza
por encima de un arroyo y golpea el agua 1.2 s
después. ¿Cuál es la altura de la tabla sobre el
arroyo?
2. Un ladrillo suelto cae al piso de la calle desde
la azotea de un edifcio de 50 m de altura.
a) ¿Cuál es el valor de la velocidad con que
se impacta contra el piso?
b) ¿Cuánto tiempo tardará en caer?

57. 3. Una pelota se deja caer desde la azotea de un edificio. Si
tarda 4 s en caer, ¿cuál es la altura del edificio?
4. Desde lo alto de una torre de 40 m se deja caer un
objeto.
a) ¿Con qué velocidad se impactará en el piso?
b) ¿Cuánto tiempo tardará en caer dicho objeto?
5. Una cubeta se deja caer en un pozo. Si tarda en caer 1.0
s.
a) ¿Cuál es la profundidad del pozo?
b) ¿Con qué velocidad se impactará
en el fondo?

58.  Movimiento vertical bajo la aceleración de la
gravedad.
 Cuando un cuerpo cae o asciende una
distancia relativamente corta, el movimiento es
uniformemente acelerado.
 La aceleración es la misma para todos los
cuerpos, (tanto en caída como en ascenso), se
denota con g y se conoce como aceleración de
la gravedad.
 Estas afirmaciones son correctas siempre que
sea posible despreciar la resistencia del aire
(se aplica a cuerpos compactos).

59.  Fenómeno que se presenta cuando se lanza un
objeto verticalmente hacia arriba observándose
que su velocidad va disminuyendo hasta
anularse al alcanzar su altura máxima.
 El tiro vertical es un movimiento sujeto a la
aceleración gravitacional de forma que la
aceleración se opone al movimiento inicial del
objeto lanzado.
La aceleración de la gravedad,
provoca que el objeto del tiro
vertical vaya perdiendo velocidad
hasta llegar al estado de reposo y
seguidamente a partir de ese
punto, comienza un movimiento
de caída libre con su velocidad
inicial nula.

60.  La velocidad inicial nunca es igual a cero.
 Cuando el objeto en movimiento alcanza su
máxima altura, la velocidad en ese punto es
cero. Mientras el objeto se encuentra en
movimiento de subida, su velocidad es
positiva y cuando el objeto desciende su
velocidad es negativa.
 El tiempo de subida y de bajada son iguales.

61. 9,81 m/s2
- 9,81 m/s2

62.  Movimiento de caída libre causado
exclusivamente por la aceleración de la
gravedad  vi=0.
 Tiro Vertical: La velocidad inicial
siempre es diferente de cero  vi<> 0
• En ambos casos el movimiento es
rectilíneo uniformemente variado
(MRUV) con a = g

63. Ecuaciones MRUV
o MRUA
 𝒂 =
𝒗 −𝒗𝟎
𝑡
 𝒗 = 𝒗𝟎 + 𝒂𝒕
 xf = 𝑿𝒊 + 𝒗𝟎𝒕 +
𝟏
𝟐
𝒂𝒕𝟐
 𝟐𝒂∆𝒙 = 𝒗𝒇
𝟐 − 𝒗𝒊
2
Ecuaciones en tiro vertical y
caída libre
 g =
𝒗 −𝒗𝟎
𝑡
 𝒗 = 𝒗𝟎 + 𝒈𝒕
 hf = 𝒉𝒊 + 𝒗𝟎𝒕 +
𝟏
𝟐
𝒈𝒕𝟐
 𝟐𝒈∆𝒉 = 𝒗𝒇
𝟐 − 𝒗𝒊
2
 ℎ max =
𝑣𝑖
2
2𝑔

66. 1. Una partícula se lanza en la dirección vertical con una velocidad
inicial de 90 Km/h. Calcular la altura máxima que alcanzará.
2. Un niño lanza una piedra hacia arriba con una velocidad inicial de
15.5 m/s. Calcular la altura máxima que alcanza la piedra antes de
comenzar a descender.
3. ¿Con qué velocidad inicial se debe disparar una flecha verticalmente
hacia arriba para que alcance una altura máxima de 130 m?
4. ¿Cuánto tardará la flecha del ejemplo anterior en alcanzar dicha
altura máxima?
5. Se lanza una pelota verticalmente hacia arriba con una velocidad de
8 m/s. Determina su altura máxima, y el tiempo que demora en
alcanzarla
6. Calcula el tiempo que demora un cuerpo en llegar al suelo si se
lanza verticalmente hacia arriba desde el piso con una velocidad de
30 m/s
7. Una cancha de paddle tiene un techo de 10 metros de altura. Al
terminar un partido el ganador, entusiasmado, arroja su paleta hacia
arriba con una velocidad de 20 m/s . ¿Alcanza a golpear el techo?

67.  Es el desplazamiento realizado por cualquier
objeto cuya trayectoria describe
una parábola
 Es un ejemplo de un movimiento realizado
por un objeto en dos dimensiones o sobre
un plano.
 Puede considerarse como la combinación de
dos movimientos que son un movimiento
horizontal uniforme y un movimiento vertical.

68.  Proyectil: cualquier cuerpo u objeto que
arrojado mediante un impulso
continúa en movimiento en virtud de su inercia
y de la aceleración de la gravedad.
 En este movimiento, la aceleración es
constante y perpendicular a la dirección de la
velocidad inicial, debido a que la aceleración a
la que están sometidos, es la aceleración de la
gravedad.

69.  La aceleración es constante y
perpendicular a dirección de la
velocidad inicial. Es decir, la
aceleración y la velocidad del
cuerpo en el tiro horizontal no
tienen la misma dirección.

70.  Consideremos que dos observadores desde distintas posiciones
muy alejadas del movimiento, describen e informan lo que ellos
ven.
 El observador A describe el movimiento del objeto a lo largo del eje
y, mientras que el observador B lo hace a lo largo del eje x de
acuerdo al sistema de coordenadas cartesianas empleado, de
manera que la distancia recorrida por el objeto según A se denotará
por y, y la distancia recorrida según B se denotará por x. La
comunicación entre los observadores permite conocer con precisión
la posición real del objeto: sus coordenadas en el plano cartesiano.

72.  Para conocer la distancia que hay entre el
objeto y el origen del sistema de
coordenadas (magnitud del vector de
posición) se utiliza ….
 El teorema de Pitágoras

73.  La velocidad medida por el observador B se
denotará por vx y las velocidades inicial y
final, para cualquier instante, vistas por A, se
denotarán por v0y y vy respectivamente.

74.  La velocidad desde nuestra posición es
tangente a la trayectoria y su magnitud se
obtiene de aplicar el teorema de Pitágoras.
donde θ es el ángulo entre v y vx.

75.  La aceleración en el movimiento

76.  Si se toman dos esferas iguales mantenidas
al mismo nivel y una de ellas se deja caer
mientras que la otra es impulsada
horizontalmente, las dos llegarán al piso al
mismo tiempo.

77.  Una pelota es arrojada de modo horizontal con
una rapidez de 30 m/s desde un edificio de 20
m de altura. ¿Cuánto tiempo emplea —desde
que se arrojó— en tocar el piso?
 Una esfera de acero se arroja horizontalmente
a 30.0 m/s desde lo alto de un edificio de 50.0
m de altura.
› a) ¿A qué distancia de la base del edificio caerá la
esfera de acero?,
› b) ¿Cuál es la magnitud de la velocidad con que se
impacta la esfera de acero en el piso?