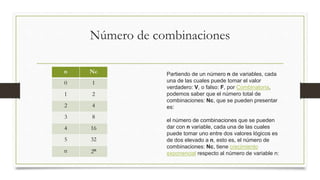
Este documento explica qué son las tablas de verdad y cómo se usan para demostrar la función de los operadores lógicos. Describe los operadores lógicos principales como AND, OR, NOT e implicación y cómo se definen sus valores de verdad en tablas. También cubre conceptos como disyunción, conjunción, equivalencia y el número de combinaciones posibles en tablas de verdad con base en el número de variables.

1. Centro de Estudios Tecnológicos industrial y de
servicio N°109
Francisco Ruiz Luis Eduardo
Espinosa Alba Karen Michelle
Tablas de Verdad para C++
MAESTRA: MARGARITA ROMERO
ALVARADO

2. ¿Qué es una tabla de verdad?
Las tablas de verdad es una estrategia de la lógica simple que permite
establecer la validez de varias propuestas en cuanto a cualquier situación, es
decir, determina las condiciones necesarias para que sea verdadero un
enunciado propuesto, permitiendo clasificarlos en tautológicos (resultan
verdaderos durante cualquier situación) contradictorias (son enunciados falsos
en la mayoría de los casos) o contingentes (enunciados que no pueden será
tantos verdaderos como falsos no existen tendencia a un solo sentido).

3. Tablas de verdad
Las tablas de verdad nos permiten demostrar la función de un operador lógico en todas sus posibles
variaciones o combinaciones.
La tabla de verdad esta compuesta por una o mas variables (por lo general 2) y los operadores lógicos
con los que se quiera combinar.

4. Operadores Lógicos
Nombre: Simból
icamen
te
Descripción
Y ^ Indica que todas las proposiciones deben ser verdaderas para que el resultado sea
verdadero, de lo contrario será falso.
O v Indica que una o varias de las proposiciones debe ser verdadera para que el resultado
sea verdadero. Si todas las proposiciones son falsas, el resultado es falso.
Implicación o
Entonces
=> Ejemplo: Si hoy es lunes entonces mañana es martes.
O Exclusivo o
Excluyente
Ô Indica que solo una de las variables puede ser verdadera para que el resultado sea
verdadero, si hay mas variables verdaderas el resultado es falso.
En otras palabras, solo se puede elegir una cosa y no varias.
Doble Implicación o
Bidireccional
<=> Indica que las todas las proposiciones deben ser o verdaderas o falsas para que el
resultado sea verdadero, de lo contrario el resultado es falso.
No
¬ Indica que se debe escribir el inverso de un resultado.
Por ejemplo:
P = V
¬ P = F

5. Disyunción
• La disyunción es un operador
lógico que actúa sobre dos valores
de verdad, típicamente los valores
de verdad de dos proposiciones,
devolviendo el valor de
verdad verdadero cuando una de las
proposiciones es verdadera, o
cuando ambas lo son, y falso cuando
ambas son falsas.

6. Variable
• Para una variable lógica A, B, C, ...
pueden ser verdaderas V, o falsas F,
los operadores fundamentales se
definen así:
A A
V V
F F

7. Negación
• La negación operador que se
ejecuta, sobre un único valor de
verdad, devolviendo el
valor contradictorio de la
proposición considerada.
A ~A
V F
F V

8. Conjunción
• La conjunción es un operador, que
actúa sobre dos valores de verdad,
típicamente los valores de verdad
de dos proposiciones, devolviendo
el valor de verdad verdadero cuando
ambas proposiciones son
verdaderas, y falso en cualquier otro
caso. Es decir, es verdadera cuando
ambas son verdaderas
A B A^B
V V V
V F F
F V F
F F F

9. Implicación o Condicional
• El condicional material es un
operador que actúa sobre dos
valores de verdad, típicamente los
valores de verdad de dos
proposiciones, devolviendo el valor
de falso sólo cuando la primera
proposición es verdadera y la
segunda falsa, y verdadero en
cualquier otro caso.
A B A=>B
V V V
V F F
F V V
F F V

10. Equivalencia, doble implicación o Bicondicional
• El bicondicional o doble
implicación es un operador que
funciona dando el valor de verdad
cuando ambos valores son iguales y
dando el valor de falsedad cuando
ambos valores son diferentes.
A B AB
V V V
V F F
F V F
F F V

11. Número de combinaciones
n Nc
0 1
1 2
2 4
3 8
4 16
5 32
n 2ⁿ
Partiendo de un número n de variables, cada
una de las cuales puede tomar el valor
verdadero: V, o falso: F, por Combinatoria,
podemos saber que el número total de
combinaciones: Nc, que se pueden presentar
es:
el número de combinaciones que se pueden
dar con n variable, cada una de las cuales
puede tomar uno entre dos valores lógicos es
de dos elevado a n, esto es, el número de
combinaciones: Nc, tiene crecimiento
exponencial respecto al número de variable n:

12. Bibliografía
https://sites.google.com/site/lordsionlsyk/informatica/operadores-logicos-tablas-de-verdad-valores-
de-verdad
https://es.wikipedia.org/wiki/Tabla_de_verdad