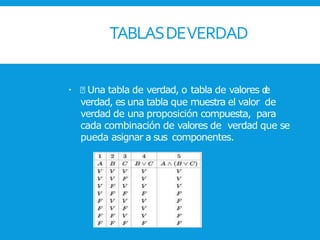
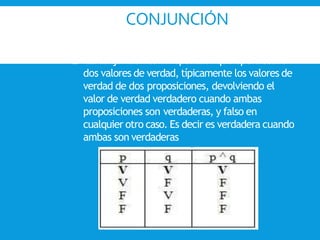
El documento explica los conceptos básicos de las tablas de verdad y las operaciones lógicas. Define valores de verdad, disyunción, conjunción, negación, condicional y bicondicional. Proporciona ejemplos de cada operación lógica y sus tablas de verdad correspondientes. Finalmente, concluye que una tabla de verdad muestra el valor de verdad de un enunciado compuesto para todas sus posibles interpretaciones.

1. *VICTOR YAEL NAVA MARTINEZ
*KARLA LORENA SALDAÑA PEREZ

3. TABLASDEVERDAD
 Una tabla de verdad, o tabla de valores de
verdad, es una tabla que muestra el valor de
verdad de una proposición compuesta, para
cada combinación de valores de verdad que se
pueda asignar a sus componentes.

4. VALORESDEVERDAD
Losvalores de verdad posibles son
dos: verdadero y falso,pueden expresarse
como 1 y0.
Normalmente serepresenta al valor Verdadero
con la letra Vy al valor Falsocon la F.También se
usan las letras T(por “true”, “verdadero” en
inglés) y F(por “false”, “falso” eninglés).

5. DISYUNCIÓN
p q p∨q
V V V
V F V
FF VV VV
FF FF FF
Ladisyunción es un operador que opera
sobre dos valores de verdad,
típicamente losvalores de verdad de dos
proposiciones, devolviendo el valor de
verdad verdadero cuando una de las
proposiciones es verdadera, o cuando
ambas lo son, y falso cuando ambas son
falsas.

6. EJEMPLOS
p v q (selee: ” p o q”)
1# p =” Elnumero 2espar”
q =” la sumade 2 +2 es4″
entonces…
pvq: “El numero 2 espar o la sumade 2 +2 es4″
2# p =” Laraíz cuadrada del 4es2”
q =” Elnumero 3 espar″
entonces…
pvq: “La raízcuadrada del 4 es 2 o el numero 3 espar”

7. CONJUNCIÓN
La conjunción es un operador que opera sobre
dos valores de verdad, típicamente los valores de
verdad de dos proposiciones, devolviendo el
valor de verdad verdadero cuando ambas
proposiciones son verdaderas, y falso en
cualquier otro caso. Es decir es verdadera cuando
ambas son verdaderas

8. EJEMPLOS
p ^ q (se lee: ” p y q”)
1# p = ” El numero 4 es par”
q = ”Siempre el residuo de los números pares es 2″
entonces…
p^q: “El numero 4 es par y Siempre el residuo de
los números pares es 2″
2# p = ” El numero mas grande es el 34”
q = ”El triangulo tiene 3 lados″
entonces…
p^q: “El numero mas grande es el 34 y El triangulo
tiene 3 lados”

9. NEGACIÓN
Lacaracterística de la negación esque
invierte el valor de verdad de la
proposición. Lanegaciónes
un operador que seejecuta sobre un
único valor de verdad, devolviendo el
valor contradictorio de la proposición
considerada. Consiste en cambiar el valor
de verdad de una variable proposicional.
p
V F
F V
¬p
V
VV

10. EJEMPLOS
1# p: “4 + 4 es igual a 9”
-p: “4 + 4 no es igual a 9″
2# p: “El 4 es un numero par”
-p: “El 4 no es un numero par”

11. p q p⇒q
VV VV VV
VV FF FF
F V V
F F V
CONDICIONAL
Elcondicional material esun operador
que opera sobre dos valores de verdad,
típicamente los valores de verdad dedos
proposiciones, devolviendo el valor de
verdad falso sólo cuando la primera
proposición esverdadera y la segunda
falsa, y verdadero en cualquier otro
caso.
Lacondicionalde dos proposiciones p, q
da lugar ala proposición; si p entonces
q, serepresenta por p→q

12. EJEMPLOS
1# p: “llueve”
q: “hay nubes”
p→q: “si llueve entonces hay nubes”
2# p: “Hoy es miércoles”
q: “Mañana será jueves”
p→q: “Si Hoy es miércoles entonces Mañana
será jueves”

13. p q p⇔q
V V V
VV FF FF
FF VV FF
FF FF VV
BICONDICIONAL
Elbicondicional o doble implicación es
un operador que funciona sobre dos
valores de verdad, típicamente los
valores de verdad de dos
proposiciones, devolviendo el valorde
verdad verdadero cuando ambas
proposiciones tienen el mismo valor
de verdad, y falso cuando susvalores
de verdad difieren.

14. EJEMPLOS
1# p: “10 es un número impar”
q: “6 es un número primo”
p↔q: “10 es un número impar si y solo si 6 es
un número primo”
2# p: “3 + 2 = 7”
q: “4 + 4 = 8”
p↔q: “3 + 2 = 7 si y solo si 4 + 4 = 8″

15. PROPOSICIÓN
Una proposición sólo puede ostentar uno de
ellos (ni los dos a la vez, ni ninguno de ellos).
Estosvalores sellaman “booleanos”
Una proposición esuna afirmación capazde
tener un valor de verdad. Esdecir, una oración
de la cual sepuede decir que esverdadera o que
esfalsa.

16. OPERACIONES
LÓGICAS
Unaoperación lógica secompone de operandos
(proposiciones) y operadores. Mediante una
operación lógica seunen proposiciones para obtener
una nueva proposición compuesta.
Losoperadores lógicos (también llamados
“conectores lógicos”) usadospara unir proposiciones
son:AND(“y”), OR(“o”), NOT(“no”), IMPLICA,
BICONDICIONAL(“si y sólo si”). Mediante ellos se
forman proposiciones moleculares.

17. OPERACIONES
LÓGICAS
Eloperador ORserepresenta mediante el símbolo∨
y seutiliza para la operación disyunción.
Eloperador NOTserepresenta mediante el símbolo ¬
y seutiliza para la operación negación.
Eloperador IMPLICAserepresenta mediante el
símbolo ⇒ y seusaparala
operación implicaciónoperador sela llama
“antecedente” y ala que secoloca ala derecha de la
llama “consecuente“. Estaoperación no es
conmutativa.

18. OPERACIONES
LÓGICAS
Eloperador BICONDICIONALserepresenta mediante
el símbolo ⇔ y seusapara la operación doble
implicación(también llamada “equivalencia“).
Lanegación esuna operación unaria, porque
involucra un único operando (proposición). Elresto
son binarias, porque involucran dosoperandos.
Además, pueden unirse másde dos proposiciones,
usando másde un operador lógico.

19. TABLADEVERDADDE
CADA
 Lógicosunenlosoperadoresproposiciones.Entonces,al unir dos
proposiciones,seobtiene unanuevaproposición, cuyovalordeverdad
dependerádecuálesson concretamentelosvaloresdeverdaddelas
proposiciones unidas
 Las tablas de las operaciones, de acuerdo a las distintas posibles
combinaciones de los valores de verdad de los operandos, son las
siguientes:
operador lógico
p q p∧q

20. EQUIVALENCIAS
LOGICAS
Una equivalencia lógica esuna similitud en grados de verdad
existen entre 2 o masexpresiones, siendo cualquiera de ellas
validas; esdecir cualquiera de estaspuede ser usadaen la
demostración de un sujeto, sin que ello implique variación en el
resultado final por el cambio o sustitución de cualquiera deellas.
Lademostración de equivalencias mascomúnmente usadaes
mediante el método de tablas deverdad.

21. FORMANORMACONJUNTIVAATRAVÉSDE
MANIPULACIONESALGEBRAICAS
1._Eliminar todas las‘’y’’
2._Sila expresión contiene cualquiera sobrexpresión compuesta
negada elimínela.
3._Una vezencontrada una expresión sin ninguna sobrexpresión
compuesta negada, uselas 2 leyes siguientes para reducir el
alcance de V.

22. CONCLUSIÓN
Podemos concluir que una tabla de verdad
de un enunciado (molecular) muestra el
valor de verdad de dicho enunciado para
todas las posibles combinaciones de los
valores de verdad de las proposiciones que
lo componen, o de manera más breve, una
tabla de verdad de un enunciado muestra
el valor de verdad de dicho enunciado para
todas sus interpretaciones.

23. OPINIÓN
No P yQ
V F =F
V V =V
F F = V
F V =F
Siuna de las proposiciones es Falsa, yla otra Verdadera,
entonces el resultado es Falso. Silas dos proposiciones son
Verdaderas o Falsas (siempre ambas), el resultado es
Verdadero.

24. REFERENCIA
solocodigo.com ›Foros ›Programación General › C/C++
https://mx.answers.yahoo.com/question/index?qid=200911
27161257AAHkApE
www.portalhacker.net/index.php/topic,109660.5/wap2.html