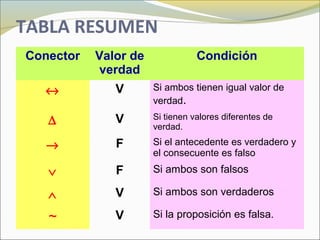
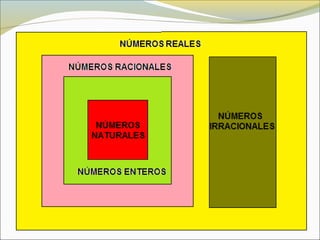
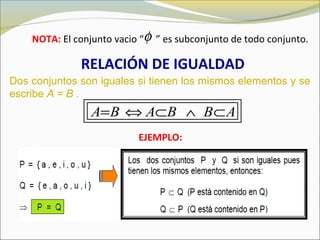
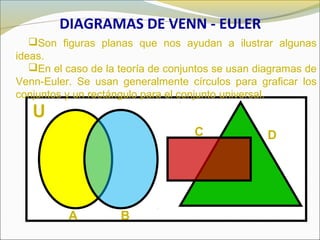
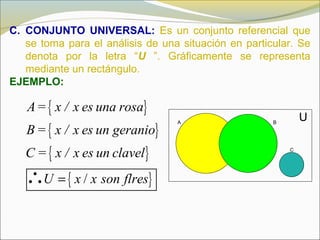
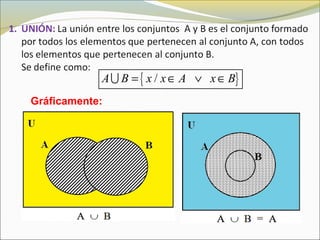
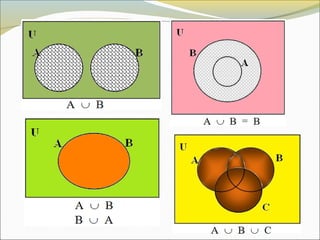
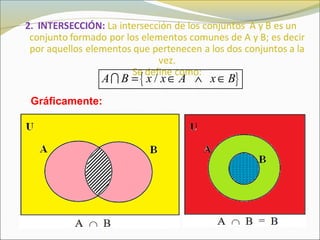
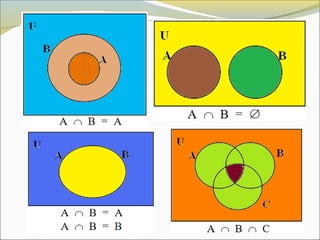
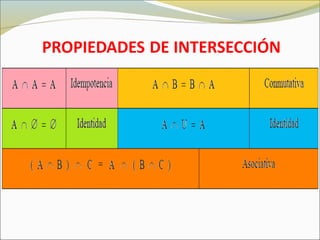
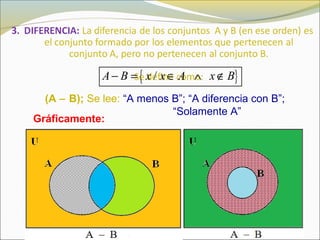
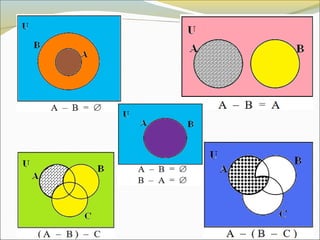
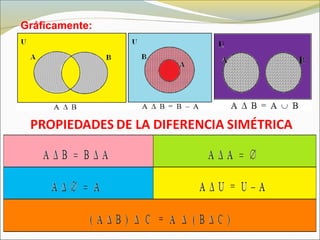
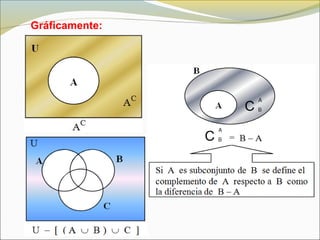
El documento define conceptos básicos de lógica y conjuntos. Explica que un conjunto es una colección bien definida de objetos con características en común. Los elementos de un conjunto pueden ser reales, abstractos o imaginarios. También introduce la notación estándar para representar conjuntos y sus elementos. Finalmente, presenta ejemplos de conjuntos numéricos.