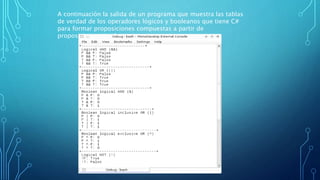
El documento describe las tablas de verdad para operadores lógicos en C++. Explica que las tablas de verdad muestran los resultados de aplicar operadores lógicos a proposiciones simples y cómo están formadas por filas y columnas. Además, provee ejemplos de conjunción, disyunción y condicionales.

1. TABLAS DE VERDAD PARA
C++

2. Centros de Estudios Tecnologicos y de Servicios Cetis 109
2 Dm Programacion
Ibarra Sanchez Melany Itzel
Estrella Cruz Rogelio Abrahan
Mta.Margarita Romero Alvarado

3. TABLAS DE VERDAD CON OPERADORES
• El método más general para analizar los valores de verdad de las
proposiciones compuestas es escribirlas en forma de una tabla. En estas
tablas básicas de verdad se puede saber rápidamente si una proposición
compuesta es verdadera o falsa, ya que muestra los resultados obtenidos
al aplicar cada uno de los operadores lógicos, así como el resultado de la
proposición de cada uno de los valores que puedan tener las diferentes
proposiciones simples que integran una proposición compuesta.
na tabla de verdad esta formada por filas y columnas, donde el número de filas
depende de los posibles valores de verdad para cada proposición simple, mientras
que el número de columnas depende del número de proposiciones simples que
integran la proposición compuesta más el número de operadores lógicos que las
conecten.

4. EJEMPLO:
EN DONDE N ES EL NÚMERO DE PROPOSICIONES DIFERENTES QUE
INTEGRAN UNA PROPOSICIÓN COMPUESTA Y M ES EL NÚMERO DE
POSIBLES VALORES DE VERDAD PARA CADA PROPOSICIÓN.

5. A continuación la salida de un programa que muestra las tablas
de verdad de los operadores lógicos y booleanos que tiene C#
para formar proposiciones compuestas a partir de
proposiciones simples.

6. DEFINICIONES
Se pueden definir otras, como se hace en la lógica de circuito
siempre y cuando se le encuentre un sentido lógico pertinente. Por
eso puede haber diversos sistemas de cálculo según las funciones
que se definan.
Por otro lado algunas funciones pueden definirse como
combinación de otras. Por ejemplo la función A → B es equivalente
a la función combinada ¬(A /¬ B), como puede comprobarse
haciendo la tabla de verdad. Este tipo de equivalencias son muy
útiles para el establecimiento de reglas para el cálculo deductivo,
pues al ser equivalencias suponen una tautología, como ley lógica.

7. FUNCIONES DE
VERDAD
Consiste en cambiar el valor de verdad de una variable
proposicional.

8. CONJUCION
La proposición molecular será verdadera sólo cuando
ambas variables proposicionales sean verdaderas

9. DISYUNCION
La proposición molecular será verdadera cuando
una o ambas variables proposicionales sean
verdaderas

10. CONDICIONAL
La proposición molecular será verdadera cuando se cumpla
si es verdadero A entonces lo es B.

11. BIBLIOGRAFIAS
https://tutoborlandudis.es.tl/Tablas-de-verdad.htm
http://xomalli.blogspot.mx/2017/01/tablas-de-verdad-de-
operadores-logicos.html