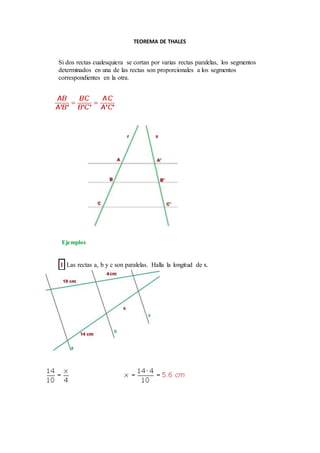
El documento explica el Teorema de Tales, el cual establece que si dos rectas son cortadas por varias rectas paralelas, los segmentos determinados en una de las rectas son proporcionales a los segmentos correspondientes en la otra recta. También se aplica este teorema en triángulos, donde si se traza una recta paralela a uno de los lados, los lados del nuevo triángulo formado serán proporcionales a los del triángulo original. Finalmente, se presentan algunos ejemplos para ilustrar cómo aplicar este te

1. TEOREMA DE THALES
Si dos rectas cualesquiera se cortan por varias rectas paralelas, los segmentos
determinados en una de las rectas son proporcionales a los segmentos
correspondientes en la otra.
Ejemplos
1 Las rectas a, b y c son paralelas. Halla la longitud de x.

2. 2 Las rectas a, b son paralelas. ¿Podemos afirmar que c es paralela a las rectas
a y b?
Sí, porque se cumple el teorema de Thales.
Teorema de Thales en un triángulo
Dado un triángulo ABC, si se traza un segmento paralelo, B'C', a uno de
los lados del triangulo, se obtiene otro triángulo AB'C',
cuyos lados son proporcionales a los del triángulo ABC.

3. Ejemplo:
Hallar las medidas de los segmentos a y b.
Señala la opción correcta:
1Dos figuras semejante s tienen...
el mis mo tamaño y distinta forma.
la mis ma forma y sus tamaños pueden ser proporc iona les.
el mis mo tamaño y forma aunque pueden variar en determina da s
oc asiones.
2Dada una figura c ualquiera podemos c onstruir otra semejante a
ella...

4. ampliándo la, es dec ir "hac iéndo la más grande".
Reduc iéndo la, es dec ir "hac iéndo la más pequeña ".
Las dos respuestas anteriores son c orrec tas.
3Entre los lados de dos figuras semejante s...
Sólo hay una variac ión de tamaño sin c ondic iones.
Existe una razón de proporc io na lida d llamada razón de semejanza o
esc ala.
Existe una razón de proporc io na lida d llamada c oc iente de semejanza .
4Si un segmento de 10 c m de longitud es semejante a otro de 5
c m, entonc es...
la razón de semejanza es k = 2.
la razón de semejanza se k = 3.
el c oc iente de semejanza es k = 2.

5. 5Un triángulo de lados 5 c m, 12 c m y 13 c m es semejante a otro
triángulo de lados...
7.5 c m, 18 c m, 19.5 c m.
7.5 c m, 18.5 c m, 19.5 c m.
15 c m, 36 c m, 49 c m.
6La razón de proporc io na lida d de los triángulos del ejerc ic io
anterior es...
k = 2.5.
k = 1.5.
k = 3.
7Si tenemos un c uadrado de lado 2.5 c m y hac emos otro
semejante a él aplic ando una razón de proporc io na lida d k = 2 el
lado del nuevo c uadrado será de...
5 c m.

6. 1.5 c m.
3 c m.
8Dado un segmento de 20 c m, c onstruimo s otro semejante a él
aplic ando una esc ala k = 0.2. Dic ho segmento medirá...
2 c m.
10 c m.
4 c m.
9Debido a la razón de proporc io na lida d, dos figuras semeja ntes...
Pueden deforma rse.
Pueden ser de distinto tamaño pero no se deforma n una respec to de
la otra.
Son exac tamente las mis mas.
10En dos figuras semejantes.. .
Los puntos, lados y ángulos c orrespondientes se dic en homólo gos.

7. los puntos y ángulos c orrespondie ntes se dic en homólogos.
los lados y ángulos c orrespondie ntes se dic en homólo gos .
Señala la opción correcta:
1Para poder aplic ar el teorema de T hales nec esitamos. ..
dos rec tas c ualesquie ra y varias rec tas paralelas entre sí que c orten a
las anteriores.
dos rec tas paralelas y varias rec tas c ualesquie ra que c ortan a las
anteriores.
dos rec tas c ualesquie ra y varias rec tas paralelas entre sí que pueden
serlo o no a las anteriores.
2Una de las aplic ac iones del teorema de T hales es...
dividir un segmento en varias partes iguales.
formar un segmento a partir de varias de sus partes.

8. Las dos respuestas anteriores son c orrec tas.
3Podemo s aplic ar el teorema de T hales en triángulos c uando...
trazamos rec tas paralelas a alguno de sus lados.
trazamos rec tas perpendic ula res a alguno de sus lados.
trazamos rec tas paralelas a alguno de sus lados que interseque n a los
otros dos lados del mis mo.
4Sabiendo que las rec tas r, s y t son paralelas, la longitud de x
es
2.5 c m
3 c m.
No se puede c alc ular.

9. 5Sabiendo que las rec tas r, s y t son paralelas, las longitudes
que faltan son:
x = 2.625 c m, y = 10 c m.
x = 10 c m, y = 2.625 c m.
Faltan datos para resolver el proble ma .
6Sean a y b dos rec tas c ualesquie ra y r y s dos rec tas que las
c ortan. Si los segmentos que determina n a y bson m = 5.5, n =
4, m' = 2.5 y n' = 2 entonc es...
r y s son paralelas .
r y s no son paralela s.
r y s son perpendic ula res .

10. 7Sabiendo que el segmento DE es paralelo a la base del
triángulo, las medidas de los segmentos a y b son...
a = 8 c m y b = 10 c m.
a = 9 c m y b = 11 c m.
Ninguna de las respuestas anteriores es c orrec ta.
8Sabiendo que los segmentos que mide n 3 c m y 4 c m son
paralelos , c alc ular a y b.
a = 3 c m y b = 0.5 c m.

11. a = 3 c m y b = 1.6 c m.
a = 3.5 c m y b = 0.6 c m.
Resuelve los siguientes problemas:
9¿Cuál es la altura del montón de libros situado sobre el
c ésped?
c m
10Observa ndo la esc alera que aparec e en el dibujo c alc ula
la longitud de la c uerda que une los peldaños de la
esc alera c on su parte posterior.
c m