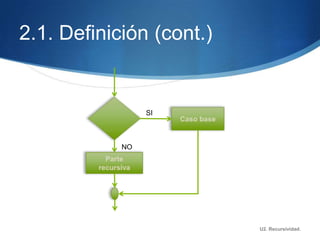
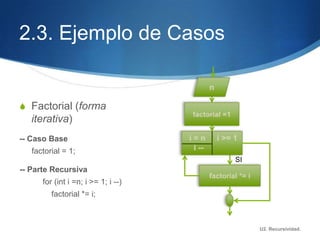
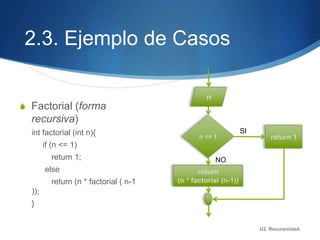
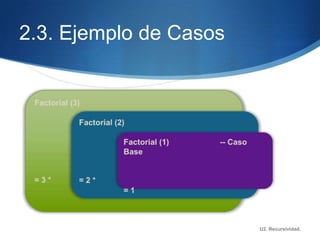
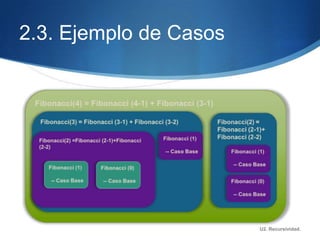
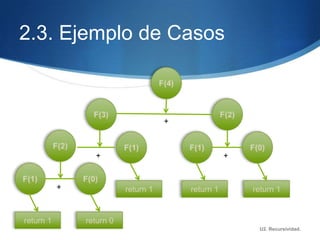
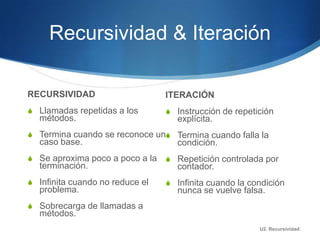
Este documento describe la recursividad, incluyendo su definición, tipos de procedimientos recursivos y ejemplos como el factorial, Fibonacci, triángulo de Pascal. La recursividad se basa en la llamada repetida de un método dentro de su propia definición hasta alcanzar un caso base. Ofrece ventajas como menos líneas de código pero también desventajas como un mayor uso de memoria y tiempo de procesamiento.

1. Estructura de Datos
2. Recursividad.
http://www.informatik.uni-trier.de/~naeher/Professur/
S

2. Contenido
2.1. Definición
2.2. Procedimientos recursivos
2.3. Ejemplos de casos
U2. Recursividad.

3. http://codificando-sin-control.blogspot.com/2010/06/la-recursividad.html
2. Recursividad
S
U2. Recursividad.

4. 2.1. Definición
Alternativa diferente para implementar estructuras de
repetición (ciclos). Se apoya en la modularidad, pues a
través de los módulos se hacen llamadas recursivas.
Un módulo es recursivo si, como parte de su
definición, incluye al menos una llamada a sí mismo
(Martínez, R. & Quiroga, E., 2001)
U2. Recursividad.

5. 2.1. Definición (cont.)
A recursive definition is one that refers to the object it is
defining as part of its definition.
“A bouquet of roses one rose, or two roses, or three
roses, …”
(Decker, H., 1993)
U2. Recursividad.

6. 2.1. Definición (cont.)
Un método recursivo es un método que se llama así
mismo, ya sea directa o indirectamente, a través de
otro método.
(Deitel, H. M. & Deitel P. J., 2004)
Un método parcialmente definido en términos de sí
mismo, ya sea directa o indirectamente, a través de
otro método.
(Weiss, M. A)
U2. Recursividad.

7. 2.1. Definición (cont.)
SI
NO
U2. Recursividad.

8. 2.2. Procedimientos
Recursivos
S TIPOS:
S Recursión simple
S Recursión múltiple
S Recursión cruzada o indirecta
S Recursión anidada
U2. Recursividad.

9. 2.3. Ejemplo de Casos
S FACTORIAL
S ¿Cómo se calcula el factorial de un número?
S Ejemplo:
S 0!, 1!, 2!, 3!, 4!, 5!
U2. Recursividad.

10. 2.3. Ejemplo de Casos
S Factorial (forma
iterativa)
-- Caso Base
factorial = 1;
SI
-- Parte Recursiva
for (int i =n; i >= 1; i --)
factorial *= i;
U2. Recursividad.

11. 2.3. Ejemplo de Casos
S Factorial (forma
recursiva)
int factorial (int n){ SI
if (n <= 1)
return 1; NO
else
return (n * factorial ( n-1
));
}
U2. Recursividad.

12. Ejercicio
S Encuentre el error en el siguiente método recursivo
y explique cómo corregirlo:
public int suma(int n)
{
if (n == 0)
return 0;
else
return n + suma (n);
}
U2. Recursividad.

13. 2.3. Ejemplo de Casos
U2. Recursividad.

14. 2.3. Ejemplo de Casos
U2. Recursividad.

15. 2.3. Ejemplo de Casos
U2. Recursividad.

16. 2.3. Ejemplo de Casos
U2. Recursividad.

17. 2.3. Ejemplo de Casos
U2. Recursividad.

18. 2.3. Ejemplo de Casos
U2. Recursividad.

19. U2. Recursividad.

20. 2.3. Ejemplos de casos
S FIBONACCI (Leonardo de Pisa)
S ¿Cómo se calcula la serie Fibonacci?
U2. Recursividad.

21. 2.3. Ejemplos de casos
S FIBONACCI (Leonardo de Pisa)
S ¿Cómo se calcula la serie Fibonacci?
S Condiciones:
S Fibonacci (0) = 0 n=0
S Fibonacci (1) = 1 n=1
S Fibonacci (n) = Fibonacci(n-1)+Fibonacci(n-2) n>1
U2. Recursividad.

22. 2.3. Ejemplo de Casos
U2. Recursividad.

23. 2.3. Ejemplo de Casos
+
+ +
+
U2. Recursividad.

24. 2.3. Ejemplos de casos
Triángulo de Pascal
1
11
121
1331
14641
…
U2. Recursividad.

25. 2.3. Ejemplos de casos
TRIÁNGULO DE PASCAL
int comb(int n, int m)
{
if ((n == 0) || (n == m))
return 1;
else
return comb(n-1,m-1) + comb(n-1,m);
}
U2. Recursividad.

26. Práctica (Equipo)
S De los siguientes problemas resueltos de forma
iterativa, encontrar su solución recursiva mediante
codificación:
1. Fibonacci (n-1) + (n-2)
2. Conversión de un número decimal a binario (n/2, n%2)
3. Potencia (base, exponente)
U2. Recursividad.

27. Práctica (Equipo)
Fibonacci
int Fibonacci (int n){
//Casos Base
if (n == 0)
return 0;
else{
if (n == 1)
return 1;
// Paso recursivo
else{
return Fibonacci(n-1)+Fibonacci(n-2);
}
}
}
U2. Recursividad.

28. Práctica (Equipo)
Conversión Decimal a Binario
void aBinario (int n){
// Paso recursivo
if (n >= 2)
aBinario (n/2);
System.out.print(n%2);
}
U2. Recursividad.

29. Práctica (Equipo)
Elevar a una potencia
int Potencia (int n, int exp){
//Casos Base
if (exp == 0)
return 1;
else{
if (exp == 1)
return n;
// Paso recursivo
else{
return n * Potencia(n, exp-1);
}
}
}
U2. Recursividad.

30. Recursividad & Iteración
RECURSIVIDAD ITERACIÓN
S Llamadas repetidas a los S Instrucción de repetición
métodos. explícita.
S Termina cuando se reconoce unS Termina cuando falla la
caso base. condición.
S Se aproxima poco a poco a la S Repetición controlada por
terminación. contador.
S Infinita cuando no reduce el S Infinita cuando la condición
problema. nunca se vuelve falsa.
S Sobrecarga de llamadas a
métodos.
U2. Recursividad.

31. Ventajas
S Menos líneas de código.
S Refleja el problema con más naturalidad.
S Produce un programa más fácil de entender y depurar.
U2. Recursividad.

32. Desventajas
S Tiempo de procesador.
S Espacio en memoria, consume memoria adicional.
U2. Recursividad.

33. Referencias
1. Martínez, R. & Quiroga, E. (2001). Estructura de datos.
Referencia práctica con orientación a objetos. Thomson
Learning.
2. Decker, H. (1993). Working Classes. Data Structures and
algorithms using C++. PWS Publishing Company.
3. Deitel, H. M. & Deitel P. J. (2004). Cómo programar en JAVA
5ª Edición. Pearson Hall.
4. Weiss, M. A. Estructura de datos en Java. Ed. Addison
Wesley.
U2. Recursividad.

34. ¡ Gracias por su atención !
www.tecmartinez.edu.mx
Tel y Fax: (232) 3.73.52.40 . CP 93600
Miguel Hidalgo # 101, Col. Adolfo Ruiz Cortínez . Martínez de la Torre, Veracruz, México.
34