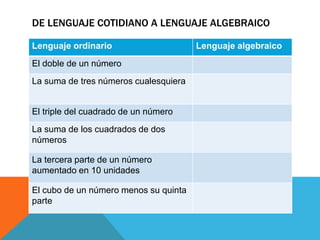
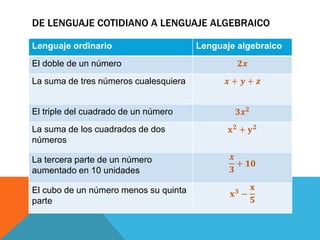
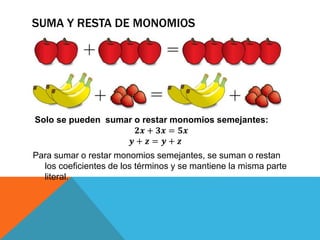
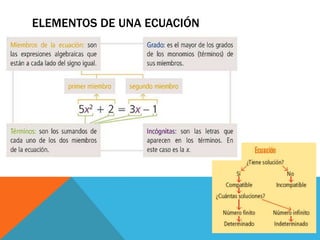
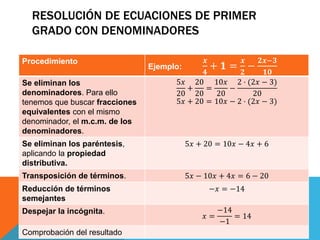
El documento describe el lenguaje algebraico y cómo se utilizan letras y símbolos para expresar relaciones matemáticas de manera abstracta. Explica cómo expresiones cotidianas se pueden convertir a lenguaje algebraico y define términos como monomios, polinomios y ecuaciones. Además, proporciona procedimientos para resolver ecuaciones de primer grado.

2. LENGUAJE ALGEBRAICO
El lenguaje algebraico es aquel que se sirve de letras, números y
signos de operaciones para expresar informaciones matemáticas.

3. DE LENGUAJE COTIDIANO A LENGUAJE ALGEBRAICO
Lenguaje ordinario Lenguaje algebraico
El doble de un número
La suma de tres números cualesquiera
El triple del cuadrado de un número
La suma de los cuadrados de dos
números
La tercera parte de un número
aumentado en 10 unidades
El cubo de un número menos su quinta
parte

4. DE LENGUAJE COTIDIANO A LENGUAJE ALGEBRAICO
Lenguaje ordinario Lenguaje algebraico
El doble de un número 𝟐𝒙
La suma de tres números cualesquiera 𝒙 + 𝒚 + 𝒛
El triple del cuadrado de un número 𝟑𝒙 𝟐
La suma de los cuadrados de dos
números
𝐱 𝟐 + 𝐲 𝟐
La tercera parte de un número
aumentado en 10 unidades
𝒙
𝟑
+ 𝟏𝟎
El cubo de un número menos su quinta
parte
𝐱 𝟑 −
𝐱
𝟓

5. EXPRESIONES ALGEBRAICAS
Una expresión algebraica es una expresión matemática en
la que se combinan letras y números unidos por los signos de
las operaciones aritméticas, suma, resta, multiplicación,
división y potenciación.

6. VALOR NUMÉRICO DE UNA EXPRESIÓN ALGEBRAICA
Las incógnitas representan los valores desconocidos o
indeterminados de las expresiones algebraicas.
El valor numérico de una expresión algebraica es el número
que se obtiene al sustituir las incógnitas o letras por valores
determinados y hacer las operaciones indicadas en la expresión.
Ejemplo: Mi padre me lleva 25 años. Si yo tengo x años, mi padre
tendrá x + 20.
• Cuando yo tenga 15 años, mi padre tendrá 15 + 25 = 40
• Cuando yo tenga 32 años, mi padre tendrá 32 + 25 = 57

7. MONOMIOS
Los monomios son las expresiones algebraicas más
sencillas: tienen un solo término. Están formadas por el
producto de un número, llamado coeficiente, y una o varias
letras, llamada parte literal. El grado de un monomio es la
suma de los exponentes de la parte literal.
−2𝑥4 es un monomio de grado 4
6𝑥3
𝑦2
es un monomio de grado 5
Dos monomios son semejantes si
tienen la misma parte literal.

8. POLINOMIOS
Los polinomios son expresiones algebraicas compuestas
por la suma o la resta de varios monomios.

9. SUMA Y RESTA DE MONOMIOS
Solo se pueden sumar o restar monomios semejantes:
𝟐𝒙 + 𝟑𝒙 = 𝟓𝒙
𝒚 + 𝒛 = 𝒚 + 𝒛
Para sumar o restar monomios semejantes, se suman o restan
los coeficientes de los términos y se mantiene la misma parte
literal.

10. MULTIPLICACIÓN DE MONOMIOS

12. DIVISIÓN DE MONOMIOS

13. ECUACIONES
DETECTIVES EN BÚSQUEDA DE LA SOLUCIÓN
http://www.educaplus.org/play-13-Ecuaciones-visuales.html

14. IGUALDADES, IDENTIDADES Y ECUACIONES
Una igualdad es una expresión con dos miembros separados
por un signo igual
• Una identidad es una igualdad algebraica que es cierta
para cualquier valor de sus letras.
• Una ecuación es una igualdad algebraica que es cierta
solo para ciertos valores de sus letras.

15. ELEMENTOS DE UNA ECUACIÓN

16. ¿Cuánto vale x?

17. RESOLUCIÓN DE ECUACIONES DE PRIMER
GRADO SENCILLAS
Procedimiento Ejemplo: 𝟔𝒙 + 𝟑 − 𝟐𝒙 = 𝒙 + 𝟗
Transposición de términos: Se
pasan a un miembro los términos con
incógnita y a otro los términos
numéricos. Si cambian de miembro,
cambian de signo.
6𝑥 − 2𝑥 − 𝑥 = 9 − 3
Reducción de términos semejantes 3𝑥 = 6
Despejar la incógnita: El coeficiente
que multiplica a la incógnita, pasa al
otro miembro, dividiendo.
𝑥 =
6
3
= 2
Comprobación del resultado 6 · 2 + 3 − 2 · 2 = 2 + 9
12 + 3 − 4 = 11
15 − 4 = 11
11 = 11

18. RESOLUCIÓN DE ECUACIONES DE PRIMER
GRADO CON PARÉNTESIS
Procedimiento Ejemplo: 𝟑 · 𝟐𝒙 − 𝟏 + 𝟓 = 𝟕𝒙 − 𝟒 · (𝒙 −
𝟐)
Se eliminan los paréntesis,
aplicando la propiedad
distributiva.
6𝑥 − 3 + 5 = 7𝑥 − 4𝑥 + 8
Transposición de términos. 6𝑥 − 7𝑥 + 4𝑥 = 8 + 3 − 5
Reducción de términos
semejantes
3𝑥 = 6
Despejar la incógnita.
𝑥 =
6
3
= 2
Comprobación del resultado 3 · 2 · 2 − 1 + 5 = 7 · 2 − 4 · (2 − 2)
3 · 4 − 1 + 5 = 14 − 4 · 0
3 · 3 + 5 = 14 + 0
9 + 5 = 14
14 = 14

19. RESOLUCIÓN DE ECUACIONES DE PRIMER
GRADO CON DENOMINADORES
Procedimiento
Ejemplo:
𝒙
𝟒
+ 𝟏 =
𝒙
𝟐
−
𝟐𝒙−𝟑
𝟏𝟎
Se eliminan los
denominadores. Para ello
tenemos que buscar fracciones
equivalentes con el mismo
denominador, el m.c.m. de los
denominadores.
5𝑥
20
+
20
20
=
10𝑥
20
−
2 · (2𝑥 − 3)
20
5𝑥 + 20 = 10𝑥 − 2 · (2𝑥 − 3)
Se eliminan los paréntesis,
aplicando la propiedad
distributiva.
5𝑥 + 20 = 10𝑥 − 4𝑥 + 6
Transposición de términos. 5𝑥 − 10𝑥 + 4𝑥 = 6 − 20
Reducción de términos
semejantes
−𝑥 = −14
Despejar la incógnita.
𝑥 =
−14
−1
= 14
Comprobación del resultado