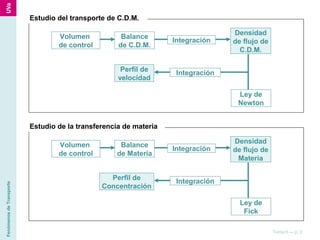
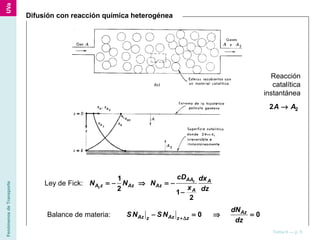
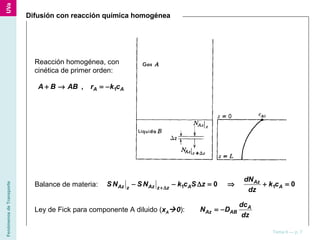
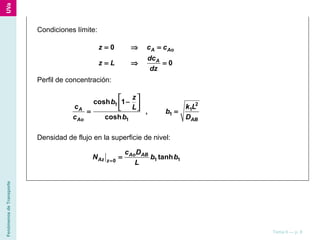
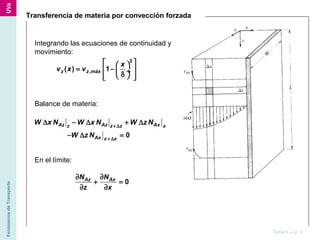
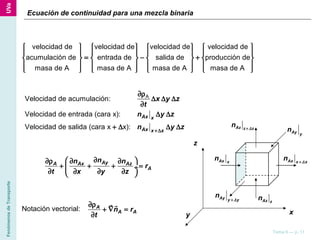
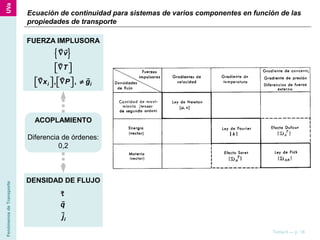
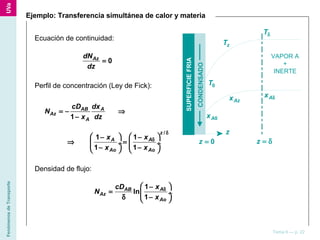
El documento describe diferentes ecuaciones y modelos matemáticos para analizar el transporte de materia en sistemas con varios componentes, incluyendo ecuaciones de continuidad, leyes de Fick, y modelos para difusión simple, difusión con reacción química, y transferencia de materia por convección. También discute cómo estas ecuaciones se aplican a coordenadas rectangulares, cilíndricas y esféricas.

1. FenómenosdeTransporte
Tema 6 — p. 1
TEMA 6
Ecuaciones de variación para sistemas de varios
componentes
Balances de materia aplicados a una envoltura: condiciones límite:
Difusión a través de una película gaseosa estancada
Difusión con reacción química heterogénea
Difusión con reacción química homogénea
Transferencia de materia por convección forzada
Ecuación de continuidad para una mezcla binaria: La ecuación de
continuidad en diversos sistemas coordenados
Ecuación de continuidad para sistemas de varios componentes en
función de las densidades de flujo
Ecuación de continuidad para sistemas de varios componentes en
función de las propiedades de transporte
Ejemplo: Transferencia simultánea de calor y materia

2. FenómenosdeTransporte
Tema 6 — p. 2
Ley de
Newton
Perfil de
velocidad
Integración
Balance
de C.D.M.
Volumen
de control
Integración
Densidad
de flujo de
C.D.M.
Estudio del transporte de C.D.M.
Ley de
Fick
Perfil de
Concentración
Integración
Balance
de Materia
Volumen
de control
Integración
Densidad
de flujo de
Materia
Estudio de la transferencia de materia

3. FenómenosdeTransporte
Tema 6 — p. 3
Balances de materia aplicados a una envoltura: condiciones límite
velocidad de velocidad de velocidad de
entrada de salida de producción de
materia de A materia de A materia de A
0
     
     
− + =     
     
     
Balance de materia en régimen estacionario
( )A
Az AB A Az Bz
x
N cD x N N
z
∂
= − + +
∂
Ley de Fick
• Concentración conocida: xA= xAo
• Densidad de flujo conocida: NA= NAo
• Transporte de interfase sólido-fluido: NAz= kc(cA-cAo)
Condiciones límite habituales

4. FenómenosdeTransporte
Tema 6 — p. 4
Difusión a través de una película gaseosa estancada
Ley de Fick:
0
1
AB A
Bz Az
A
cD x
N N
x z
∂
= ⇒ = −
− ∂
Balance de materia:
0Az Azz z z
SN SN +∆
− = ⇒ 0AzdN
dz
=
Condiciones límite:
1 1
2 2
o
A
A A
T
A A
P
z z x x
P
z z x x
= ⇒ = =
= ⇒ =
Perfil de concentración:
1
2 1
2
1 1
1 1
1 1
z z
z z
A A
A A
x x
x x
 −
 ÷
−    − −
= ÷  ÷
− −   
Densidad de flujo:
2
2 1 1
lnAB B
Az
B
cD x
N
z z x
=
−

5. FenómenosdeTransporte
Tema 6 — p. 5
Difusión con reacción química heterogénea
Reacción
catalítica
instantánea
22A A→
Ley de Fick: 2
2
1
2
1
2
AA A
A z Az Az
A
cD dx
N N N
x dz
= − ⇒ = −
−
Balance de materia: 0 0Az
Az Azz z z
dN
SN SN
dz+∆
− = ⇒ =

6. FenómenosdeTransporte
Tema 6 — p. 6
Condiciones límite:
0
0
A Ao
A
z x x
z x
= ⇒ =
= δ ⇒ =
Perfil de concentración:
1
1 1
2 2
z
AoA xx
−
δ  
− = − ÷  ÷
   
Densidad de flujo:
2
2 1
ln
1
2
AA
Az
Ao
cD
N
x
=
δ
−

7. FenómenosdeTransporte
Tema 6 — p. 7
Difusión con reacción química homogénea
Reacción homogénea, con
cinética de primer orden:
1, A AA B AB r k c+ → = −
Balance de materia: 1 10 0Az
Az Az A Az z z
dN
SN SN k c S z k c
dz+∆
− − ∆ = ⇒ + =
Ley de Fick para componente A diluido (xA0): A
Az AB
dc
N D
dz
= −

8. FenómenosdeTransporte
Tema 6 — p. 8
Condiciones límite:
0
0
A Ao
A
z c c
dc
z L
dz
= ⇒ =
= ⇒ =
Perfil de concentración:
21
1
1
1
cosh 1
,
cosh
A
Ao AB
z
b
c k LL
b
c b D
 
−  = =
Densidad de flujo en la superficie de nivel:
1 10
tanhAo AB
Az z
c D
N b b
L=
=

9. FenómenosdeTransporte
Tema 6 — p. 9
Transferencia de materia por convección forzada
Integrando las ecuaciones de continuidad y
movimiento:
2
,( ) 1z z máx
x
v x v
  
= −  ÷
δ   
Balance de materia:
0
Az Az Axz z z x
Ax x x
W x N W x N W z N
W z N
+∆
+∆
∆ − ∆ + ∆
− ∆ =
En el límite:
0Az AxN N
z x
∂ ∂
+ =
∂ ∂

10. FenómenosdeTransporte
Tema 6 — p. 10
Ley de Fick:
( ) ( ) ( )
( )
A
Az AB A Az Bz A Az Bz A z
A A
Ax AB A Ax Bx AB
dc
N D x N N x N N c v x
dz
dc dc
N D x N N D
dx dx
= − + + ≈ + ≈
= − + + ≈ −
Substituyendo:
2 2
, 2
1 A A
z máx AB
c cx
v D
z x
  ∂ ∂ 
− =  ÷
δ ∂ ∂   
Condiciones límite:
0 0
0
0
A
A Ao
A
z c
x c c
c
x
x
= ⇒ =
= ⇒ =
∂
= δ ⇒ =
∂
La solución:
,
4
A
Ao AB
z máx
c x
erfc
c D z
v
=

11. FenómenosdeTransporte
Tema 6 — p. 11
Ecuación de continuidad para una mezcla binaria
z
xy
Ax x
n Ax x x
n + ∆
Az z
n
Az z z
n + ∆
Ay y
n
Ay y y
n
+ ∆
velocidad de velocidad de velocidad de velocidad de
acumulación de entrada de salida de producción de
masa de A masa de A masa de A masa de A
       
       
= − +       
       
       
Ax x
Ax x x
x y z
t
n y z
n y z+∆
∂ρ
∆ ∆ ∆
∂
∆ ∆
+ ∆ ∆ ∆
A
Velocidad de acumulación:
Velocidad de entrada (cara x):
Velocidad de salida (cara x x):
AyA Ax Az
A
nn n
r
t x y z
∂ ∂ρ ∂ ∂
+ + + = ÷
∂ ∂ ∂ ∂ 
Notación vectorial: A
A An r
t
∂ρ
+ ∇ =
∂
r r

12. FenómenosdeTransporte
Tema 6 — p. 12
Análogamente para el componente B: B
B Bn r
t
∂ρ
+ ∇ =
∂
r r
Sumando las dos ecuaciones:
0
A B
A B
A B
n n n v
r r
ρ + ρ = ρ 

+ = = ρ ⇒
+ = 
r r r r
· 0v
t
∂ρ
+ ∇ ρ =
∂
r r
... que es la ecuación de continuidad para un fluido puro.
Si el fluido es incompresible: constante · 0vρ = ⇒ ∇ =
r r
Para la densidad de flujo molar (desarrollo análogo): ·A
A A
c
N R
t
∂
+ ∇ =
∂
rr
Sumando las ecuaciones para los dos componentes:
*
A B
A B
c c c
N N N cv
+ = 
⇒
+ = = 
r r r r ( )*
· A B
c
cv R R
t
∂
+ ∇ = +
∂
r r
Para concentración global constante: constante *
· A BR R
c v
c
+
= ⇒ ∇ =
r r

13. FenómenosdeTransporte
Tema 6 — p. 13
Para el cálculo de perfiles de concentración hay que introducir la ley de Fick:
Simplificaciones habituales
(a) Densidad y difusividad constantes (disoluciones diluidas,T constante).
constante v 0
2
· ·
·
A
A A AB A Av v D r
t
∂ρ 
+ ρ ∇ + ∇ρ = ∇ ρ + 
∂ ⇒
ρ = ⇒ ∇ = 
r rr
r r
*
· ·
· ·
A
A AB A A
A
A AB A A
v D w r
t
c
c v cD x R
t
∂ρ
+ ∇ ρ = ∇ ρ ∇ +
∂
∂
+ ∇ = ∇ ∇ +
∂
r r rr
r r rr
2
·A
A AB A A
c
v c D c R
t
∂
⇒ + ∇ = ∇ +
∂
rr, dividiendo por la masa
molecular de A ...

14. FenómenosdeTransporte
Tema 6 — p. 14
(c) ..si además la velocidad molar media es nula y no hay reacción, (sólidos o
líquidos estacionarios, y gases con interdifusión equimolar)
"Segunda ley de Fick"2A
AB A
c
D c
t
∂
= ∇
∂
constante
* * 2
*
· ·
·
A
A A AB A A
A B
c
c v v c D c R
t
R R
c v
c
∂ 
+ ∇ + ∇ = ∇ + ∂
⇒
+ = ⇒ ∇ =

r rr r
r r
(b) Concentración total y difusividad constantes (gases a baja densidad, T y P
ctes.)
( )* 2
·A A
A AB A A A B
c c
v c D c R R R
t c
∂
⇒ + ∇ = ∇ + − +
∂
rr

15. FenómenosdeTransporte
Tema 6 — p. 15
Rectangulares: AyA Ax Az
A
Nc N N
R
t x y z
∂ ∂ ∂ ∂
+ + + = ÷
∂ ∂ ∂ ∂ 
Cilíndricas: ( )
1 1 AA Az
Ar A
Nc N
rN R
t r r r z
θ∂∂ ∂∂ 
+ + + = ÷
∂ ∂ ∂θ ∂ 
Esféricas: ( ) ( )2
2
1 1 1 AA
Ar A A
Nc
r N N sen R
t r r sen r senr
φ
θ
∂ ∂ ∂ ∂
+ + θ + = ÷
∂ ∂ θ ∂θ θ ∂φ 
Rectangulares:
2 2 2
2 2 2
A A A A A A A
x y z AB A
c c c c c c c
v v v D R
t x y z x y z
  ∂ ∂ ∂ ∂ ∂ ∂ ∂
+ + + = + + + ÷ ÷  ÷∂ ∂ ∂ ∂ ∂ ∂ ∂   
Cilíndricas: 1A A A A
r z
c c c c
v v v
t r r z
θ
∂ ∂ ∂ ∂ 
+ + + = ÷
∂ ∂ ∂θ ∂ 
2 2
2 2 2
1 1A A A
AB A
c c c
D r R
r r r r z
 ∂ ∂ ∂∂  
= + + + ÷ ÷ ÷∂ ∂ ∂θ ∂  
Esféricas:
1 1A A A A
r
c c c c
v v v
t r r r sen
θ φ
 ∂ ∂ ∂ ∂
+ + + = ÷
∂ ∂ ∂θ θ ∂φ 
2
2
2 2 2 2 2
1 1 1A A A
AB A
c c c
D r sen R
r rr r sen r sen
 ∂ ∂ ∂∂ ∂   
= + θ + + ÷ ÷  ÷ ÷∂ ∂ ∂θ ∂θθ θ ∂φ    
La ecuación de continuidad en diversos sistemas coordenados
La ecuación de continuidad de A para ρ y DAB constantes

16. FenómenosdeTransporte
Tema 6 — p. 16
Ecuación de continuidad: ( ) ( )· · 1,2,...,i
i i i
D
v j r i n
Dt
ρ
= −ρ ∇ − ∇ + =
rr rr
Sumando para todos los componentes: ( )· 0v
t
∂ρ
+ ∇ ρ =
∂
r r
Ecuación de movimiento:
Ecuación de energía:
1
·
n
i i
i
Dv
g P
Dt =
 ρ = − ∇ π + ρ π = τ + δ  ∑
r rr rr r r
( ) ( ) ( )2
1
1ˆ · · · ·
2
n
i i
i
D
U v q v n g
Dt =
 
ρ + = − ∇ − ∇ π +    
 
∑
r rr r rrr
Otras ecuaciones necesarias para describir el sistema:
• Ecuación de estado: p = p(ρ,T,xi)
• Ecuación térmica de estado: Û =Û(ρ,T,xi)
• Expresiones para las densidades de flujo: ji, π, q
• Propiedades de transporte: µ, k, DAB = f(P,T,xi)
• Cinéticas de las reacciones: ri
• Campos de fuerzas: gi
Ecuación de continuidad para sistemas de varios componentes en función de las
densidades de flujo

17. FenómenosdeTransporte
Tema 6 — p. 17
Densidades de flujo en un sistema de coordenadas estacionario
(Transporte convectivo + molecular)
i
c.d.m.: vv
Energía:
Materia: n
21ˆ ·
2
1,2,...,i i
e U v v q v
w v j i n
φ = ρ + π
 
= ρ + + + π    
 
= ρ + =
r rr r
r rr rr
rr r
Las ecuaciones de variación correspondientes ...
( ) ( )
( )
Movimiento:
Energía:
t
Continuidad:
1
2
1
·
1ˆ · ·
2
· 1,2,...,
n
i i
i
n
i i
i
i i i
v g
t
U v e n g
n r i n
t
=
=
∂
 ρ = − ∇ φ + ρ ∂
∂  
ρ + = − ∇ + 
∂  
∂
ρ = − ∇ + =
∂
∑
∑
rr rr
r r r r
r r

18. FenómenosdeTransporte
Tema 6 — p. 18
ACOPLAMIENTO
Diferencia de órdenes:
0,2
DENSIDAD DE FLUJO
FUERZA IMPLUSORA
i
q
j
τ
r
r
r
{ }
, ,i i
v
T
x P g
∇
 ∇ 
   ∇ ∇ ≠   
r r
r
r r r
Ecuación de continuidad para sistemas de varios componentes en función de las
propiedades de transporte

19. FenómenosdeTransporte
Tema 6 — p. 19
Densidades de flujo
c.d.m. (newtonianos):
( ) ( ) ( )2
3
.
t
v v v τ = −µ ∇ + ∇ + µ − κ ∇ δ ÷
 
r r rr r rr
Energía: ( ) ( ) ( ) ( )
1
n
c d x x
i i
i
q q q q k T H J q
=
= + + = − ∇ + +∑
rrr r r r r
En un sistema de coordenadas estacionario:
{ }( ) ( ) ( ) 21
2
ˆ·c d x
e q q q v U v v= + + + π + ρ +  
r r r r r rr
{ }Despreciando ( ) 21
2
, · :x
q v v vτ + ρ  
r r rr
1
n
i i
i
e k T N H
=
= − ∇ + ∑
rrr

20. FenómenosdeTransporte
Tema 6 — p. 20
Materia:
( )( ) ( ) ( )
2
( )
, ,1 1
,
2
( )
1
2
( )
1
1
s
gx P T
i i i i i
n n
jx
i j ij j ki
k T p xj k
s j kk j
n
jP
i j ij j ji
jj
n
g k
i j ij j j j ki
k
j j j j j
Gc
j M M D x x
RT x
Vc
j M M D x M P
RT M
c
j M M D x M g g
RT
= =
≠≠
=
=
= + + +
 
 ∂ 
= ∇ ÷  ÷ρ ∂  
 
  
= − ∇  ÷
 ÷ρ ρ   
 ρ
= − −
ρ ρ
∑ ∑
∑
∑
r r r r r
r r
r r
r r r
1
( )
ln
n
j
T T
iij D T
=
 
 ÷
 ÷  
= − ∇
∑
r r

21. FenómenosdeTransporte
Tema 6 — p. 21
En un sistema binario ...
2
2
,
A
A B A B AB A A
A A T P
Gc
j j M M D x x
RT x M
   ∂
= − = − ∇ − ÷  ÷ ÷ρ ∂   
r r r
( )
1
lnTB A
A B A
A
V
g g P D T
M
 ρ
− − + − ∇ − ∇ ÷
ρ ρ  
r rr r
( ) 2,
ln ,
T
A
A A TT P
ABA B
D
dG RT d a k
Dc M M
ρ
= =
2
,
ln
ln
A
A B A B AB A
A T P
ac
j j M M D x
x
   ∂
= − = − ∇ − ÷  ÷ ÷ρ ∂   
r r r
( )
1
lnA B A A A A
A B T
A
M x M x V
g g P k T
RT RT M
 ρ
− − + − ∇ − ∇ ÷
ρ ρ  
r rr r

22. FenómenosdeTransporte
Tema 6 — p. 22
Ejemplo: Transferencia simultánea de calor y materia
Ecuación de continuidad:
0AzdN
dz
=
Perfil de concentración (Ley de Fick):
1
AB A
Az
A
cD dx
N
x dz
= − ⇒
−
Densidad de flujo:
1
ln
1
AAB
Az
Ao
xcD
N
x
δ −
=  ÷
δ − 
/
11
1 1
z
AA
Ao Ao
xx
x x
δ
δ   −−
⇒ = ÷  ÷
− −   
VAPOR A
+
INERTE
SUPERFICIEFRIA
CONDENSADO
Tδ
zT
0T
Ax δ
Azx
0Ax
0z = z = δ
z

23. FenómenosdeTransporte
Tema 6 — p. 23
Ecuación de energía: 0zde
dz
=
Densidad de flujo de energía:
( ) ( )0z A Az B Bz Az pA
dT dT
e k H N H N k N C T T
dz dz
= − + + = − + −%% %
Integrando:
0
0
1 exp
1 exp
Az pA
Az pA
N C
z
kT T
T T N C
k
δ
 
−  
 −  =
−  
− δ 
  
%
%
El perfil de concentración en función de la
densidad de flujo:
1 exp
1 exp
Az
ABA Ao
A Ao Az
AB
N
z
cDx x
x x N
cD
δ
 
−  
−  =
−  
− δ 
 