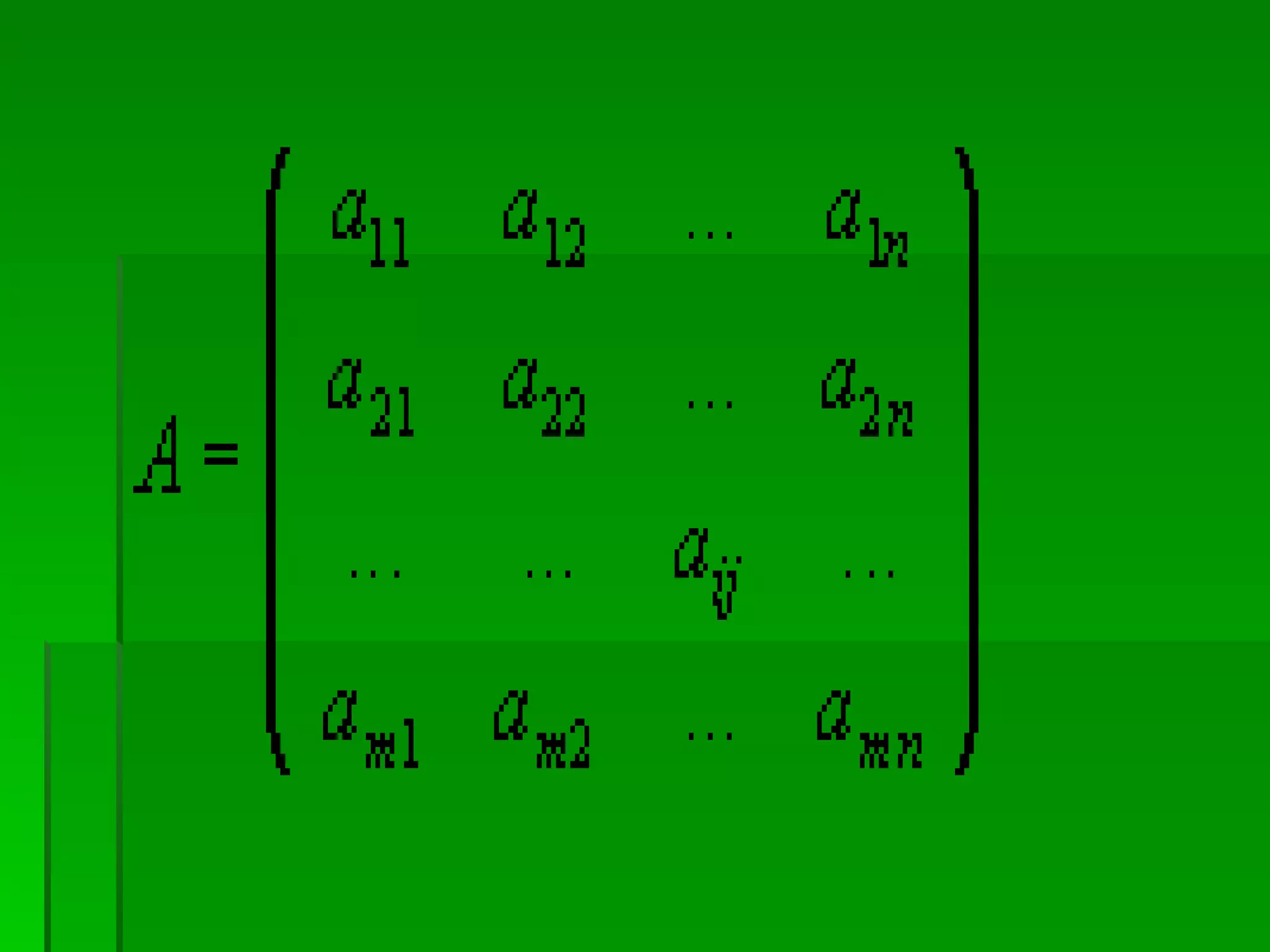
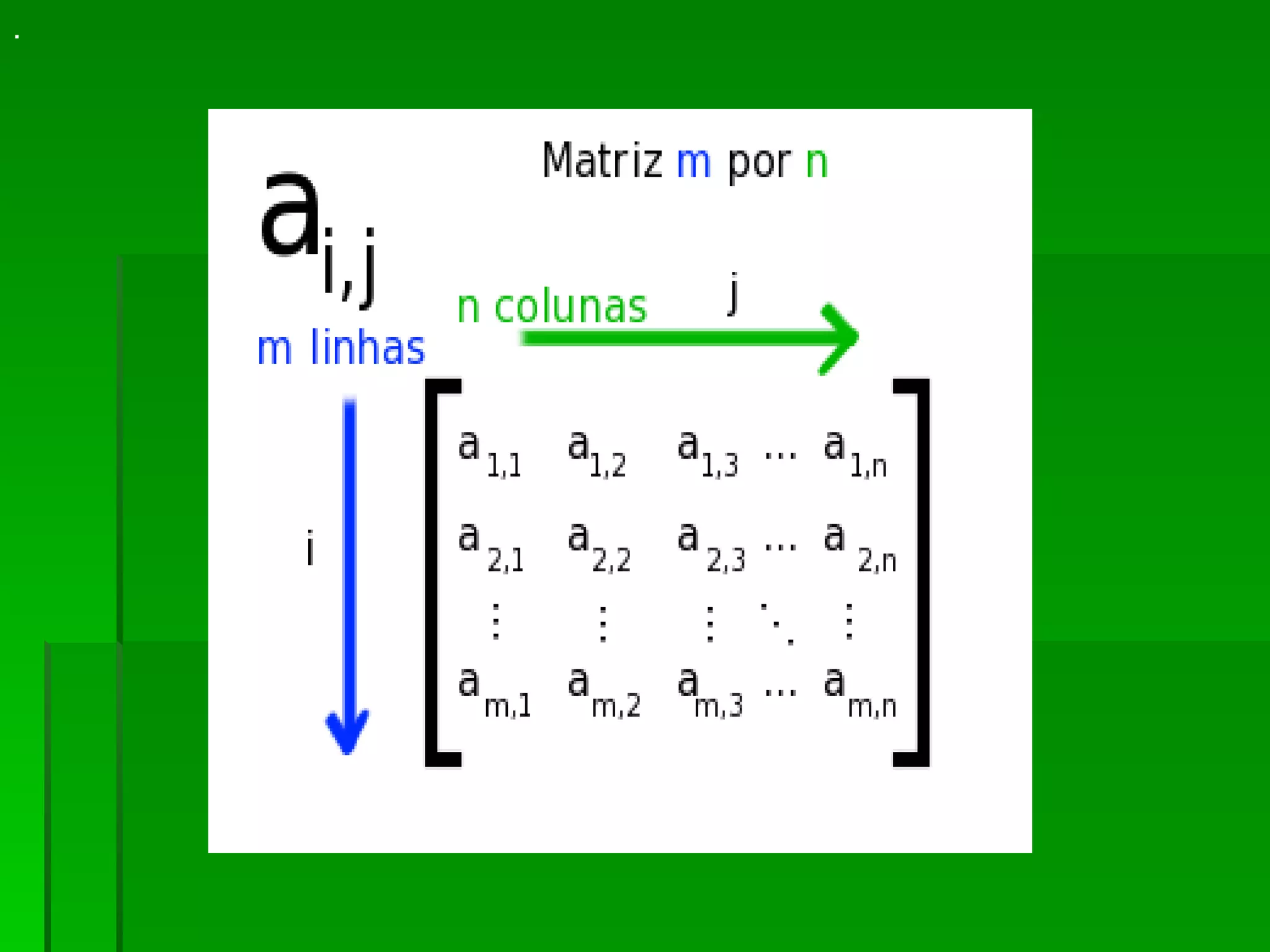
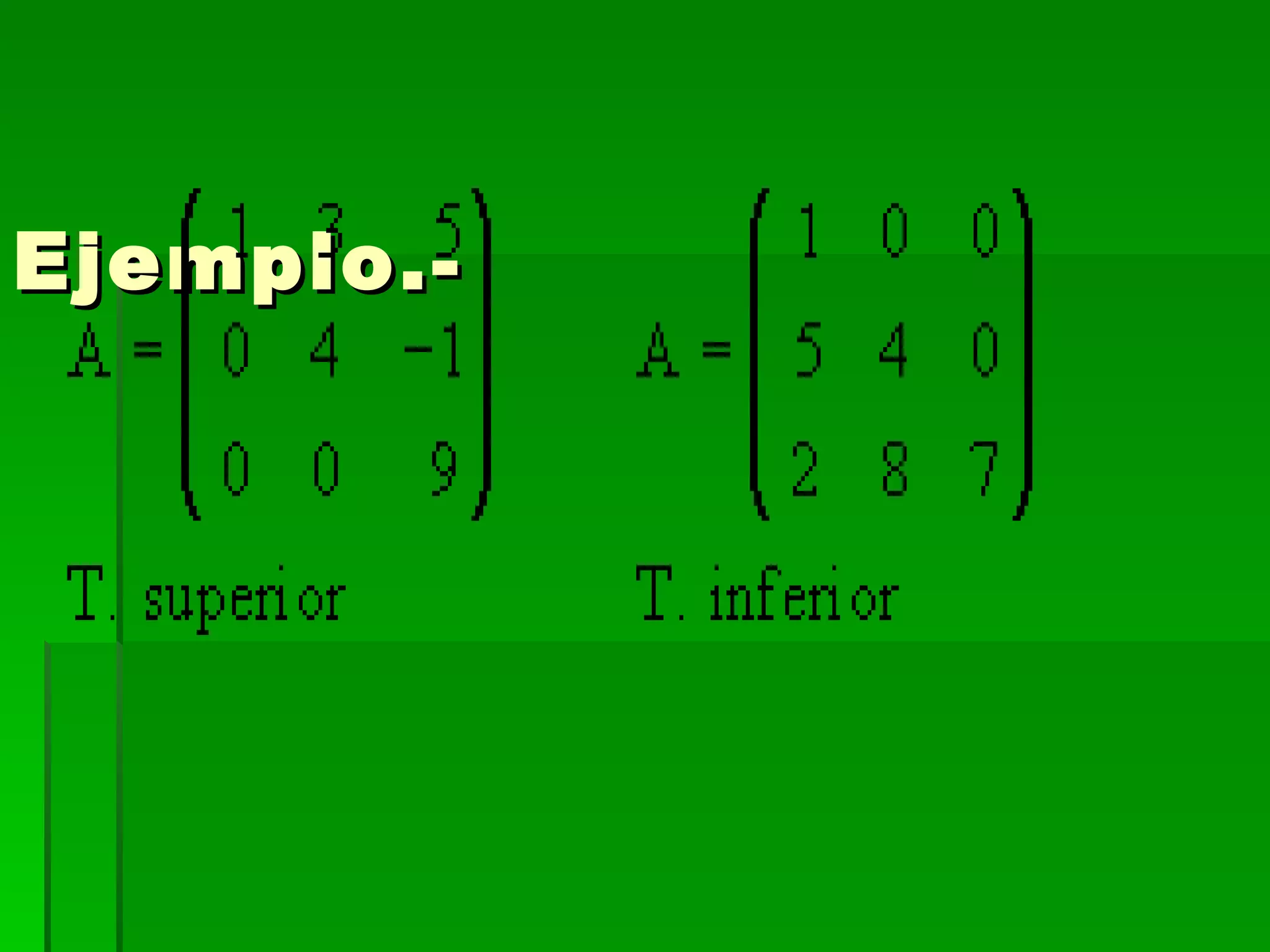
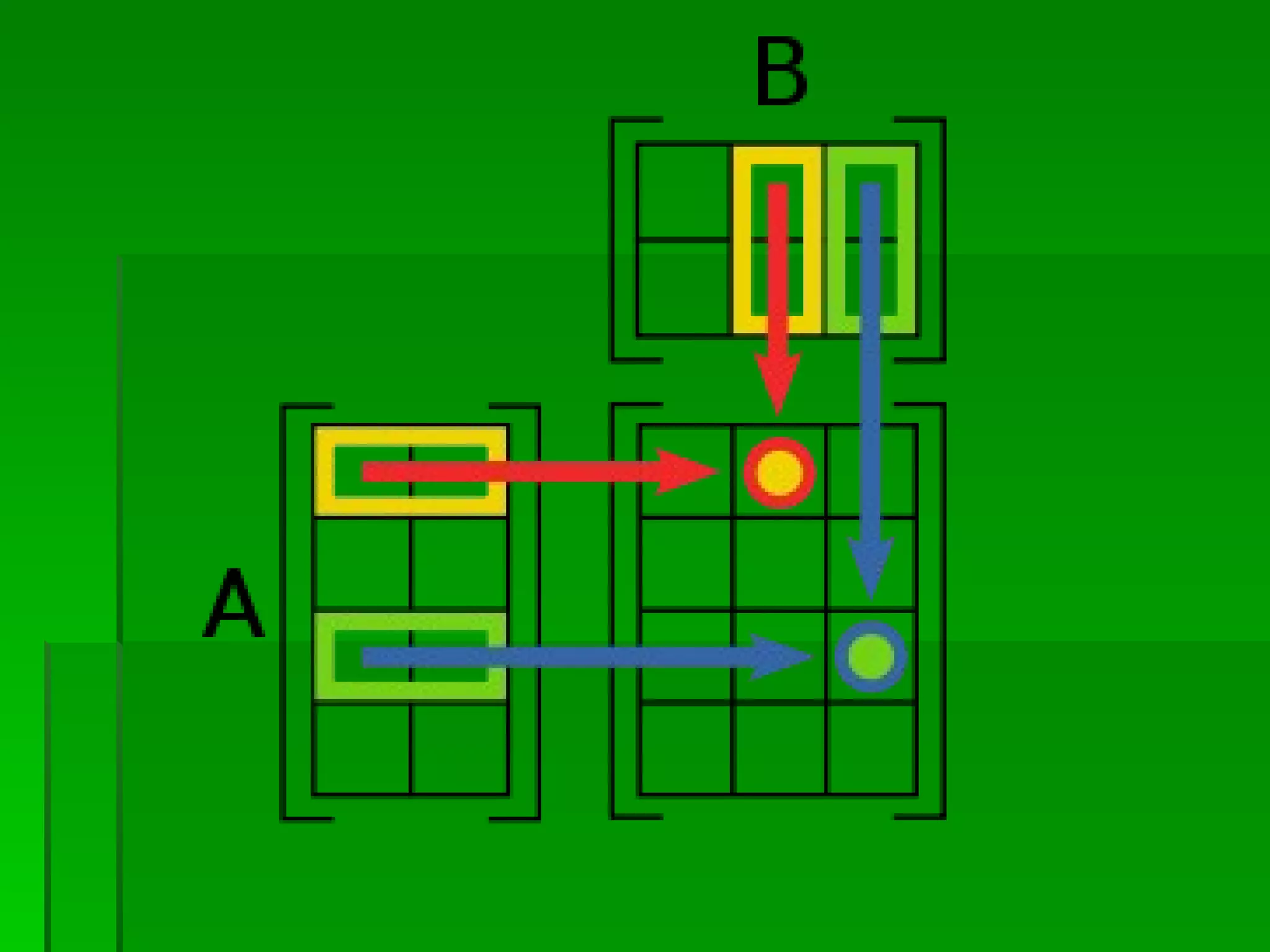
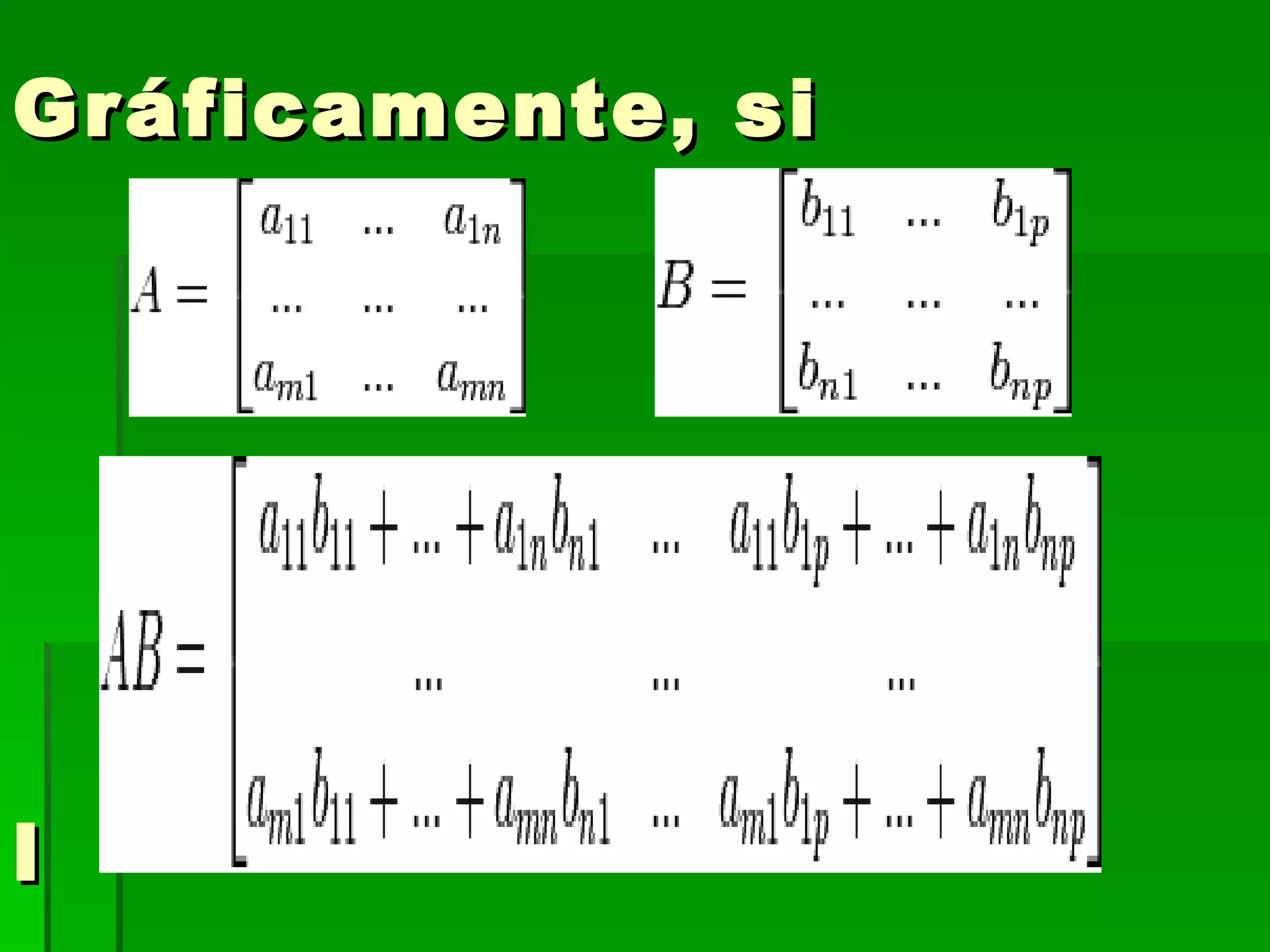
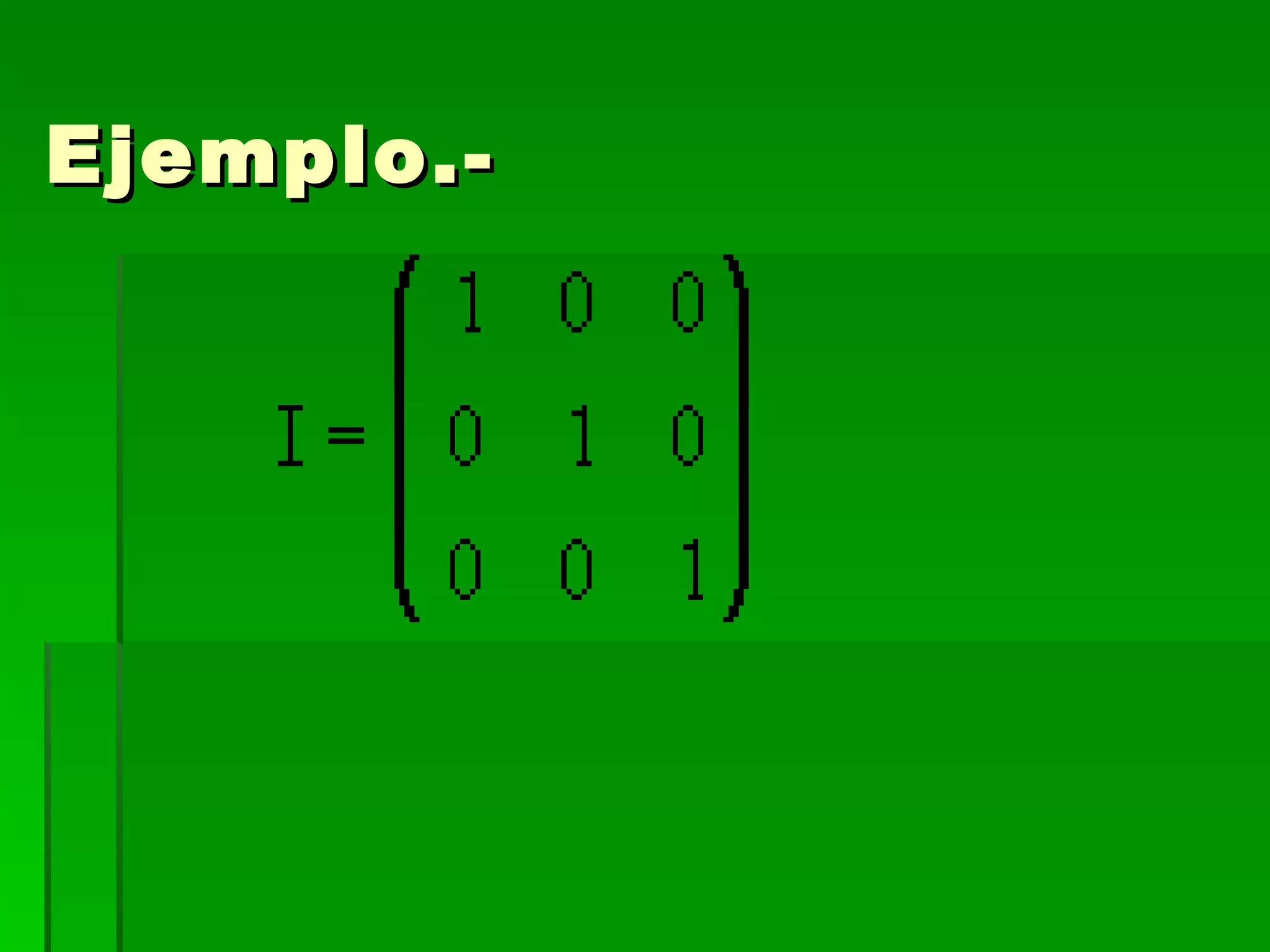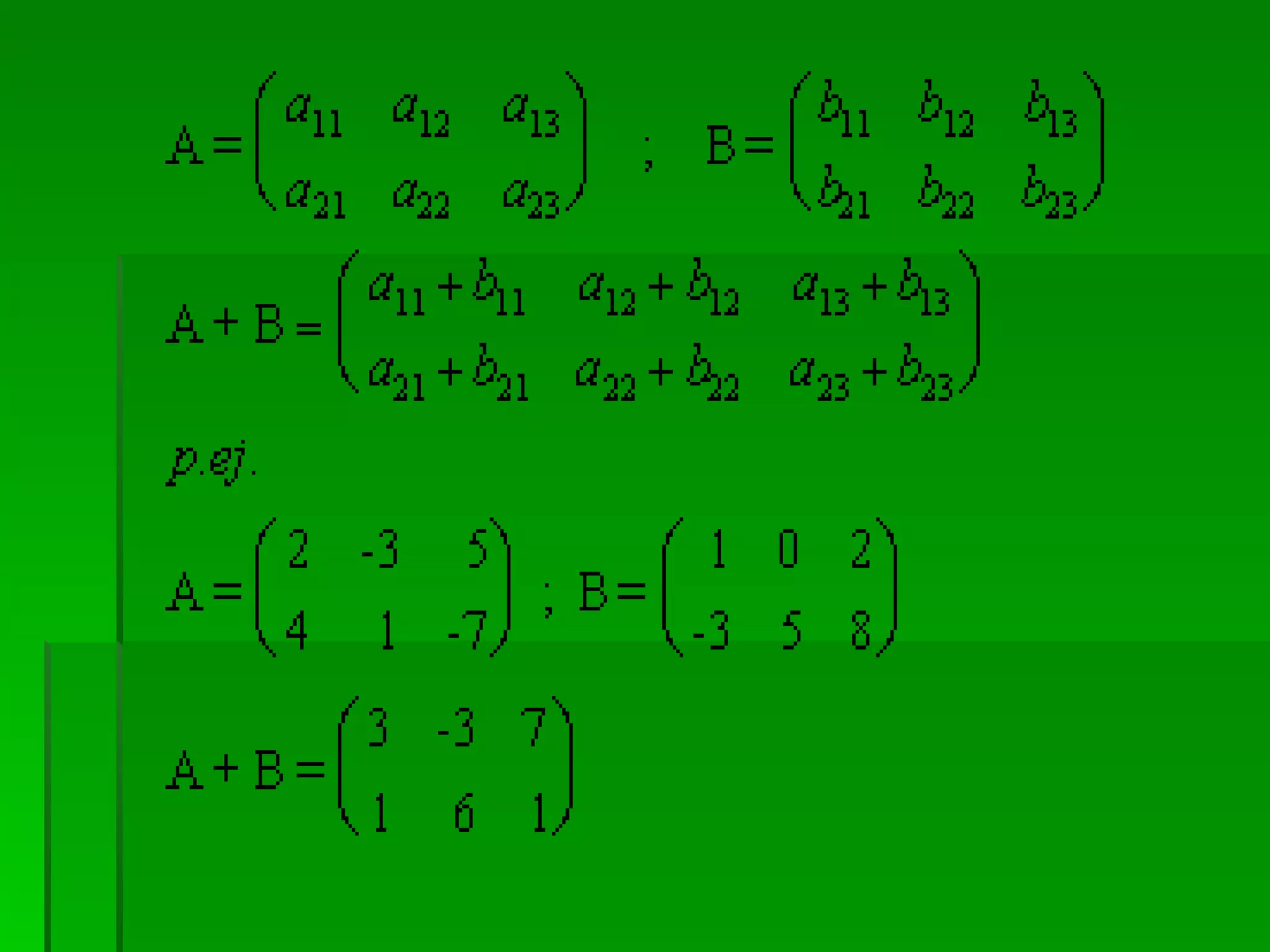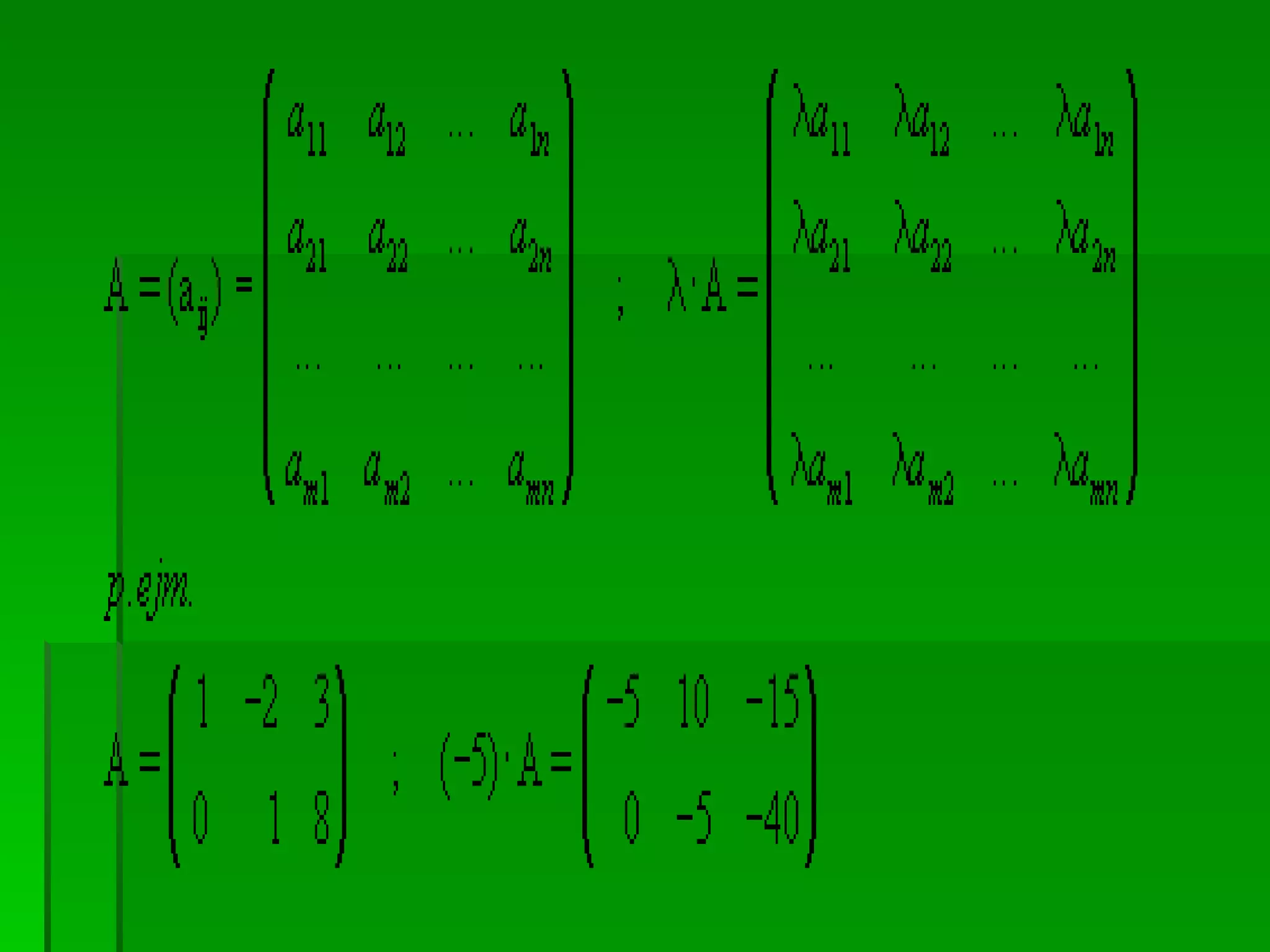El documento define una matriz como un conjunto rectangular de elementos dispuestos en filas y columnas. Describe las diferentes clases de matrices, incluyendo matrices cuadradas, simétricas, diagonales e identidad. También explica operaciones básicas con matrices como suma, multiplicación por un escalar, multiplicación de matrices y cálculo de la inversa de una matriz cuadrada.

1. MATRIZ Definición.- Se llama matriz de orden "m × n" a un conjunto rectangular de elementos a ij dispuestos en m filas en n columnas.

2. El orden de una matriz tam- bién se denomina dimensión o tamaño, siendo m y n nú- meros naturales. Las matrices se denotan con letras mayúsculas: A, B, C, ... y los elementos de las mis- mas con letras minúsculas y subíndices que indican el lugar ocupado: a, b, c, ...

3. Un elemento genérico que ocupe la fila i y la columna j se escribe a ij . Si el elemento genérico aparece entre paréntesis también representa a toda la matriz : A = ( a ij )

5. .

7. MATRICES IGUALES Dos matrices A= ( a ij ) m × n y B = ( b ij ) p × q son iguales, sí y solo si, tienen en los mismo lugares elementos iguales, es decir :

8. CLASES DE MATRICES 1)Matriz fila.- Aquella matriz que tiene una sola fila, siendo su orden 1×n. Ejemplo.-

9. 2)Matriz columna.- Aquella matriz que tiene una sola columna, siendo su orden m×1. Ejemplo:

10. 3)Matriz nula.-Si todos sus elementos son cero. También se denomina matriz cero y se denota por 0m×n. Ejemplo.-

11. 4)Matriz transpuesta.- Dada una matriz A , se llama traspuesta de A a la matriz que se obtiene cambiando ordenadamente las filas por las columnas. Se representa por A t ó A T

13. Propiedades Si A y B son matrices y A t y B t son las transpuestas, se verifica : a) (A t ) t = A b) (A + B ) t = A t + B t c) (A - B ) t = A t - B t d) (cA t ) = cA t c є R e) (A B) t = B t A t

14. 5)Matriz cuadrada.- Aquella matriz que tiene igual número de filas que de columnas, m = n, diciendose que la matriz es de orden n . Diagonal principal : son los elementos a 11 , a 22 , ..., a nn Diagonal secundaria : son los elementos a ij con i+j = n+1

15. Diagonal principal : Diagonal secundaria :

16. 6)Matriz simétrica.- Es una matriz cuadrada que es igual a su traspuesta. A = A t , a ij = a ji Ejemplo:

17. 7)Matriz antisimétrica.- Es una matriz cuadrada que es igual a la opuesta de su traspuesta. A = -A t , a ij = -a ji Necesariamente a ii = 0 Ejemplo:

18. 8)Matriz diagonal.- Es una matriz cuadrada que tiene todos sus elementos nulos excepto los de la diagonal principal. Ejemplo:

19. 9)Matriz escalar.- Es una matriz cuadrada que tiene todos sus elementos nulos excepto los de la diagonal principal que son iguales. Ejemplo.-

20. 10)Matriz identidad o unidad.- Es una matriz cuadrada que tiene todos sus elementos nulos excepto los de la diagonal principal que son iguales a 1. Tambien se denomina matriz unidad.

21. Ejemplo.-

22. 11)Matriz triangular superior.- Es una matriz cuadrada que tiene todos los elementos por debajo de la diagonal principal nulos.

23. 12) Matriz triangular inferior.- Es una matriz cuadrada que tiene todos los elementos por encima de la diagonal principal nulos.

24. Ejemplo.-

25. Algebra de matrices 1)Adición o suma de matrices.- La suma de dos matrices A = (a ij ) m × n y B = (b ij ) p × q de la misma dimen- sión (equidimensionales) : m = p y n = q es otra matriz C = A+B = (c ij ) m × n = (a ij +b ij )

27. PROPIEDADES : · Asociativa : A+(B+C) = (A+B)+C · Conmutativa : A+B = B+A · Elem. neutro : ( matriz cero 0 m×n ) , 0+A = A+0 = A · Elem. simétrico : ( matriz opuesta -A ) , A + (-A) = (-A) + A = 0

28. 2)Producto de un número real por una matriz. Para multiplicar un escalar por una matriz se multiplica el escalar por todos los elementos de la matriz, obteniéndose otra matriz del mismo orden.

30. Propiedades:

31. 3)Multiplicación de matrices. Dadas dos matrices A y B , tales que el número de co- lumnas de la matriz A es igual al número de filas de la matriz B ; es decir:

32. la multiplicación de A por B , que se denota A·B , A×B o simplemente AB , está definida como: donde cada elemento c i,j está definido por:

34. Gráficamente, si y l

35. Propiedades: a) Propiedad asociativa : (AB)C = A(BC). b) Propiedad distributiva por la derecha : (A+B)C=AC + BC. C) Propiedad distributiva por la izquierda : C(A+B)=CA+CB. d)El producto de dos matri- ces generalmente no es con- mutativo, es decir , AB≠ BA.

36. INVERSA DE UNA MATRIZ CUADRADA Se llama matriz inversa de una matriz cuadrada An y la representamos por A -1 , a la matriz que verifica la siguiente propiedad : A -1 ·A = A·A -1 = I

37. Decimos que una matriz cuadrada es "regular" si su determinante es distinto de cero, y es "singular" si su determinante es igual a cero .Es decir:

38. Propiedades:

39. MÉTODOS PARA HALLAR LA MATRIZ INVERSA : a)Aplicando la definición b)Por el método de Gauss c)Por determinantes

40. Método por determinantes. Ejemplo.- Hallar la inversa de la matriz primero calculamos el determimante :

41. Ahora calculamos cada uno de los adjuntos:

42. METODO DE GAUSS-JORDAN PARA EL CÁLCULO DE LA INVERSA DE UNA MATRIZ. Este método consiste en ir efectuando transformacio- nes ELEMENTALES P 1 ,P 2 ,..., P r entre las FILAS de la ma- triz inicial A para conseguir transformarla en la matriz identidad.

43. Las TRANSFORMACIONES ELEMENTALES que se podrán realizar con las FILAS de la matriz A serán: a) intercambiar filas. b) multiplicar una fila por un escalar. c) sumar a una fila una combinación lineal de las restantes.

44. La idea consiste en ir aplicando a la matriz A una serie de transformaciones encaminadas a conseguir obtener la matriz identidad, es decir: