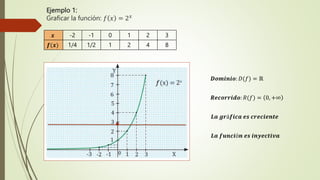
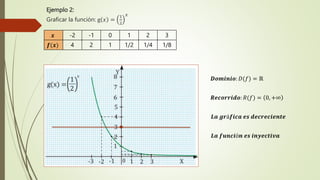
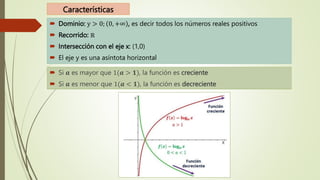
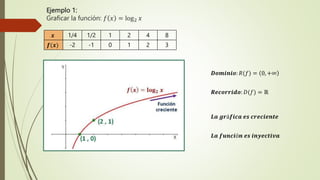
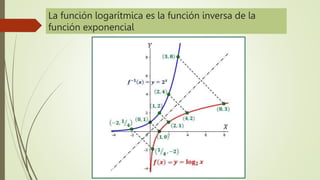
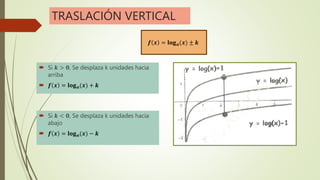
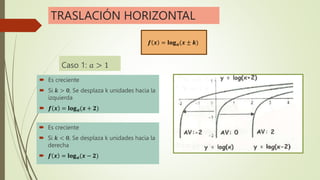
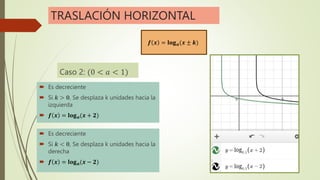
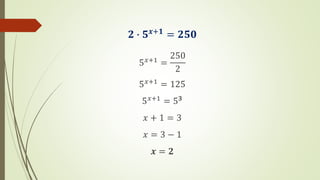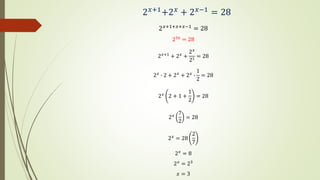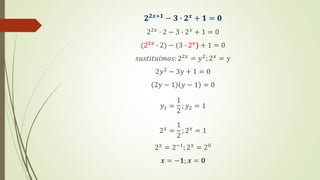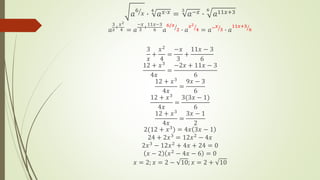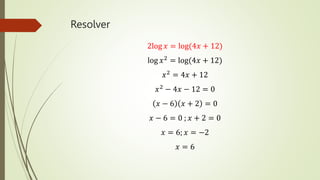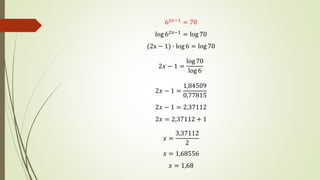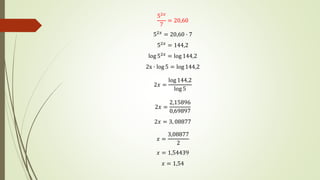El documento explica las funciones exponenciales y logarítmicas. Define las funciones exponenciales como aquellas donde la variable independiente aparece en el exponente y tiene una constante como base. Explica que las funciones exponenciales son crecientes si la base es mayor que 1 y decrecientes si la base es menor que 1. También define las funciones logarítmicas y explica que son la función inversa de las funciones exponenciales. Por último, muestra ejemplos de ecuaciones exponenciales y cómo resolverlas.

1. FUNCIONES
EXPONENCIALES

2. 𝒂𝒏 = 𝒂 ∙ 𝒂 ∙… ∙ 𝒂
Dados dos números reales a ∈ ℝ y n ∈ ℕ, definimos a la
potencia enésima de a como:
EXPONENTES
𝒏 𝑓𝑎𝑐𝑡𝑜𝑟𝑒𝑠
𝑺𝒊 𝒂 ≠ 𝟎 𝒂−𝒏 =
𝟏
𝒂𝒏
Podemos representar una raíz mediante exponentes
fraccionarios.
𝒂
𝟏
𝒏 = 𝒏
𝒂; 𝒏 ∈ ℕ, 𝒏 ≠ 𝟏, 𝒂 > 𝟎

3. FUNCIONES EXPONENCIALES
Una función exponencial es aquella en que la variable
independiente x aparece en el exponente y tiene de base una
constante a. Su expresión es:
𝒇 𝒙 = 𝒂𝒙
Siendo 𝒂 un real positivo, 𝒂 > 𝟎, y diferente de 1, 𝒂 ≠ 𝟏

4. Características
 Dominio: ℝ
Son todos los números reales
 Recorrido: y > 0; 0, +∞
Son todos los números reales positivos
 Si 𝒂 es mayor que 1(𝒂 > 𝟏), la función es creciente
 Si 𝒂 es menor que 1(𝒂 < 𝟏), la función es decreciente
La función exponencial es inyectiva

5. Ejemplo 1:
Graficar la función: 𝑓 𝑥 = 2𝑥
𝒙 -2 -1 0 1 2 3
𝒇(𝒙) 1/4 1/2 1 2 4 8
𝑫𝒐𝒎𝒊𝒏𝒊𝒐: 𝐷(𝑓) = ℝ
𝑹𝒆𝒄𝒐𝒓𝒓𝒊𝒅𝒐: 𝑅(𝑓) = 0, +∞
𝑳𝒂 𝒈𝒓á𝒇𝒊𝒄𝒂 𝒆𝒔 𝒄𝒓𝒆𝒄𝒊𝒆𝒏𝒕𝒆
𝑳𝒂 𝒇𝒖𝒏𝒄𝒊ó𝒏 𝒆𝒔 𝒊𝒏𝒚𝒆𝒄𝒕𝒊𝒗𝒂

6. Ejemplo 2:
Graficar la función: g 𝑥 =
1
2
𝑥
𝒙 -2 -1 0 1 2 3
𝒇(𝒙) 4 2 1 1/2 1/4 1/8
𝑫𝒐𝒎𝒊𝒏𝒊𝒐: 𝐷(𝑓) = ℝ
𝑹𝒆𝒄𝒐𝒓𝒓𝒊𝒅𝒐: 𝑅(𝑓) = 0, +∞
𝑳𝒂 𝒈𝒓á𝒇𝒊𝒄𝒂 𝒆𝒔 𝒅𝒆𝒄𝒓𝒆𝒄𝒊𝒆𝒏𝒕𝒆
𝑳𝒂 𝒇𝒖𝒏𝒄𝒊ó𝒏 𝒆𝒔 𝒊𝒏𝒚𝒆𝒄𝒕𝒊𝒗𝒂

7. TRASLACIÓN VERTICAL
Caso 1: 𝑎 > 1
 Si 𝒌 > 𝟎, la función es creciente
 Se desplaza k unidades hacia arriba
 Asíntota horizontal 𝒚 = 𝒌
 Dominio: ℝ
 Recorrido: 𝑘, +∞
 Si 𝒌 < 𝟎, la función es creciente
 Se desplaza k unidades hacia abajo
 Asíntota horizontal 𝒚 = −𝒌
 Dominio: ℝ
 Recorrido: −𝑘, +∞
𝒇 𝒙 = 𝒂𝒙
± 𝒌

8. TRASLACIÓN VERTICAL
Caso 2: (0 < 𝑎 < 1)
 Si 𝒌 > 𝟎, la función es decreciente
 Se desplaza k unidades hacia arriba
 Asíntota horizontal 𝒚 = 𝒌
 Dominio: ℝ
 Recorrido: 𝑘, +∞
 Si 𝒌 < 𝟎, la función es decreciente
 Se desplaza k unidades hacia abajo
 Asíntota horizontal 𝒚 = −𝒌
 Dominio: ℝ
 Recorrido: −𝑘, +∞
𝒇 𝒙 = 𝒂𝒙
± 𝒌

9. FUNCIONES
LOGARÍTMICAS

10. LOGARÍTMOS
 Sean dos números reales 𝐚 e 𝐲, siendo 𝒂 ≠ 𝟏. Se llama logaritmo de un número ℝ +
en base 𝐚 de 𝐲 al elemento al que hay que elevar el número 𝐚 para que dé como
resultado el número 𝐲.
𝒂𝒙 = 𝒚
𝒙 = 𝐥𝐨𝐠𝒂 𝒚
 Donde cualquier número positivo diferente de 1 se puede elegir como base

11. FUNCIÓN LOGARÍTMICA
 Una función logarítmica está formada por un logaritmo de base a, y es
de la forma:
𝒇 𝒙 = 𝐥𝐨𝐠𝒂(𝒙)
Siendo 𝒂 un real positivo,
𝒂 > 𝟎, y diferente de 1, 𝒂 ≠ 𝟏

12. Características
 Dominio: y > 0; 0, +∞ , es decir todos los números reales positivos
 Recorrido: ℝ
 Intersección con el eje x: (1,0)
 El eje y es una asíntota horizontal
 Si 𝒂 es mayor que 1(𝒂 > 𝟏), la función es creciente
 Si 𝒂 es menor que 1(𝒂 < 𝟏), la función es decreciente

13. Ejemplo 1:
Graficar la función: 𝑓 𝑥 = log2 𝑥
𝒙 1/4 1/2 1 2 4 8
𝒇(𝒙) -2 -1 0 1 2 3
𝑹𝒆𝒄𝒐𝒓𝒓𝒊𝒅𝒐: 𝐷(𝑓) = ℝ
𝑫𝒐𝒎𝒊𝒏𝒊𝒐: 𝑅(𝑓) = 0, +∞
𝑳𝒂 𝒈𝒓á𝒇𝒊𝒄𝒂 𝒆𝒔 𝒄𝒓𝒆𝒄𝒊𝒆𝒏𝒕𝒆
𝑳𝒂 𝒇𝒖𝒏𝒄𝒊ó𝒏 𝒆𝒔 𝒊𝒏𝒚𝒆𝒄𝒕𝒊𝒗𝒂

14. La función logarítmica es la función inversa de la
función exponencial

15. TRASLACIÓN VERTICAL
 Si 𝒌 > 𝟎, Se desplaza k unidades hacia
arriba
 𝒇 𝒙 = 𝐥𝐨𝐠𝒂(𝒙) + 𝒌
 Si 𝒌 < 𝟎, Se desplaza k unidades hacia
abajo
 𝒇 𝒙 = 𝐥𝐨𝐠𝒂(𝒙) − 𝒌
𝒇 𝒙 = 𝐥𝐨𝐠𝒂(𝒙) ± 𝒌

16. TRASLACIÓN HORIZONTAL
 Es creciente
 Si 𝒌 > 𝟎, Se desplaza k unidades hacia la
izquierda
 𝒇 𝒙 = 𝐥𝐨𝐠𝒂(𝒙 + 𝟐)
 Es creciente
 Si 𝒌 < 𝟎, Se desplaza k unidades hacia la
derecha
 𝒇 𝒙 = 𝐥𝐨𝐠𝒂(𝒙 − 𝟐)
𝒇 𝒙 = 𝐥𝐨𝐠𝒂(𝒙 ± 𝒌)
Caso 1: 𝑎 > 1

17. TRASLACIÓN HORIZONTAL
 Es decreciente
 Si 𝒌 > 𝟎, Se desplaza k unidades hacia la
izquierda
 𝒇 𝒙 = 𝐥𝐨𝐠𝒂(𝒙 + 𝟐)
 Es decreciente
 Si 𝒌 < 𝟎, Se desplaza k unidades hacia la
derecha
 𝒇 𝒙 = 𝐥𝐨𝐠𝒂(𝒙 − 𝟐)
𝒇 𝒙 = 𝐥𝐨𝐠𝒂(𝒙 ± 𝒌)
Caso 2: (0 < 𝑎 < 1)

18. ECUACIONES EXPONENCIALES
 Son de la forma
 Donde: 𝑃 𝑥 𝑦 𝑄 𝑥 son expresiones algebraicas en 𝑥
 1. Reducción a una base común: Si las dos potencias tienen la misma base entonces sus
exponentes son iguales (unicidad de potencias)
𝒂𝑷 𝒙 = 𝒂𝑸 𝒙 ; 𝒂 ∈ ℝ +
− 𝟏
Se llama ecuación exponencial a la igualdad en la que la variable se encuentra como
exponente de cualquiera de las potencias, con base constante 𝑎, 𝑎 ∈ ℝ +
− 1
RESOLUCIÓN DE ECUACIONES EXPONENCIALES
𝒂𝑷 𝒙 = 𝒂𝑸 𝒙 ↔ 𝑷 𝒙 = 𝑸(𝒙) 𝒂𝒙 = 𝒂𝒚 ↔ 𝒙 = 𝒚

19. Propiedades de los exponentes
 El producto de potencias de igual base es igual a la misma base elevada a la
suma de los exponentes.
𝒂𝒎
∙ 𝒂𝒏
= 𝒂𝒎+𝒏
, 𝒂 ∈ ℝ
 La potencia de otra potencia es igual a la base elevada a todos los exponentes
multiplicados.
𝒂𝒎 𝒏 = 𝒂𝒎∙𝒏, 𝒂, 𝒏, 𝒎 ∈ ℝ
 Cualquier número diferente a cero elevado al exponente 0 es igual a 1.
𝒂𝟎
= 𝟏, 𝒂 ∈ ℝ, 𝒂 ≠ 𝟎
 0 elevado a cualquier potencia, menos 0, es igual a 0.
𝟎𝟎 = 𝟎, 𝒂 ∈ ℝ, 𝒂 ≠ 𝟎

20. Ecuaciones Exponenciales directas
𝟐𝒙+𝟏
= 𝟐𝟓𝟔
2𝑥+1 = 28
𝑥 + 1 = 8
𝑥 = 8 − 1
𝒙 = 𝟕
𝒂𝒙
= 𝒂𝒚
↔ 𝒙 = 𝒚
𝟒𝒙+𝟏 − 𝟖 = 𝟎
4𝑥+1 = 8
4𝑥+1 = 23
(22)𝑥+1 = 23
22𝑥+2 = 23
22𝑥+2
= 𝟐3
2𝑥 + 2 = 3
2𝑥 = 3 − 2
2𝑥 = 1
𝒙 =
𝟏
𝟐

21. 𝟐𝒙−𝟏
𝟑𝒙−𝟑 = 𝟐𝟕
3
𝑥−3
2𝑥−1 = 3
3
2
𝑥 − 3
2𝑥 − 1
=
3
2
2 𝑥 − 3 = 3(2𝑥 − 1)
2𝑥 − 6 = 6𝑥 − 3
2𝑥 − 6𝑥 = 6 − 3
−4𝑥 = 3
4𝑥 = −3
𝒙 = −
𝟑
𝟒
𝒂
𝒎
𝒏 =
𝒏
𝒂𝒎; 𝒏 ∈ ℕ, 𝒏
≠ 𝟏, 𝒂 > 𝟎

22. 𝟗 ∙ 𝟑𝒙+𝟏
= 𝟐𝟒𝟑
32
∙ 3𝑥+1
= 243
32+(𝑥+1)
= 35
33+𝑥 = 35
3 + 𝑥 = 5
𝑥 = 5 − 3
𝒙 = 𝟐
𝒂𝒎 ∙ 𝒂𝒏= 𝒂𝒎+𝒏, 𝒂 ∈ ℝ

23. 𝟐 ∙ 𝟓𝒙+𝟏
= 𝟐𝟓𝟎
5𝑥+1 =
250
2
5𝑥+1
= 125
5𝑥+1 = 53
𝑥 + 1 = 3
𝑥 = 3 − 1
𝒙 = 𝟐

24. 2𝑥+1+2𝑥 + 2𝑥−1 = 28
2𝑥+1+𝑥+𝑥−1 = 28
23𝑥
= 28
2𝑥+1
+ 2𝑥
+
2𝑥
21 = 28
2𝑥
∙ 2 + 2𝑥
+ 2𝑥
∙
1
2
= 28
2𝑥
2 + 1 +
1
2
= 28
2𝑥
7
2
= 28
2𝑥
= 28
2
7
2𝑥
= 8
2𝑥
= 23
𝑥 = 3

25. 𝟐𝟐𝒙+𝟏
− 𝟑 ∙ 𝟐𝒙
+ 𝟏 = 𝟎
22𝑥
∙ 2 − 3 ∙ 2𝑥
+ 1 = 0
(22𝑥
∙ 2) − (3 ∙ 2𝑥
) + 1 = 0
𝑠𝑢𝑠𝑡𝑖𝑡𝑢𝑖𝑚𝑜𝑠: 22𝑥 = 𝑦2; 2𝑥 = 𝑦
2𝑦2
− 3𝑦 + 1 = 0
2𝑦 − 1 𝑦 − 1 = 0
𝑦1 =
1
2
; 𝑦2 = 1
2𝑥 =
1
2
; 2𝑥 = 1
2𝑥 = 2−1; 2𝑥 = 20
𝒙 = −𝟏; 𝒙 = 𝟎

26. 𝑎
6
𝑥 ∙
4
𝑎𝑥∙𝑥 =
3
𝑎−𝑥 ∙
6
𝑎11𝑥+3
𝑎
3
𝑥+
𝑥2
4 = 𝑎
−𝑥
3 +
11𝑥−3
6 𝑎
6/𝑥
2 ∙ 𝑎
𝑥2
4 = 𝑎−𝑥
3 ∙ 𝑎
11𝑥+3
6
3
𝑥
+
𝑥2
4
=
−𝑥
3
+
11𝑥 − 3
6
12 + 𝑥3
4𝑥
=
−2𝑥 + 11𝑥 − 3
6
12 + 𝑥3
4𝑥
=
9𝑥 − 3
6
12 + 𝑥3
4𝑥
=
3(3𝑥 − 1)
6
12 + 𝑥3
4𝑥
=
3𝑥 − 1
2
2(12 + 𝑥3) = 4𝑥 3𝑥 − 1
24 + 2𝑥3 = 12𝑥2 − 4𝑥
2𝑥3 − 12𝑥2 + 4𝑥 + 24 = 0
𝑥 − 2 𝑥2 − 4𝑥 − 6 = 0
𝑥 = 2; 𝑥 = 2 − 10; 𝑥 = 2 + 10

27. ECUACIONES
LOGARÍTMICAS

28. DEFINICIÓN DE LOGARITMO
FORMA EXPONENCIAL FORMA LOGARÍTMICA
𝑎𝑥 = 𝑏 log𝑎 𝑏 = 0
42
= 16 log4 16 = 2
53 = 125 log5 125 = 3
93
= 729 log9 729 = 3
Se llama logaritmo de un número ´´b´´ en una base dada ´´a´´ al exponente ´´x´´ de
la potencia a la que se debe elevarse la base para obtener el número ´´b´´
𝒂𝒙
= 𝒃 ↔ log𝒂 𝒃 = 𝒙
log𝟏𝟎 𝒂 = log 𝒂

29. 1. Hallar los logaritmos
x = log3 81
3𝑥 = 81
3𝑥 = 33
𝑥 = 3
x = log2 128
2𝑥 = 128
2𝑥 = 27
𝑥 = 7

30. 1. Hallar los logaritmos
x = log3 243
3𝑥 = 243
3𝑥 = 243
1
2
3𝑥
= (35
)
1
2
3𝑥 = 3
5
2
𝑥 =
5
2
𝑥 = log 0,01
10𝑥 = 0,01
10𝑥
=
1
100
10𝑥
=
1
102
10𝑥 = 10−2
𝑥 = −2

31. loga x =
logb x
logb a
; (a, b, c) > 0, b ≠ 1
En algunos casos es conveniente cambiar la base de una expresión
logarítmica mediante la siguiente relación de igualdad
TEOREMA DEL CAMBIO DE BASE
Si la base a la que se quiere cambiar es 10, se tiene:
loga x =
log x
log b
; (a, b, c) > 0, b ≠ 1

32. 1. Hallar log2 4, en base 10
x = log2 4
log2 4 =
log 4
log 2
log2 4 =
0,602
0,301
log2 4 = 2
𝑥 = 2
𝑥 = log2 4
2𝑥 = 4
2𝑥
= 22
𝑥 = 2

33. TEOREMAS DE LOS LOGARÍTMOS
TEOREMA ENUNCIADO EJEMPLO
loga DE LA BASE 𝐥𝐨𝐠𝒂 𝒂 = 𝟏 log2 2 = 1
loga DE 1 𝐥𝐨𝐠𝒂 𝟏 = 𝟎 log13 1 = 0
loga DE UN PRODUCTO 𝐥𝐨𝐠𝐚(𝐌 ∙ 𝐍)=𝐥𝐨𝐠𝐚 𝐌+𝐥𝐨𝐠𝐚 𝐍 log3(2 ∙ 7)=log3 2+log3 7
loga DE UN COCIENTE
𝐥𝐨𝐠𝐚
𝐌
𝐍
=𝐥𝐨𝐠𝐚 𝐌 − 𝐥𝐨𝐠𝐚 𝐍 log3
9
11
=log3 9 − log3 11
loga DE UNA POTENCIA 𝐥𝐨𝐠𝐚 𝐌𝐤=𝐤 ∙ 𝐥𝐨𝐠𝐚 𝐌 log2 53=3 ∙ log2 5
loga DE UNA RAIZ
𝐥𝐨𝐠𝐚
𝒏
𝐌𝒔 =
𝒔
𝒏
𝐥𝐨𝐠𝐚 𝐌 log3 13 =
1
2
log3 13

34. 1. Hallar log2 4+log2 2, utilizando las propiedades
𝑥 = log2 4+log2 2
x = log2(4 ∙ 12)
x = log2(4 8)
log2(4 8) =
log 48
log 2
log2(4 8) =
1,68
0,30
log2(4 8) = 5,58
𝑥 = 5,58

35. 2. Hallar log0,5 2, utilizando las propiedades
x = log0,5 2
𝑥 =
1
2
log0,5 2
1
2
log0,5 2 =
1
2
log 2
log 5
1
2
log0,5 2 =
1
2
0,301
0,301
1
2
log0,5 2 = −
1
2
1
𝑥 = −
1
2

36. Resolución de ecuaciones logarítmicas
𝐚𝐛
= 𝐱 ↔ log𝐚 𝐱 = 𝐛
log𝐚 𝐌 = log𝐚 𝐍 ↔ 𝐌 = 𝐍
Si los logaritmos de dos números (M y N) en la misma base, son
iguales entonces los números han de ser también iguales
Definición de un logaritmo
Inyectividad de un logaritmo
log 20x = log 1000
20x = 1000

37. Resolver
2log 𝑥 = log(4𝑥 + 12)
log 𝑥2 = log(4𝑥 + 12)
𝑥2 = 4𝑥 + 12
𝑥2 − 4𝑥 − 12 = 0
𝑥 − 6 𝑥 + 2 = 0
𝑥 − 6 = 0 ; 𝑥 + 2 = 0
𝑥 = 6; 𝑥 = −2
𝑥 = 6

38. 43𝑥
= 105
log 43𝑥
= log 105
3x ∙ log 4 = log 105
3𝑥 =
log 105
log 4
3𝑥 =
2,202119
0,60206
3𝑥 = 3,35712
𝑥 =
3,35712
3
𝑥 = 1,11904
𝑥 = 1,12

39. 62𝑥−1 = 70
log 62𝑥−1 = log 70
(2x − 1) ∙ log 6 = log 70
2𝑥 − 1 =
log 70
log 6
2𝑥 − 1 =
1,84509
0,77815
2𝑥 − 1 = 2,37112
2𝑥 = 2,37112 + 1
𝑥 =
3,37112
2
𝑥 = 1,68556
𝑥 = 1,68

40. 52𝑥
7
= 20,60
52𝑥
= 20,60 ∙ 7
52𝑥 = 144,2
log 52𝑥
= log 144,2
2x ∙ log 5 = log 144,2
2𝑥 =
log 144,2
log 5
2𝑥 =
2,15896
0,69897
2𝑥 = 3, 08877
𝑥 =
3,08877
2
𝑥 = 1,54439
𝑥 = 1,54

41. 𝑥 = 3 2
log 𝑥 = log 3 2
log 𝑥 = 2 log 3
log 𝑥 = 2 ∙ 0,48
log 𝑥 = 0,69
100,69 = 𝑥
𝑥 = 4,68