fisica

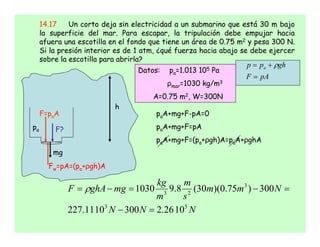
1. 14.17 Un corto deja sin electricidad a un submarino que está 30 m bajo
la superficie del mar. Para escapar, la tripulación debe empujar hacia
afuera una escotilla en el fondo que tiene un área de 0.75 m2 y pesa 300 N.
Si la presión interior es de 1 atm, ¿qué fuerza hacia abajo se debe ejercer
sobre la escotilla para abrirla?
Datos: pa=1.013 105 Pa
ρmar=1030 kg/m3
A=0.75 m2, W=300N
pAF
ghpp a
=
+= ρ
pa
mg
Fw=pA=(pa+ρgh)A
F?
h
paA+mg+F-pA=0
paA+mg+F=pA
paA+mg+F=(pa+ρgh)A=paA+ρghA
F=paA
mm
s
m
m
kg
mgghAF
53
3
23
1026.23001011.227
300)75.0)(30(8.91030
=−
=−=−= ρ

2. 14.16 Un recipiente cerrado se llena parcialmente con agua (ρagua=1000
kg/m3). En un principio, el aire arriba del agua está a presión atmosférica
(pa=1.013 105 Pa) y la presión manométrica en el recipiente es de 2500 Pa.
Después, se bombea aire adicional al interior, aumentando la presión del
aire sobre el agua en 1500 Pa. a) Calcule la nueva presión manométrica en el
fondo. b) ¿Cuánto deberá reducirse el nivel del agua en el recipiente para
que la presión manométrica en el fondo vuelva a ser de 2500 Pa? (La
presión del aire sobre el agua se mantiene a 1500 Pa sobre la presión
atmosférica).
Datos: pa=1.013 105 Pa
ρagua=1000 kg/m3
(p-p1)i=2500 Pa
ghpp a ρ=−
a) (p-p1)i=2500 Pa
p’=2500 Pa+1500 Pa=4000 Pa
hagua
p1
p
b) El cambio del nivel del agua debe compensar el cambio de presión:
1500 Pa=ρwaterg∆h=
m
smmkg
Pa
h 15.0
)/(8.9)/(1000
1500
23
==∆

3. FLOTACION & PRINCIPIO DE ARQUIMEDES
El PRINCIPIO DE ARQUIMEDES establece que:
Si un cuerpo está parcial o totalmente sumergido en un fluido,
éste ejerce una fuerza hacia arriba sobre el cuerpo igual al peso
del fluido desplazado por el cuerpo
y Consideremos una porción arbitraria de
fluido en reposo con densidad ρliq. El
fluido está en equilibrio, así que la suma
de todas las componentes de fuerza
sobre esta porción de fluido es 0.
p2A
p1A
Las fuerzas de superficie sobre las
paredes laterales son iguales y opuestas,
y se cancelan.
Las componentes verticales son las
fuerzas de superficie y el peso de la
porción de fluido

4. La fuerza B debe ser de igual magnitud que
el peso de la porción de fluido
mg = ρliqVg=ρliqA·dyg
Ahora quitamos el fluido que está dentro de la
superficie y lo reemplazamos por un cuerpo sólido cuya
forma es idéntica. La presión en cada punto es la misma
que antes, de modo que la fuerza total hacia arriba
ejercida por el fluido sobre el cuerpo es también la
misma, igual en magnitud al peso mg del fluido que se
desplazó para colocar el cuerpo.
B= ρliqVg
La presión p2 sobre la superficie inferior es
mayor que p1 por la ley de Pascal, la fuerza
resultante B está hacia arriba:
B=p2A-p1A=(pa+ ρliqgy2)A-(pa+ ρliqgy2)A=
ρliqgdy
B
mg
p2A
p1A
y
y1
y2
p1p2
Esta fuerza hacia arriba es la FUERZA DE FLOTACION que
actúa sobre el cuerpo sólido. La linea de acción pasa por el
centro de gravedad del fluido desplazado.
dy

5. FLOTACION
Fluido con
densidad ρfluido
Cuerpo con
densidad ρc y
volumen V
W= ρcVg
V
B= ρfluido Vg
El cuerpo flota si la fuerza de
flotación B es mayor que el peso
W del cuerpo:
ρfluido Vg > ρcVg
ρfluido > ρc
B= ρfluido Vg
W= ρcVg
El cuerpo no flota si la fuerza de
flotación B es menor que el peso
W del cuerpo:
ρfluido Vg < ρcVg
ρfluido < ρc

6. PREGUNTA: ¿Como pueden flotar barcos de acero en
agua? (la densidad del acero es mayor que
la densidad del agua)
RESPUESTA: Los barcos adentro estan “vacíos” (llenos
de aire, personas, cosas..) y la densidad
media es menor que la densidad del agua.

7. Arquímedes de Siracusa (Aρχιµήδης)
287-212 aC
Se cuenta que Hierón II (monarca de Siracusa) hizo entrega a un platero de la
ciudad de ciertas cantidades de oro y plata para el labrado de una corona. Finalizado
el trabajo, Hierón, desconfiado de la honradez del platero solicitó a Arquímedes que
determinara la ley de metales de la corona, conservando la corona en su integridad.
Arquímedes, preocupado por no encontrar solución al problema, al sumergirse en una
tina para bañarse se dio cuenta que el nivel del agua en la tina subía al sumergirse.
Pensando en ello llegó a la conclusión que al entrar su cuerpo en la bañera, ocupaba un
lugar que dejaba de ser ocupado por el agua y que él pesaba menos de una cantidad
igual al peso del agua desplazada. Fue tal su excitación que salió contento por las
calles de Siracusa (desnudo!!) gritando “eúreka” (εùρηκα= he encontrado)
Pesando la corona en aire y agua pudo comprobar que la densidad de la corona no
correspondía a la densidad del oro, y que el platero había estafado al monarca.

8. 14.21 Una plancha de hielo flota en un lago de agua dulce
(ρagua=1000kg/m3). ¿Qué volumen mínimo debe tener para que una mujer de
45 kg pueda pararse en ella sin mojarse los pies? (ρhielo=920kg/m3)
Datos: ρagua=1000kg/m3
ρhielo=920kg/m3
m=45kg
VgB
Vm
aguaρ
ρ
=
=
3
3
563.0
)/)(1000920(
45
)(
)(
0)(
m
mkg
kgm
V
gmVg
gmVg
VgBgmVg
aguahielo
w
waguahielo
waguahielo
aguawhielo
=
−−
=
−−
=
=−−
=+−
==+
ρρ
ρρ
ρρ
ρρ
PRINCIPIO DE ARQUIMEDES
mwg
mhielog=ρhieloVg
B

9. SOLUCIÓN
a) El volumen de la estatua es:
La fuerza de flotación es B = mwaterg=ρwaterVg:
La suma de las fuerzas es 0:
EJEMPLO 14.5
Una estatua de oro sólido (m=15 kg) está siendo levantada de un
barco hundido. ¿Qué tensión hay en el cable cuando la estatua está en
reposo y a) totalmente sumergida? b) ¿Fuera del agua? (La densidad
ρgold del oro es 19.3 103 kg/m3, la densidad del agua del mar es 1.03
103 kg/m3.
T
mg
B
34
33
107.7
)/(103.19
15
m
mkg
kgm
V
gold
−
===
ρ
s
m
m
m
kg
B 84.78.9107.71003.1 2
34
3
3
=⋅⋅= −
s
m
kgBmgT
mgTBFy
13984.78.915
0
2
=−⋅=−=
−+==Σ

10. SOLUCIÓN
Cuando la estatua está en aire la fuerza de flotación es
B = mairg=ρairVg=1.2 (kg/m3)·7.7 10-4m3·9.8 (m/s2)=
9.1 10-3 N
Entonces
T=mg-B ~ mg ~ (15 kg)(9.8 m/s2)=147 N
TB
mg

11. 14.24 Un cable anclado al fondo de un lago de agua dulce sostiene una esfera
hueca de plástico bajo la superficie. El volumen de la esfera es de 0.650 m3 y
la tensión en el cable es de 900 N. a) Calcule la fuerza de flotación ejercida
por el agua sobre la esfera. b) ¿Qué masa tiene la esfera? c) El cable se
rompe y la esfera sube a la superficie. En equilibrio, ¿qué fracción del volumen
de la esfera estará sumergida?
T
B
W=meg
Datos: ρagua=1000kg/m3
Ve=0.650 m3
T= 900 N
VgB aguaρ=
smmmkgVgBa agua 6370)/8.9)(650.0)(/1000() 233
=== ρ
kg
smg
TB
mTBgm
gmTBb
ee
e
558
/8.9
)9006370(
0)
2
=
−
=
−
=⇒−=
=−−

12. %9.85859.0
6370
)/8.9)(558('
'
'')
2
=====
=
===
smkg
B
gm
gV
gm
V
V
g
gm
V
gmWgVBc
e
agua
e
agua
e
eagua
ρ
ρ
ρ
V ‘
respuesta a)
Llamemos V ’ el volumen sumergido y B ‘ la fuerza
de flotación que actúa sobre la esfera cuando ésta
flota

13. 14.25 Un bloque cúbico de madera de 10 cm por lado flota en la interfaz
entre aceite y agua con su superficie inferior 1.5 cm bajo la interfaz
(ρaceite=790 kg/m3). a) ¿Qué presión manométrica hay en la superficie de
arriba del bloque? b) ¿Y en la cara inferior? c) ¿Qué masa y densidad tiene
el bloque?
Datos: ρagua=1000kg/m3
ρaceite=790 kg/m3
L=10 cm
h=1.5 cm, h1+h2=L
VgB
Vm
ghpp
aguaρ
ρ
ρ
=
=
+= 0
Pamsmmkgghpp aceite 3.117)015.0)(/8.9)(/790( 23
0 ===− ρ
Pamsmmkgmsmmkg
ghhhgpp aguaaceite
2.921015.0)/8.9)(/10(1.0)/8.9)(/790(
)(
23323
210
=+
=++=− ρρ
a)
b)
c)
33
2363
2433243
2121
/1082.0
)/8.9(1010
05.8
05.8
05.847.158.6
)015.0)(10100)(/10()085.0)(10100)(/790(
mkg
smm
Vgmg
mmmkgmmmkg
gAhgAhgVgVmg
maderamadera
aguaaceiteaguaoil
==⇒==
=+
=+
=+=+=
−
−−
ρρ
ρρρρ
aceite
agua
L
h
h1
h2
L
L

14. 14.19 Un tanque ahusado presurizado para un cohete contiene 0.250 cm3
de queroseno, con masa m=205 kg. La presión en la superificie
del queroseno es de p0=2.01 105 Pa. El queroseno ejerce una fuerza
de 16.4 kN sobre el fondo del tanque, cuya área es A=0.07 m2.
Calcule a) la densidad y b) la profundidad del queroseno.
p0
h?
A
p=p0+ρkgh
F=pA
Datos: p0=2.01 105 Pa
V=0.250 cm3, m=205 kg
A=0.07 m2, Fk=16.4 kN
V
m
pAF
ghpp a
=
=
+=
ρ
ρ
La densidad del queroseno se puede calcular
con m y V:
3
6
363
10820
1025.0
205
250.0
205
m
kg
m
kg
cm
kg
V
m
q ==== −
ρ
m
g
p
mhp
m
gh
mA
ghpFAghp
q
q
qq
14.407.0
104.16
07.0
104.16
07.0
104.16104.16
104.16)(
2
3
2
3
2
33
3
=
−
=⇒−=
==+⇒==+
ρ
ρ
ρρ