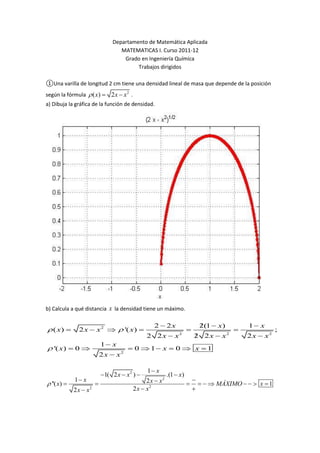
1. Departamento de Matemática Aplicada
MATEMATICAS I. Curso 2011-12
Grado en Ingeniería Química
Trabajos dirigidos
①Una varilla de longitud 2 cm tiene una densidad lineal de masa que depende de la posición
según la fórmula  ( x)  2 x  x 2 .
a) Dibuja la gráfica de la función de densidad.
b) Calcula a qué distancia x la densidad tiene un máximo.
2  2x 
2(1  x) 1 x
 ( x)  2 x  x 2   '( x)    ;
2 2x  x 2

2 2x  x 2
2 x  x2
1 x
 '( x)  0   0  1 x  0  x  1
2 x  x2
1 x
1( 2 x  x 2 )  .(1  x)
1 x 2 x  x2 
 ''( x)       MÁXIMO    x  1
2x  x 2 2 x  x2 

2. c) Calcula su masa, es decir:
2
m    ( x)dx
0
2 2 2
m( x )   2 x  x 2 dx   ( x 2  1  2 x)  1.dx   ( x 2  2 x  1)  1.dx
0 0 0
( x  1) 2  1.dx  u  x  1}
2
I 
0
2
I  1  u 2 .du
0
Aplicando las propiedades de la integración de funciones irracionales reciprocas llegamos al
siguiente resultado:
1
m  ((u 1  u 2 )  arcsen(u ))
2
Ahora realizamos un cambio de base, ya que tenemos en vez de en x , lo tenemos en u .Si
teníamos que x era 0 y 2. Como tenemos que u  x  1; obtenemos que:
u  x 1  u  2 1  u  1
u  x  1  u  0  1  u  1
Para acabar sustituimos los nuevos límites con u :
1 1
[(1 1  12  arcsen(1))]  [ 1 1  ( 12 )  arcsen( 1))] 
2 0
2
0
1  1    
( ) ( )  
2 2 2 2 4 4 2
d) Calcula su centro de gravedad, es decir:
1 2
m 0
xG  x. p( x)dx
1 2
xG  0 x 2 x  x dx
2
m
I1
 u  ( x  1) 
 u  x 1 
2 2   1
I1   x (2 x  x 2  1)  1   x ( x  1) 2  1     1 x 1  u 
2
0 0
 x  u 1 
 Lim  1y  1
 
1 1 1 1
I1   (u  1) 1  u 2   u 1  u 2  1  u 2   u2  u4   1 u2
1 1 1 1
1
  u   
2
1 1 1 1
 1 u   (u )   1 u   u        0 
2 2 2
1 1 1 1
 2  2  1 2 2
0
1  2 
 
xG  .  . 1
m 2  2
 

3. e) Calcula el momento de inercia respecto al origen de coordenadas, es decir:
2
I 0   x 2 p( x)dx
0
f) Calcula su momento de inercia respecto al centro de gravedad, es decir:
2
P(t1 , t2 )   ( x  xG )2 p( x)dx
0
I G   ( x  1) 2 p( x)   ( x  1) 2 2 x  x 2   ( x  1) 2 (2 x  x 2  1)  1 u  x  1
2 2 2
0 0 0
1
2 1 1 1 1 u2 
 1 u   u 1 u   u u   (u )   
( x  1) 2 2 2 2 2 4 2
u  
2
0 1 1 1 1 2  1
1
u2  1 1
  22 0
2  1
② La densidad de probabilidad de que un suceso ocurra en un tiempo t sigue una ley
empírica dada por p(t )  Kt 2et . La probabilidad de que el suceso ocurra en algún momento
en el intervalo (t1 , t2 ) viene dada por:
t2
P(t1 , t2 )   p( x)dx
t1
a) Sabiendo que el suceso va a ocurrir en algún momento, calcula el valor de K .
(Entonces la probabilidad P(0, ) debe valer 1).
 u  t2 du  2t.dt
P(0, )   2 t
Kt e  t t
 t 2 Ke t  2k  te t dt
0 dv  e dt v  e
I1
u t du  dt
I1   te  t dt  t
 I1  te  t  e  t
dv  e v  e  t
P(0, )   Kt 2 et  2 K (te t  e t )
t 2 2t 2 2
lim[ K ( t
 t  t )]  (2 xL ' H )  K t  1  0 K  1  K   ; K 
t  e e e e
b) Dibuja la gráfica de la densidad de probabilidad entre 0 y 100.

4. ③Para cada par de condiciones siguientes, encuentra y dibuja una función que las cumpla:
a) f '( x)  6 x 2  5 y f (1)  3
2

6 x3
f ( x)   6 x 2  5   5x

3
f ( x)  2 x3  5 x  K  3  f (1)  2 x 3  5 x  K  3
25 K  3 K  6
2 x3  5 x  6  0
Gráfica:

5. b) f '( x)  sen( x)  1 y f (1)  3
f ( x)   sen( x)  1   sen( x)dx   dx  x  cos( x)  K
x  cos( x)  K ; f (0)  1;1  cos(0)  K  1  K  1
f ( x)  x  cos( x)  1  0
x
c) f '( x)  y f (2)  1
x 1
2
x x A B
 x 2  1  ( x  1)2  x  1  ( x  1)2
A( x  1)  B Ax  A  B
 x
( x  1) 2 ( x  1) 2
 A 1   A  1
  A 1  B  A  0  B  A  B 1  
 B  A  0  B  1
1 1 1
 x  1   ( x  1)2  ln | x  1|  x  1  K
1 1
f (2)  ln | x  1|   K  1  ln |1|   K  1
x 1 1
0 1  K  1
K 2
1
f ( x)  ln | x  1|  20
x 1

6. d) f '( x)  f ( x) y f (0)  1
f ( x)  e x
f '( x)  e x  f ( x)   e x  e x
f '( x)  f ( x)
e0  1  f (0)  1

7. ④ Dada una función y  f ( x) , continua en todo , se puede descomponer en dos partes,
P( x) e I ( x) , simétricas, par e impar respectivamente, de manera que f ( x)  P( x)  I ( x) .
f ( x)  f ( x) f ( x)  f (  x)
Para ello basta tomar I  , y P( x)  . Para la función
2 2
f ( x)  cos( x  1) ,
a) Dibuja la función.

8. b) Calcula y dibuja sus partes par e impar.
IMPAR PAR
f ( x)  f (  x) f ( x)  f (  x)
I ( x)  P( x) 
2 2
cos( x  1)  cos( x  1)
I ( x) 
2
cos( x  1)  cos( x  1)
P( x) 
2
c) Calcula la integral
3
3
 f ( x)dx
f ( x)   cos( x  1)  sen( x  1)3  sen(4)  sen(2)  0, 209354
3 3

3
3 3
d) Calcula la integral
3
 2P( x)dx
0
3  cos( x  1)  cos( x  1)  3 3 3
3

2
 
2
  3 cos( x  1)  cos( x  1)  3 cos( x  1)  3 cos( x  1) 

sen( x  1)3  sen( x  1)3  0,3049
3 3
Repita los cálculos anteriores para la función g ( x)  cos( x 2  x  1)  1 . Como no se puede
obtener una expresión de la integral, haz una evaluación numérica de la misma.
g ( x)  cos( x 2  x  1)  1

9. [cos( x 2  x  1)  1]  [cos ( x) 2  x  1  1]
P( x) 
2
[cos( x 2  x  1)  1]  [cos ( x) 2  x  1  1]
I ( x) 
2
Evaluación Numérica
-5 0,8705
-4 0,1057
-3 0,1204
-2 0,8394
-1 1,5403
0 1,5403
1 0,8394
2 0,1204
3 0,1057
4 0,8705
5 1,7548
1
⑤ Dada la función y  ,
x 1
2
a) Calcula sus puntos críticos.
0
0( x 2  1)  2 x(1)
y '( x)   0  2 x  0  x  0  Pto.Crítico
( x 2  1) 2
2 x 2( x 2  1) 2  4 x( x 2  1)2 x 
y '( x)   y ''( x)      MÁXIMO. x  0
( x 2  1) 2 ( x 2  1) 4 
b) ¿En qué puntos tiene la recta tangente a la curva su pendiente máxima?
Recta tangente a la curva  y '( x)  z ( x)
2 x
z ( x) 
( x 2  1) 2
2 x 2( x 2  1) 2  8 x 2 ( x 2  1)
z ( x)  2  z '( x)   0  MAX  MIN
( x  1) 2 ( x 2  1) 4
 8 x 2 ( x 2  1)  2( x 4  2 x 2  1)
8x4  8x2  2 x4  4 x2  2
 1
 x1  
6x  4x  2  
4 2
3
 x  1 
 2
c) Dibuja la gráfica y las rectas tangentes en dichos puntos.

10. Calcula en que puntos es máxima pendiente de la tangente a la función y  sen( x) .
y  sen( x)
y '( x)  cos( x)  P( x)  Pendiente
P '( x)  cos( x)
cos( x)  0

x  arcsen(0)   Pto.Maximo
2
⑥ La cantidad de luz que llega a una superficie es proporcional a la intensidad de la fuente
luminosa, inversamente proporcional al cuadrado de la distancia de la distancia desde dicha
fuente a la superficie, y proporcional al seno de ángulo de incidencia de la luz (ángulo que
forma el rayo con la horizontal. Se tiene una estancia cilíndrica de radio 5 m y altura otros 5 m.
Determina a que distancia se ha de colocar el foco de luz para que las esquinas reciban la
máxima iluminación.
⑦El cometa Halley sigue una trayectoria alrededor del Sol dada por la ecuación en
coordenadas polares
0,5716
r ( )  .
1  0,968cos( )
a) Dibuja la gráfica en coordenadas polares de la trayectoria.

11. b) Calcula el máximo y el mínimo del radio.
0,5716 0(1  0,968cos( ))  0,968sin( )
r ( )   r '( )  0
1  0,968cos( ) (1  0,968cos( ))
0,968sin( )
r '( )    0  sin( )  0    sin 1 0    0
(1  0,968cos( )) 2
0,968sin( )
r ''( )  
(1  0,968cos( ))2
(0,968cos( )  (1  0,968cos( ))  (0,968sin( )  (0,968sin( ) 
r ''( )    Maximo
(1  0,968cos( ))4 
r ( )  0, 29
dx
c) Sabiendo que x  r cos( ) , calcula
d
x
x  r cos( )  r 
cos( )
x 0,5716 0,5716 cos( ) dx 0,5716sin( ) dx
 x     0,5904
cos( ) 1  0,968cos( ) 1  0,968cos( ) d 0,968sin( ) d
⑧ La ecuación de estado de Van der Waals viene dada por:
nRT an2
p 
V b V 2
Calcula los valores de los parámetros a y b de la ecuación anterior sabiendo que la tangente a
la isoterma en el puntico ( pc , Tc ,Vc ) debe ser horizontal y además un punto de inflexión.
Aplicando lo anterior dibuja la isoterma correspondiente a la temperatura crítica de un mol de
agua cuyos parámetros son ( pc  218,3 atm, Vc  0, 056 l y Tc  647, 4 ºK ) .
nRT an 2
p 
V b V 2
dp RT 2a
  3  0  Horizontal
dV T (V  b) V
2
d2y 2 RT 6a
  3  0  Pto.Inflexión
d x T (V  b) V
2 3
 
RT 2a 
  3 0
(V  b ) 2
V 1 2 6
 4
     6V  6b  4V  2V  6b  V  3b
2 RT 6a 2 6 V V  b
 0 ( ) ( )
(V  b) 3 V 4 (V  b) V 
 RT 2a RT 2a 8a
 3 0   27b 3 RT  8 b 2 a  T 
(V  b) V
2
(2b) 2
27b 3
27bR

12. Ra8 8Ra
RT a a 8 Ra a
p  2  27bR  p  27bR  2  p   2
(V  b) V 3b  b 2b V 2
54b R 9b
1 a a
 p 2
 p
27 b 27b 2
Segunda Parte:
0, 056
Vc  0, 056  3b  0, 056  b   0,1866
3
a
Pc  218,3   218,3  a  (218,3).(27.(0,1866))  1099,83  a  1099,83
27b2
⑨ La ecuación de la recta que mejor aproxima a una función y  f ( x) en el punto x  0 se
puede obtener tomando una recta genérica r ( x)  mx  n y exigiendo que ambas funciones y
sus derivadas sean iguales en dicho punto. De ésta manera se obtiene: r  f '(0)  r (0)  n y
f '(0)  r '(0)  m , siendo por tanto la recta que buscamos r  f '(0) x  f (0) , es decir, la
recta tangente en x  0 .
De manera análoga se puede proceder para obtener un polinomio de cualquier grado que
aproxime a una función en x  0 . Realiza los mismos cálculos para obtener los coeficientes de
la parábola (polinomio de segundo grado) que mejor ajuste a la función en x  0 .
Aplica lo anterior para obtener la recta y la parábola que mejor aproximen a la función
y  7 x 2 log( x  3) en el punto x  0 .
y  f ( x) x0
p( x)  ax 2  bx  c
f (0)  r (0)  c
f '(0)  r '(0)  ax  b  b
f ''(0)  r ''(0) ?  2a
Rtg  f ''(0) x 2  f '(0) x  f (0)
y ( x)  7 x 2 log( x  3)
1
y '( x)  14 x log( x  3)  [7 x 2 ]log e
x3
log e 1
y ''( x)  14 log( x  3)  [14 x ]  log e[14 x  ]
x3 0 ( x  3) 2
0
y (0)  log 3
y '(0)  0
log 3 125
y ''(0)  14 log 3   log 3  6, 62
9 9
Rtg ( x)  2ax 2  bx  c
Rtg (0)  13, 25 x 2  log 3