1. El documento presenta una guía de estudio sobre límites y continuidad de funciones. Incluye 12 actividades con ejercicios para calcular límites, determinar la continuidad de funciones y relacionar límites con la continuidad. 2. Las actividades abarcan cálculo de límites algebraicos y gráficos, determinación de valores para que funciones sean continuas, y preguntas conceptuales sobre la relación entre límites y continuidad. 3. El documento provee una guía práctica para que estudiantes

1. UNIDADES TECNOLÓGICAS DE SANTANDER
GUÍA DE ESTUDIO 2
UNIDAD ACADÉMICA DEPARTAMENTO DE CIENCIAS BASICAS
ASIGNATURA: FUNDAMENTOS DE CALCULO DIFERENCIAL
UNIDAD TEMÁTICA LÍMITES Y CONTINUIDAD DE FUNCIONES
COMPETENCIA RESULTADOS DE APRENDIZAJE
Deducir resultados mediante
procesos de aproximación
Calcula el límite para las diferentes clases de funciones.
sucesiva, rangos de variación y
Interpreta el límite de una función en un contexto determinado.
límites en situaciones de
Determina la continuidad de funciones mediante los criterios de
medición.
continuidad
ACTIVIDADES DE APRENDIZAJE
R e a l i za r l a s a c t iv id a d es q u e a c o n t in u ac ió n s e e n u nc ia n t e n ie n d o e n cu en ta l a
c a r p e ta gu í a de A p un t e s d e l P r o fe s o r
ACTIVIDAD No 1
1. Resolver
a. En el siguiente ejercicio, completar la tabla y utilizar el resultado para estimar el límite
x2
lim
x 2 x x2
2
x 1,9 1,99 1,999 2,001 2,01 2,1
f(x)
x
b. Evaluar: f ( x)  en varios puntos próximos a x = 0 y usar el resultado para estimar
x 11
x
el límite lim
x 0 x 1 1
Completar la siguiente tabla
x -0,1 -0,01 -0,001 0 0,001 0,01 0,1
f (x)
Ing. Edgar Vargas Ruiz I- 2012 1

2. UNIDADES TECNOLÓGICAS DE SANTANDER
GUÍA DE ESTUDIO 2
2. Calcular los siguientes límites algebraicos:
x2  1 2x2  x  3 x3  8 x2 2
a ) lim b) lim c) lim d ) lim
x 0 x 1 x 1 x 1 x  2 x 2  11x  26 x 0 x
1 1

x2  x 2 x x 5  32
e) lim f ) lim g ) lim 2  x 2 h) lim
x 0 x 1 x 2
4  x2 x 0 x x 2 x2
x2  2x  3 x3 3 x 3  27 x2  1
i ) lim j ) lim k ) lim l ) lim
x 1 x2  5x  4 x 0
x2 2 x 3 x3 x 1 x3  1
3
x2  2x  7 x2  9 3x  1 x2  x  2  2
m) lim n) lim 2 o) lim p) lim
x 0
x2  7 x 3 x  x  12 x
1
9x2  1 x 1 x2  4x  3
3
x2  a2
q ) lim 2 (a  0)
x a x  2ax  a
2
4. Trace la grafica de una función y= f(x) que satisfaga las condiciones dadas (no es necesario que
incluya formulas, solamente marque los ejes coordenados y trace una grafica apropiada)
a. f (0)  0, f (1)  2, f (1)  2, lim f ( x)  1
x 
b. Su dominio es [0, 6] ; f (0) = f (2) = f (4) = f (6) = 2 ; f es continua, excepto para x = 2;
lim f ( x) 1 y lim f ( x)  3
x 2  x 5 
5. Calcule los límites:
2 x3  7 7 x3  2 x  1 x3  2 x 2
a. lim b. lim c. lim
x x3  x 2  x  7 x 4 x 4  3x 2  6 x x  5 x 2  x3  4
23 x 2 x4  3 9 x 2  3x  2 x
d. lim e. lim f. lim
x 2 x x 5 x3  7 x x 3x  5
ACTIVIDAD No 2
1. Encuentre el valor de h de modo que la función dada sea continua en x  1 , donde:
hx  3 si x 1
f ( x)  
5  hx si x 1
Ing. Edgar Vargas Ruiz I- 2012 2

3. UNIDADES TECNOLÓGICAS DE SANTANDER
GUÍA DE ESTUDIO 2
x si x  2
2. Hallar el valor de b para el cual la función f ( x)   es continua en todos los reales
2
bx si x  2
 
 1 si x0 
 
 1 
3. Sea f ( x)   si 0  x  1
 ax  b 
 
 
 5b si x 1 
Obtenga las constantes a y b de modo que f sea continua, y grafique esta función
4. Dada la función:
 2x 1 si x3 
 
f ( x)  ax  b si 3  x  5
 x2  2 x5 
 si 
Determine los valores de las constantes a y b para que f sea continua en todo su dominio.
5. Dada la función:
 3x  ab si x  3 
 
f ( x)  3ax  7b si 3  x  3
 x  12b x3 
 si 
Determine los valores de las constantes a y b para que f sea continua en todo su dominio.
6. Determine si el siguiente límite existe o no:
 x 2  1 x 2  10 
lím   
x   x  2 x 1 
 x5 si x  3 

 

7. Sea la función f ( x)   9  x 2 si 3  x  3 determinar:
 5 x si x3 

 

a. lim f ( x)  b. f (3)  c. f (3)  d . lim f ( x)  e. lim f ( x) 
x3 x 3
x3 
f ( x  h)  f ( x )
8. Dada la función f ( x)  2 x 2  4 x , hallar lim
h 0 h
Ing. Edgar Vargas Ruiz I- 2012 3

4. UNIDADES TECNOLÓGICAS DE SANTANDER
GUÍA DE ESTUDIO 2
a x 2 1
 x  x 1
2  x 2
9. Calcule el valor de a  para que se cumpla lim    e
x   x 
 
x
10. Grafique la función g ( x)  y calcule el lim g ( x)
x x0
f ( x) g ( x) f ( x)
11. Si x 1 1  x 2  4
lim y lim
x 1 1  x3
 2 Calcule el valor de lim
x 1 g ( x)


3
x si x  0

12. Sea la función g ( x)    hallar: a. La gráfica de g(x)

 x si x  0

b. lim g ( x)
x 0
ACTIVIDAD No 3
1. ¿Qué relación existe entre el límite de una función matemática para un determinado valor y la
continuidad de esa función en ese mismo punto? ¿Esa relación se cumple en todos los casos? ¿por
qué?
x 2  x  20
2. ¿Es 2 el valor del siguiente límite lim ? Justifique su respuesta.
x 5 x 5
3. ¿Es la función y  x 3  2 , continua en todo su dominio? Grafique para justificar su respuesta.
x2  9
4. ¿Qué puede decir de la continuidad de la función y ? Qué pasa cuando x = - 3? Se
x3
puede argumentar que la gráfica es una línea recta? Explique
5. ¿Qué métodos conoce para calcular el límite de una función? Aplique esos procesos y trate de
obtener el límite en cada caso, sino existe límite, diga `por qué.
x2  4 x 2  x  12 x 1
a. lim b. lim 2 c. lim
x 2 x  2 x 3 x  5 x  6 x 1 x 3 2
2
x3  4 x  1 1 1
d. lim e. lim f. lim
x 1 x 2 x x
1
x
1 x 0 2x
2 2
( x  h)3  x 3 1 x  x2
g. lim h. lim i. lim
h 0 h x  2x x 0  x
Ing. Edgar Vargas Ruiz I- 2012 4

5. UNIDADES TECNOLÓGICAS DE SANTANDER
GUÍA DE ESTUDIO 2
6. Encontrar el valor de a ( a  ) de modo que lim f ( x) exista, si
x1
 x3  a3 
 si x  1
 xa 
f ( x)   
 x3 a
x  1
3
si

 xa 

7. En los siguientes problemas, establezca si la función indicada es continúa o no en su dominio, si no
lo es, explique porqué y diga la clase de discontinuidad que presenta:
8
a. f  x   4 x 2  2 x  12 b. f  x   c. g  x   x  3
x2
t3  8  x  3 si x  2  x  3 si x  3

d. g t   e. f  x    2 f . f  x  
t 2  x  1 si x  2 2
 si x  3
t3  8
 si t  2 3  x si x  1
g. h  t    t  2 h. g  x   
 12 si t  2 3  x si x  1

 2x2  x  3
 si x  1 4
i. f  x    x  1 j. g  x  
 x  3
2
 si x 1
 2
ACTIVIDAD No 4
1. Representar las funciones siguientes e indicar si tiene algún punto de discontinuidad:
x  1 si x  3 x  1 si x  1
 
f ( x )  x 2 si 3  x < 4 f ( x)   x 2  1 si 1 < x  2
0  2
 si x  4 x si x  2
2. Estudiar la continuidad de las siguientes funciones:
x 1 x2  5x  6  x  1 si x  0
1. f ( x)  2. f ( x)  3. f ( x)  
x2 1 x2  x  1 si x  0
2  x 2 si x  2
4. f ( x)  4  x 2
5. f ( x)   6. f ( x)  x 2  1
2 x  6 si x  2
1 2 x  1 si x   4, 2 
 si x  1 
7. f ( x)   x 8. f ( x)  x  x 9. f ( x)  1  3x si x   2,1
 x 1  2
 si x  1
 x si x  1,5
Ing. Edgar Vargas Ruiz I- 2012 5

6. UNIDADES TECNOLÓGICAS DE SANTANDER
GUÍA DE ESTUDIO 2
x2 1
3. Probar que la función f ( x)  no es continua en x = 1 e indicar que tipo de
x3  7 x  8
discontinuidad presenta en dicho punto.
4. Al estudiar la continuidad de la función:
( x  1) 2 si x  0
h( x )  
( x  1) si x  0
2
Se puede afirmar que:
A. h(x) es continua en toda la recta real
B. h(x) es discontinua en x = 0
C. La función tiene una discontinuidad removible(evitable) en x = 0
D. La función es discontinua únicamente en el intervalo [- 1, 1]
5. Con relación a la gráfica que aparece a continuación, una de las siguientes afirmaciones es falsa
(justifique la respuesta)
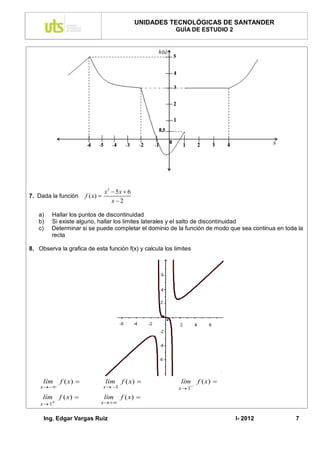
6. Sea h(x) una función cuya gráfica se adjunta:
Indique:
a) lim h(x) b) lim h(x) c) lim h(x)
x  6 x  2 x 1 
d) lim h(x) e) lim h(x) f) lim h(x)
x 1 x 1 x 4
g) lim h(x) h) lim h(x)
x  6  x  6 
Ing. Edgar Vargas Ruiz I- 2012 6

7. UNIDADES TECNOLÓGICAS DE SANTANDER
GUÍA DE ESTUDIO 2
x2  5x  6
7. Dada la función f ( x) 
x2
a) Hallar los puntos de discontinuidad
b) Si existe alguno, hallar los limites laterales y el salto de discontinuidad
c) Determinar si se puede completar el dominio de la función de modo que sea continua en toda la
recta
8. Observa la grafica de esta función f(x) y calcula los limites
lím f ( x)  lím f ( x)  lím f ( x) 
x  x 1 x 1
lím f ( x)  lím f ( x) 
x 1 x 
Ing. Edgar Vargas Ruiz I- 2012 7

8. UNIDADES TECNOLÓGICAS DE SANTANDER
GUÍA DE ESTUDIO 2
ACTIVIDAD No 5
Resuelva los siguientes problemas de aplicación de limites y continuidad
1. Si el costo total de producción de q artículos en una industria está dado por C  7000  10q ,
encontrar el costo promedio, cuando el nivel de producción crece continuamente.
18000
2. La población p de una ciudad en t años está dada por p  50000  . Encontrar la población a
 t  3
2
largo plazo
3. Para una relación particular de huésped-parásito, si x representa la densidad de huéspedes, es decir
el número de huéspedes por unidad de área y f(x) representa el número de parásitos en un
1000 x
determinado período, entonces f ( x)  . Encontrar a qué valor se aproximaría el número de
12  40 x
parásitos, si la densidad de huéspedes aumentara sin cota.
4. El costo c, en pesos, por enviar un paquete es de 50 pesos si pesa hasta 5 kilogramos, de 80 pesos si
su peso es mayor de 5 y hasta 10 kilogramos, y de (x + 70) pesos si pesa más de 10 y hasta 50
kilogramos. Expresar la función del costo, analizar en qué puntos tiene discontinuidades y trazar su
gráfica.
5. La tarifa telefónica de larga distancia entre dos ciudades es de $15 los primeros 3 minutos y de
$(t + 20), para las llamadas de más de tres minutos. Expresar la función de la tarifa telefónica,
analizar si hay puntos de discontinuidad y trazar su gráfica.
EVALUACIÓN
Límites y continuidad
 1 1  1 
1. En un examen, a Lorenzo se le pide que calcule lim     . Lorenzo responde: “puesto
x 4  x 4  x  4 
1 1 
que lim     0 por tanto, por el teorema del producto, el resultado es cero”. Diga si Lorenzo
x 4 x 4
está en lo cierto; en caso de estar equivocado, obtenga el límite correcto.
2. Complete la expresión de manera que el procedimiento sea correcto:
x 4  8x 2  9 ( x 2  9)( ) ( x  3)( )( )
lim  lim  lim  60
x 3 x3 x 3 x3 x 3 x3
3. Trace la gráfica de un ejemplo de una función f que satisfaga todas las condiciones dadas:
lim f ( x )  4, lim f ( x )  2, lim f ( x )  2, f (3 )  3, f ( 2 )  1
x 3  x 3 x  2
Ing. Edgar Vargas Ruiz I- 2012 8

9. UNIDADES TECNOLÓGICAS DE SANTANDER
GUÍA DE ESTUDIO 2
4. Evalúe los siguientes límites, si existen:
 3z, z  1 a5  b5  3x 8 
a) lim f ( z ) si f ( z )   b) lim c) lim   
z 1
 3, z  1 a b ab x  4x 4 x 4
  x2 si x  1

 3 si x  1
5. Determine si f ( x )   es continua en todo su dominio. Si no lo es,
2  x si 1  x  1

 1 si x 1
 x2
determine si la discontinuidad es evitable o no evitable.
6. Obtenga las constantes a y b, si existen, de modo que la función f sea continua en los reales.
 3 6 x 2
 si x  2
 x2
 1
f ( x)   si 2  x  5
 ax  b


 3 si x  5
w2  1
7. Diga en qué puntos es continua la función H(w ) 
(w  8 )3
x4 3
8. ¿Qué se necesitaría para que la función f ( x )  sea continua en x = 5?
x 5
9. Dadas las siguientes funciones:
a) Hallar su dominio de definición.
b) Calcular los límites indicados.
x2
1. f ( x )  2 lim f ( x)
x 4 x2
25  x 2
2. f ( x )  lim f ( x)
x5 x5
x 4  3 x3  2 x 2
3. f ( x )  lim f ( x )
x3  x 2 x0
x3  3 x 2  2 x
4. f ( x )  lim f ( x )
x2  4 x  3 x 1
Ing. Edgar Vargas Ruiz I- 2012 9

10. UNIDADES TECNOLÓGICAS DE SANTANDER
GUÍA DE ESTUDIO 2
x 4  16
5. f ( x )  lim f ( x )
x2  x  6 x2
10. A partir de la gráfica determinar:
a) lim f ( x) b) lim f ( x ) c) lim f ( x )
xa
x  a x  a
(v) (vi) (vii)
11. A partir de las siguientes gráficas, determinar si las funciones son continuas en x 0. De no serlo,
indicar cuál de las tres condiciones no se cumple:
Ing. Edgar Vargas Ruiz I- 2012 10

11. UNIDADES TECNOLÓGICAS DE SANTANDER
GUÍA DE ESTUDIO 2
BIBLIOGRAFÍA
 APUNTES DEL DOCENTE DESIGUALDADES
 STEWART James , calculo conceptos y aplicaciones, Editorial Thomson
 HOFFMANN, BRADLEY, ROSEN, Cálculo Aplicado para administración, economía y ciencias sociales. Mc
Graw-Hill
 HARSHBARGER, REYNOLDS, Matemáticas Aplicada a la administración, economía y ciencias sociales. Mc
Graw-Hill
Ing. Edgar Vargas Ruiz I- 2012 11