Este documento presenta el proyecto final de cálculo de un estudiante de ingeniería industrial. Contiene 12 problemas resueltos sobre cálculo que incluyen determinar dominios de funciones, calcular límites, derivadas e integrales indefinidas y definidas. También incluye gráficas de funciones de oferta y demanda y la determinación de su punto de equilibrio.

1. Nombre asignatura :Cálculo
Proyecto Final
Nombre del estudiante:
Fecha de entrega: 20/08/2023
Carrera: Ingeniería Industrial
EVALUACIÓN

2. 2
EVALUACIÓN
DESARROLLO:
1. Determina el dominio de la función
𝑓(𝑥) = √
𝑥 − 2
𝑥 − 1
𝑥 − 2
𝑥 − 1
≥ 0
𝑥 − 2 ≥ 0
𝑥 ≥ 2
𝑥 − 1 > 0
𝑥 > 1
𝐷𝑓 = [1, 2[
2. Dada las graficas de funciones y =f(x) e y= g(x) , calcula el valor de :
(f*g)(-1) +(g *f)(0)

3. 3
EVALUACIÓN
𝑓 (𝑥) = (𝑥 − 𝑦)
𝑔 (𝑥) = (−𝑥 + 3𝑦)
(𝑓 ∗ 𝑔)(−1) + (𝑔 ∗ 𝑓)(0)
((𝑥 − 𝑦) ∗ (−𝑥 + 3𝑦)) + (−1) + ((−𝑥 + 3𝑦) ∗ (𝑥 − 𝑦))(0)
((𝑥2
+ 3𝑥𝑦 − 𝑥𝑦 − 3𝑦2)(−1)) + (−𝑥2
− 𝑥𝑦 + 3𝑥𝑦 − 3𝑦2)(0)
−𝑥2
− 3𝑥𝑦 + 𝑥𝑦 + 3𝑦2
−𝑥2
− 2𝑥𝑦 + 3𝑦2
3. Calcula el siguiente límite
lim
𝑥→1
=
𝑥2
+ 2𝑥 − 3
𝑥2 − 𝑥
lim
𝑥→1
=
(𝑥 + 3)(𝑥 − 1)
𝑥(𝑥 − 1)
lim =
𝑥→1
(𝑥 + 3)
𝑥
lim
𝑥→1
=
(1 + 3)
1
lim
𝑥→1
=
4
1
lim =
𝑥→1
4
4. Calcula el siguiente límite
lim
𝑥→0
=
𝑥
√𝑥 + 1 − 1
lim
𝑥→0
=
𝑥
√𝑥 + 1 − 1
∗
√𝑥 + 1 − 1
√𝑥 + 1 − 1
lim
𝑥→0
=
𝑥(√𝑥 + 1 − 1)
(√𝑥 + 1)
2
− 12
lim
𝑥→0
=
𝑥(√𝑥 + 1 − 1)
(𝑥 + 1) − 1

4. 4
EVALUACIÓN
lim
𝑥→0
=
√𝑥2 + 1 − 1
(𝑥 + 1) − 1
lim
𝑥→0
=
(𝑥 + 1) − 1
(𝑥 + 1) − 1
lim
𝑥→0
=
(0 + 1) − 1
(0 + 1) − 1
lim
𝑥→0
=
1 − 1
1 − 1
lim
𝑥→0
= 0
5. Para la función
𝑓(𝑥) = 𝑥2
ln(𝑥)
Se pide determinar el valor de f’ (e)
𝑓(𝑥) = 𝑥2
ln(𝑥)
𝑓(𝑒) = 𝑒2
ln(𝑒)
𝑓′(𝑒) = 2𝑒 ∗ 1
𝑓′(𝑒) = 2𝑒
6. Para la función
𝑓(𝑥) =
2
𝑥2 + 4
Se pide determinar el valor de f’’(0)
𝑓(𝑥) =
2
𝑥2 + 4
𝑓′(𝑥) =
(𝑑𝑥)(𝑥2
+ 4) − (2)(2𝑥)
(𝑥2 + 4)2
𝑓`(𝑥) =
(𝑑𝑥)(𝑥2
+ 4) − (2)(2𝑥)
(𝑥2 + 4)2
𝑓′(𝑥) =
𝑥3
+ 4𝑥 − 4𝑥
(𝑥2 + 4)2

5. 5
EVALUACIÓN
𝑓′(𝑥) =
𝑥3
(𝑥2 + 4)2
𝑓`(𝑜) =
𝑥3
(𝑥2 + 4)2
𝑓′′(𝑜) =
3𝑥2
4𝑥(𝑥2 + 4)
𝑓′′(𝑜) =
3 ∗ 02
4 ∗ 0(02 + 4)
𝑓′′(𝑜) = 0
7. En una fábrica se determinó que el ingreso dado por I(x)=23000x-0,8x^2 pesos, cuando se
venden x unidades de cierto articulo al mes. Actualmente, se producen 175 unidades y se
planea incrementar la producción en una unidad.
Usa derivadas para aproximar el ingreso que se genera al producir la unidad 176
𝐼(𝑥) = 2300𝑥 − 0,8𝑥2
 Ingreso marginal
𝐼(𝑥) = 2300𝑥 − 0,8𝑥2
𝐼′(𝑥) = 2300 − 1,6𝑥
 Evaluación de la derivada para producir la unidad 175
𝐼′(175) = 2300 − 1,6(175)
𝐼′(175) = 2300 − 280
𝐼′(175) = 2020
El ingreso que se genera al producir 175 unidades es de $2020 app.
 Ingreso al producir la unidad 176
𝐼 = 𝐼(𝑥 + 1) − 𝐼(𝑥)
𝐼 = 2300(𝑥 + 1) − 0,8(𝑥 + 1)2
− (2300𝑥 − 0,8𝑥2
)
𝐼 = 2300 + 2300𝑥 − 0,8(𝑥 + 1)2
− 2300𝑥 − 0,8𝑥2
𝐼 = 2300 − 0,8(𝑥 + 1)2
− 0,8𝑥2
𝐼 = 2300 − 0,8(𝑥2
+ 2𝑥 + 1 − 𝑥2
)
𝐼 = 2300 − 0,8(2𝑥 + 1)
𝐼 = 2300 − 1,6𝑥 + 0,8
𝐼 = 2299,2 − 1,6𝑥

6. 6
EVALUACIÓN
 Sustituir la unidad 176 en la expresión
𝐼 (𝑥) = 2299,2 − 1,6𝑥
𝐼(176) = 2299,2 − 1,6𝑥
𝐼(176) = 2299,2 − 1,6(176)
𝐼(176) = 2299,2 − 281,6
𝐼(176) = 2017,6 ≅ 2018
El ingreso al producir la unidad 176 es de $2018.
8. Determina los intervalos de crecimiento y de decrecimiento de la función:
𝑓(𝑥) = 𝑥3
− 3𝑥 + 2
a) Puntos críticos:
𝑓(𝑥) = 𝑥3
− 3𝑥 + 2
𝑓′(𝑥) = 3𝑥2
− 3
b) Sustituir f’(0) para encontrar puntos críticos
𝑓′(𝑥) = 3𝑥2
− 3
0 = 3𝑥2
− 3
3 = 3𝑥2
3/3 = 𝑥2
1 = 𝑥2
√1 = 𝑥
1 = 𝑥
𝑓′(𝑥) = 3𝑥2
− 3
0 = 3𝑥2
− 3
−3𝑥2
= −3
𝑥2
= −3 /−3
𝑥2
= −1
𝑥 = √−1
𝑥 = −1
Por lo tanto los puntos críticos son :
X=1
X=-1
c) Determinar los intervalos alrededor del punto crítico:
(−∞, −1), (−1,1), (1, +∞)

7. 7
EVALUACIÓN
d) Escoger un punto para cada intervalo
Intervalo Punto 𝑓′(𝑥) = 3𝑥2
− 3
(−∞, −1), -2 9 - + D C
(−1,1) 0 -3 + - C D
(1, +∞) 2 9 + + D C
9. Para la función determina:
𝑓(𝑥) = 𝑥3
− 3𝑥 + 2
El máximo relativo está en x=-1
El mínimo relativo está en x=1
a) El valor x donde la función alcanza un mínimo y cuál es ese valor mínimo
𝑓(𝑥) = 𝑥3
− 3𝑥 + 2
𝑓(1) = 13
− 3 ∗ 1 + 2
𝑓(1) = 0
El mínimo que alcanza la función es 0 en x=1
b) El valor x donde la función alcanza un máximo y cuál es ese valor máximo.
𝑓(𝑥) = 𝑥3
− 3𝑥 + 2
𝑓(−1) = −13
− 3 ∗ −1 + 2
𝑓(−1) = 4
El máximo relativo que alcanza la función es 4 en x=-1

8. 8
EVALUACIÓN
10. La demanda de un artículo que produce una compañía varía con el precio que esta cobra por
el artículo. La compañía determino que los ingresos totales anuales, en miles de pesos, son
una función del precio p, en pesos, dada por la expresión:
𝐼(𝑝) = −50𝑝2
+ 500𝑝
Resolver derivada
𝐼(𝑝) = −50𝑝2
+ 500𝑝
𝐼′(𝑝) = −100𝑝 + 500
a) Determine el precio que debe cobrarse con el fin de maximizar los ingresos totales.
𝐼′(𝑝) = −100𝑝 + 500
0 = −100𝑝 + 500
100𝑝 = 500
𝑝 =
500
100
𝑝 = 5
El precio que debe cobrarse es de $5 pesos
b) ¿Cuál es el valor de esos ingresos totales?
𝐼(𝑝) = −50𝑝2
+ 500𝑝
𝐼(5) = −50𝑝2
+ 500𝑝
𝐼(5) = −50(5)2
+ 500(5)
𝐼(5) = 1250
El ingreso total es de $1250
11. Calcula la siguiente integral indefinida
∫ (2𝑒3𝑥
− 3𝑥2
+
1
𝑥
−
5
4
) 𝑑𝑥
∫ 2𝑒3𝑥
𝑑𝑥 − 3𝑥2
𝑑𝑥 +
1
𝑥
𝑑𝑥 −
5
4
𝑑𝑥
2 ∫ 𝑒3𝑥
𝑑𝑥 − 3 ∫ 𝑥2
𝑑𝑥 + ln 𝑥 −
5
4
∫ 𝑑𝑥
2 ∗
𝑒3𝑥
3
− 3 ∗
𝑥3
3
+ ln 𝑥 −
5
4
∗ 𝑥 + 𝑐
2𝑒3𝑥
3
− 𝑥3
+ ln 𝑥 −
5
4
𝑥 + 𝑐

9. 9
EVALUACIÓN
12. Calcula la siguiente integral indefinida
∫
𝑥2
− 𝑥 + 6
𝑥3 + 3𝑥
𝑑𝑥
∫
𝑑𝑢
𝑢
∫𝑙𝑛| 𝑢| + 𝑐
∫ ln|𝑥2
− 𝑥 + 6| + 𝑐
13. Calcula la siguiente integral definida
∫ 𝑥𝑒𝑥2
1
0
𝑑𝑥
1
2
∫ 𝑥𝑒𝑥2
1
0
𝑑𝑥
1
2
𝑥𝑒𝑥2
|
1
0
1
2
1𝑒12
−
1
2
0𝑒02
1
2
𝑒 −
1
2
𝑒 − 1
2
14. Calcula la siguiente integral definida
∫ 2𝑥𝑒4𝑥
1
0
𝑑𝑥
2
𝑥2
2
∗
1
4
𝑒4𝑥
|
1
0
𝑥2
∗
1
4
𝑒4𝑥
|
1
0

10. 10
EVALUACIÓN
(12
) (
1
4
𝑒4∗1
) − (02
) (
1
4
𝑒4∗0
) −
1
4
𝑒4
15. Para las siguientes funciones oferta y demanda, respectivamente,
𝑝 = 𝑆(𝑞) = 52 + 2𝑞
𝑝 = 𝐷(𝑞) = 100 − 𝑞2
Se pide determinar :
a) El grafico que muestre la situación entre las funciones de oferta y demanda

11. 11
EVALUACIÓN
b) El punto de equilibrio entre la oferta y la demanda
52 + 2𝑞 = 100 − 𝑞2
52 + 2𝑞 − 100 + 𝑞2
= 0
𝑞2
+ 2𝑞 + 48 = 0
𝑝 =
−𝑏 ± √𝑏2 − 4𝑎𝑐
2𝑎
𝑝 =
−2 ± √22 − 4 ∗ 1 ∗ 48
2 ∗ 1
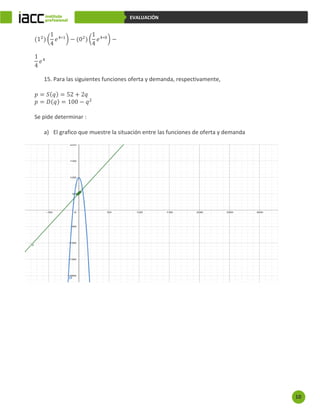
𝑝 =
−2 ± √188
2
𝑝 =
−2 ± 13,71
2
𝑝 =
−2 ± 13,71
2
𝑝1 =
−2 − 13,71
2
= −7,85 ≅ −8
𝑝2 =
−2 + 13,71
2
= 5,85 ≅ 6
Se debe considerar el valor positivo al ser una cantidad
𝑆(𝑞) = 52 + 2𝑞
𝑆(6) = 52 + 2 ∗ 6
𝑆(6) = 64
c) El excedente del productor
𝐸𝑝 = ∫[(𝑝(𝑜)) − (𝐷(𝑞))]𝑑𝑥
6
0
𝐸𝑝 = ∫[64 − (100 − 𝑞2)]𝑑𝑥
6
0
𝐸𝑝 = [64dx − (100𝑑𝑥 − 𝑞2
𝑑𝑥)]|
6
0
𝐸𝑝 = [64 − 100 −
𝑞3
3
]|
6
0

12. 12
EVALUACIÓN
𝐸𝑝 = [−
𝑞3
3
− 36]|
6
0
Ep = (−
63
3
− 36) − (−
03
3
− 36)
Ep = 72
El excedente del productor es 72u.m
d) El excedente del consumidor.
𝐸𝑐 = ∫[(𝑆(𝑞)) − (𝑝(𝑜))]𝑑𝑥
6
0
𝐸𝑐 = ∫ [(52 + 2𝑞) − (64)]𝑑𝑥
6
0
𝐸𝑐 = ∫ [52 + 2q − 64]𝑑𝑥
6
0
𝐸𝑐 = ∫ [2q − 14]𝑑𝑥
6
0
𝐸𝑐 = 2
𝑞2
2
− 14|
6
0
𝐸𝑐 = (𝑞2
− 14) − (𝑞2
− 14)|
6
0
𝐸𝑐 = (62
− 14) − (02
− 14)|
𝐸𝑐 = 36
El excedente del consumidor es 36u.m

13. 13
EVALUACIÓN
REFERENCIAS BIBLIOGRÁFICAS
IACC. (2023). Composición y gráfico de funciones. Cálculo. Semana 1
IACC. (2023). Límites laterales e infinitos. Cálculo I. Semana 2
IACC. (2023). Interpretación gráfica y continuidad de límites. Cálculo I. Semana 3
IACC. (2023). Conceptos de derivadas. Cálculo. Semana 4
IACC. (2023). Derivadas de orden superior. Cálculo. Semana 5
IACC. (2023). Aplicaciones de derivadas. Cálculo. Semana 6
IACC. (2023). Conceptos integrales. Cálculo. Semana 7
IACC. (2023). Aplicaciones de integrales. Cálculo. Semana 8