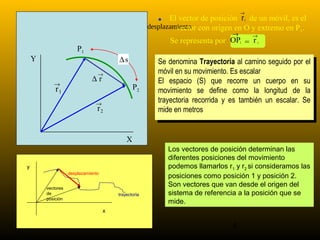
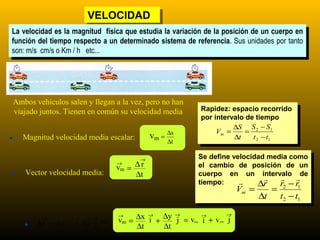
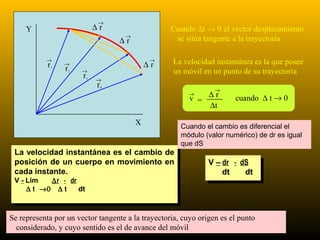
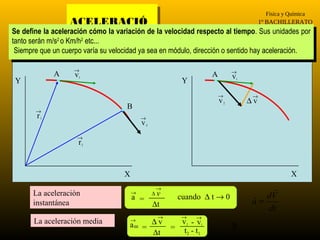
1) La cinemática estudia el movimiento sin considerar las causas que lo producen. 2) El movimiento y el reposo son conceptos relativos que dependen del sistema de referencia elegido. 3) Para describir completamente un movimiento se debe indicar respecto a qué sistema de referencia se realizaron las mediciones.