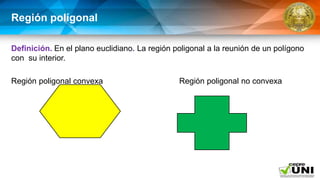
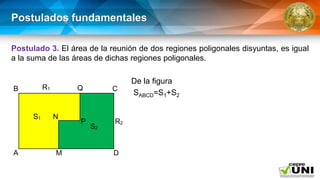
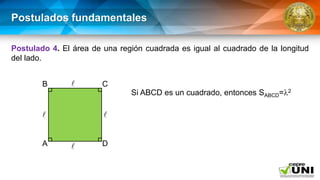
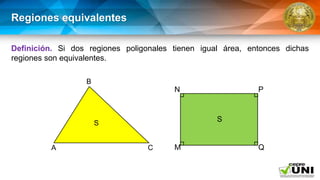
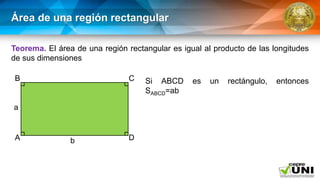
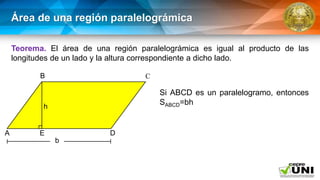
El documento aborda la geometría de áreas de regiones poligonales, definiendo una región poligonal como la unión de un polígono y su interior. Presenta postulados fundamentales sobre el cálculo del área, incluyendo la congruencia de triángulos y la suma de áreas de regiones disyuntas. También se describen teoremas específicos para calcular el área de figuras como cuadrados, rectángulos y paralelogramos.

1. GEOMETRÍA

2. Áreas de regiones polígonales

3. Región polígonal
Definición. En el plano euclidiano. La región poligonal a la reunión de un polígono
con su interior.
Región poligonal convexa Región poligonal no convexa

4. Postulados fundamentales
S
1 2 3 n
PP P P
S
Postulado 1. A toda región poligonal le corresponde un único
número real positivo. Dicho número se denomina área de la región
poligonal.
Notación:
Sea P1P2P3..Pn un polígono entonces el área de región
poligonal correspondiente se denota como
S es un número
real mayor que 0.

5. Postulados fundamentales
Postulado 2. Si dos triángulos son congruentes, entonces las áreas de las
regiones correspondientes son iguales.
Si ABCDEF, entonces SABC=SDEF
F
A C
B
D
E
S S

6. Postulados fundamentales
Postulado 3. El área de la reunión de dos regiones poligonales disyuntas, es igual
a la suma de las áreas de dichas regiones poligonales.
De la figura
SABCD=S1+S2
A
B C
D
M
N
P
Q
S2
S1
R1
R2

7. Postulados fundamentales
Postulado 4. El área de una región cuadrada es igual al cuadrado de la longitud
del lado.
Si ABCD es un cuadrado, entonces SABCD=2
A
B
D
C

8. Regiones equivalentes
Definición. Si dos regiones poligonales tienen igual área, entonces dichas
regiones son equivalentes.
A
B
S
C M
N
Q
P
S

9. Área de una región rectangular
Teorema. El área de una región rectangular es igual al producto de las longitudes
de sus dimensiones
Si ABCD es un rectángulo, entonces
SABCD=ab
A
B
D
C
a
b

10. Área de una región paralelográmica
Teorema. El área de una región paralelográmica es igual al producto de las
longitudes de un lado y la altura correspondiente a dicho lado.
Si ABCD es un paralelogramo, entonces
SABCD=bh
C
A D
B
b
E
h