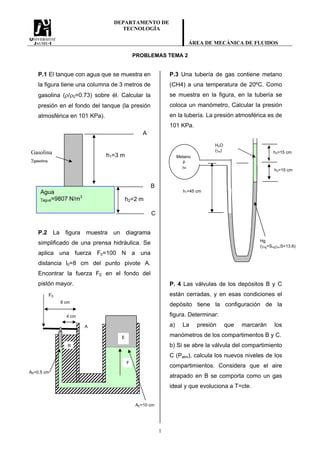
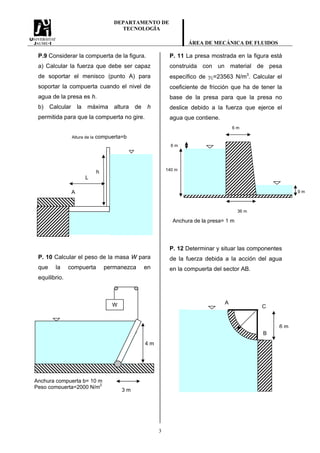
El documento presenta 12 problemas de mecánica de fluidos relacionados con presiones, fuerzas y equilibrio en sistemas que contienen líquidos y gases. Los problemas involucran tanques, tuberías, manómetros, compuertas y estructuras sumergidas en agua, y piden calcular presiones, fuerzas, alturas y pesos para determinar estados de equilibrio.

1. DEPARTAMENTO DE
TECNOLOGÍA
ÁREA DE MECÁNICA DE FLUIDOS
1
PROBLEMAS TEMA 2
P.1 El tanque con agua que se muestra en
la figura tiene una columna de 3 metros de
gasolina (ρ/ρ0=0.73) sobre él. Calcular la
presión en el fondo del tanque (la presión
atmosférica en 101 KPa).
P.2 La figura muestra un diagrama
simplificado de una prensa hidráulica. Se
aplica una fuerza F0=100 N a una
distancia l0=8 cm del punto pivote A.
Encontrar la fuerza FE en el fondo del
pistón mayor.
P.3 Una tubería de gas contiene metano
(CH4) a una temperatura de 20ºC. Como
se muestra en la figura, en la tubería se
coloca un manómetro, Calcular la presión
en la tubería. La presión atmosférica es de
101 KPa.
P. 4 Las válvulas de los depósitos B y C
están cerradas, y en esas condiciones el
depósito tiene la configuración de la
figura. Determinar:
a) La presión que marcarán los
manómetros de los compartimentos B y C.
b) Si se abre la válvula del compartimiento
C (Patm), calcula los nuevos niveles de los
compartimientos. Considera que el aire
atrapado en B se comporta como un gas
ideal y que evoluciona a T=cte.
Agua
γagua=9807 N/m3
h1=3 m
h2=2 m
A
B
C
Gasolina
γgasolina
A
F0
8 cm
4 cm
B
AB=0.5 cm
E
F
AE=10 cm
Metano
p
γM
H2O
(γw)
h2=15 cm
h3=15 cm
h1=45 cm
Hg
(γHg=SHgγw;S=13.6)

2. DEPARTAMENTO DE
TECNOLOGÍA
ÁREA DE MECÁNICA DE FLUIDOS
2
P.5 Con la intención de medir la caída de
presión entre los puntos A y B de una
tubería, se coloca un manómetro
diferencial de mercurio, tal y como se
muestra en la figura. Calcular cual será la
caída de presión (PA-PB) si la diferencia
entre las ramas del manómetro es h.
P.6 En la figura se muestra un depósito
abierto que contiene dos líquidos
diferentes inmiscibles, calcular:
a) Altura del líquido en el manómetro A.
b) Altura del líquido en el manómetro B.
c) Presión total en el fondo del depósito.
P.7 Calcular el valor de F para que se
mantenga la compuerta.
P.8 Determinar el peso del contrapeso
para mantener cerrada la compuerta.
0.3 m
5 m
2 m1.5 m
3 m
A
B
C
1 m
A . . B
h
agua
mercurio
2 m
A B
Líquido A
γA=0.72γagua
Líquido B
γB=2.36γagua
1 m
F
Anchura: 1 m
4 m
Anchura: 5 m
W 3 m

3. DEPARTAMENTO DE
TECNOLOGÍA
ÁREA DE MECÁNICA DE FLUIDOS
3
P.9 Considerar la compuerta de la figura.
a) Calcular la fuerza que debe ser capaz
de soportar el menisco (punto A) para
soportar la compuerta cuando el nivel de
agua de la presa es h.
b) Calcular la máxima altura de h
permitida para que la compuerta no gire.
P. 10 Calcular el peso de la masa W para
que la compuerta permanezca en
equilibrio.
P. 11 La presa mostrada en la figura está
construida con un material de pesa
específico de γC=23563 N/m3
. Calcular el
coeficiente de fricción que ha de tener la
base de la presa para que la presa no
deslice debido a la fuerza que ejerce el
agua que contiene.
P. 12 Determinar y situar las componentes
de la fuerza debida a la acción del agua
en la compuerta del sector AB.
4 m
h
Altura de la compuerta=b
L
A
Anchura compuerta b= 10 m
Peso compuerta=2000 N/m2
W
3 m
9 m
6 m
140 m
36 m
6 m
Anchura de la presa= 1 m
A
C
B
6 m

4. DEPARTAMENTO DE
TECNOLOGÍA
ÁREA DE MECÁNICA DE FLUIDOS
4
P. 13 La compuerta de peso P tiene una
configuración cilíndrica de radio R y
longitud L. Calcular la tensión T a aplicar
para levantarla en los casos en que el
nivel esté en A y en B.
P. 14 Suponer que tenemos una taza de
simetría cilíndrica que introducimos poco a
poco en un depósito de agua de forma
que el aire quede encerrado en ella.
Calcular la expresión de y en función de H
y h.
P. 15 Una canoa de simetría cilíndrica con
una longitud de 5.25 m y un radio exterior
de 0.35 m flota sobre un río con una
profundidad d. Calcular el peso máximo
que puede soportar la canoa sin tocar el
fondo o hundirse.
P. 16 Suponer que la esfera de la figura
está flotando en un estanque. Calcular:
a) Peso especifico de la esfera.
b) Nueva posición de la esfera si quitamos
el peso.
P. 17 Calcular el porcentaje que se ve de
un iceberg.
P. 18 ¿A que velocidad subirá una burbuja
de hidrógeno en el interior de un depósito
de agua?
Suponer que la burbuja tiene un diámetro
de 0.025 mm y que la fuerza de oposición
del agua al movimiento de la burbuja
viene dada por la expresión FD=3πµVd;
donde m es la viscosidad del agua, y V y d
son la velocidad y diámetro de la burbuja
respectivamente.
T
R
NIVEL A
NIVEL B 20 Kg
1 m3
agua
H-y
y
agua h
D