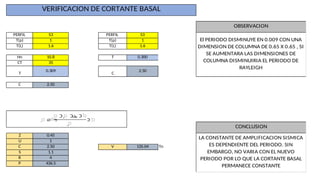
El documento presenta un análisis sísmico estático de un edificio de vivienda en Chiclayo y otro de oficina en Trujillo, utilizando modelos de corte y la norma E-030. Se calculan fuerzas cortantes en la base, desplazamientos elásticos e inelásticos y se determinan los tamaños necesarios de columnas para cumplir con las máximas permitidas. Se discuten irregularidades estructurales y la variación del periodo fundamental en respuesta a cambios en las dimensiones de las columnas.

1. HUAYAMA ZURITA SHEYLY YULIAR
TEVES ADANAQUE DANIEL AARON
ANÁLISIS SÍSMICO
ESTÁTICO
EJERCICIOS

2. EJERCICIO 01
La figura muestra la planta (12mx15m) y la elevación de un edificio de vivienda que se construirá en
la ciudad de Chiclayo sobre suelo S3. Se desea hacer un análisis preliminar de desplazamiento en la
dirección x-x usando un modelo traslacional de corte, empleando las fuerzas del método estático de
la norma E-030 y disponiendo que todos los elementos no estructurales se construirán aislados de la
estructura. La carga muerta de los 2 primeros pisos es 0.80 ton/m2 y en la azotea 0.70 tn/m2. La
carga viva en los 2 primeros pisos es de 0.20 ton/m2 y en la azotea es de 0.10 ton/m2.
Considere . Las columnas son todas iguales y cuadradas de lado “c”.

3. MODELADO DEL PORTICO 3D

4. A) Determinar la fuerza cortante en la base y la distribución de las
fuerzas. Determine el periodo con la expresión .
B) Calcule los desplazamientos elásticos e inelásticos de los 3 niveles
, en función del lado de las columnas “c”
C) Calcule el tamaño de la columna para que las derivas del edificio
no sobrepase los valores máximos definidos en la norma.
D) Partiendo de las fuerzas halladas en (A), calcule el periodo
fundamental en X-X empleando la expresión de Rayleigh. Con este
nuevo periodo ¿Cambiará la fuerza cortante basal?

5. A) Determinar la fuerza cortante en la base y la distribución
de las fuerzas. Determine el periodo con la expresión .
PASO 1
Para calcular el cortante basal de la estructura, debemos conocer los siguientes factores:
Z= factor de zona
U= factor de uso
C= factor de amplificación sísmica
S= factor de suelo
R= coeficiente de reducción de las fuerzas sísmicas
P= peso sísmico
DESARROLLO

6. Según el problema la vivienda se construirá en la ciudad de
Chiclayo sobre suelo S3.
Nos dirigimos a la Norma E-030, para poder tomar los valores
correspondientes
Z=0.45
S=1.10
PASO 2

7. PASO 3: Cálculo del factor “C”

8. 3.1. Hallaremos , ya que estos datos nos servirán para
encontrar el factor de amplificación sísmica (C)
=1
=1.6

9. 3.2. Hallaremos
hn 10.8
CT 35
T 0.309

10. 3.3. Después de haber calculado Tp, TL, y T, vamos a definir
el factor de amplificación sísmica.
• =1
• =1.6
• T =0.309
T<Tp
0.309<1, C=2.5

11. IRREGULARIDADES DE ALTURA
DATOS
GENERALES
- N° de columnas por piso : 12 COLUMNAS
- E = 2200000 Ton/m2
- Dimensiones de la columna cuadrada : C X C
- Rigidez de columnas articuladas
- Rigidez de columnas empotradas
- Inercia de columna

12. IRREGULARIDADES DE ALTURA
IRREGULARIDADES EXTREMA DE RIGIDEZ
PISO CONSTANTE
1 C^4
2 C^4
3 C^4
RIGIDEZ DE
ENTREPISO(ki)
120279.92
615743.44
0.20
1
OBSERVACION
EXISTE IRREGULARIDAD
NO EXISTE IRREGULARIDAD
615743.44
ࡷ࢏
࢑ ࢏ା૚
൏
૙ Ǥ
૟
Se tiene irregularidad extrema de rigidez, por lo que se trabaja
con un Ia = 0.50
Rigidez primer piso Rigidez segundo y tercer piso

13. IRREGULARIDADES DE ALTURA
IRREGULARIDADES DE MASA O PESO
No se tiene irregularidad de masa
PISO
1
2
3 130.50
1
1.17
153.00 NO EXISTE IRREGULARIDAD
153.00 NO EXISTE IRREGULARIDAD
PESO (Wi) OBSERVACION
ࢃ࢏
ࢃ࢏ା૚
൐ ૚ Ǥ
૞

14. IRREGULARIDADES DE ALTURA
IRREGULARIDADES DE GEOMETRIA VERTICAL
No se tiene irregularidad de geometría vertical
PISO
1
2
3
12.00
12.00
EL EDIFICIO ES REGULAR Y CONSTANTE
EN TODOS SUS PISOS
NO EXISTE
IRREGULARIDAD
b (ancho de piso )m OBSERVACION
12.00
࢈૛
࢈૚
൐ ૚ Ǥ
3

15. IRREGULARIDADES DE ALTURA
OTRAS IRREGULARIDADES
No se tiene irregularidad de discontinuidad
IRREGULARIDAD OBSERVACION
DISCONTINUIDAD EN LOS SISTEMAS RESISTENTES
COMO TODA LA ESTRUCTURA ES REGULAR Y DE
SECCIONES CONSTANTES EN TODO LOS PISOS NO
CALIFICA COMO DISCONTINUIDAD EN LOS SISTEMAS

16. IRREGULARIDADES DE PLANTA
IRREGULARIDADES EN GENERAL
Se trabaja con un Ip = 1
DISCONTINUIDAD DEL DIAFRAGMA
LA ESTRUCTURA TIENE CONTINUIDAD DE DIAFRAGMA
HASTA EL ULTIMO PISO
ESQUINAS ENTRANTES
NO TENEMOS LOS DATOS SUFICIENTES PARA PODER
DEFINIR IRREGULARIDAD TORSIONAL
LA ESTRUCTURA NO POSEE ESQUINAS ENTRANTES
TORSIONAL
IRREGULARIDAD OBSERVACION

17. PASO 4: Cálculo del COEFICIENTE DE REDUCCIÓN DE LAS FUERZAS SÍSMICAS “R”
Ro= 8
Ia = 0.5
Ip = 1
R= 8x0.5x1
R=4

18. PASO 5: Cálculo del FACTOR DE USO “U” A
U = 1

19. PASO 6: Cálculo del PESO SÍSMICO (P)
PISO CM(Ton/m2) CV (Ton/m2) AREA (m2) FACTOR CV Pi (Ton)
1 0.8 0.2 180 0.25 153
2 0.8 0.2 180 0.25 153
3 0.7 0.1 180 0.25 130.5
PESO SISMICO (100%CM + …..%CV)
436.5 Tn
PESO SISMICO (P)

20. PASO 7: CÁLCULO DE LA CORTANTE BASAL
El valor de
C 2.50
R 4
C/R 0.625 CORRECTO

21. PASO 8: DISTRIBUCIÓN DE FUERZA SÍSMICA EN ALTURA
(4.5.3 N-E030)

22. Para comprobar si está bien hecha nuestra
distribución de fuerzas sísmicas en altura,
realizamos lo siguiente:
𝐹1+ 𝐹2+𝐹3=𝑉
25.26+48.53+61.24=135.04… 𝑂𝐾
𝛼=
𝑃𝑖 ∗h𝑖𝑘
∑ 𝑃𝑖 ∗h𝑖𝑘

23. B) Calcule los desplazamientos elásticos e inelásticos de los 3 niveles ,
en función del lado de las columnas “c”
PASO 01: CALCULAR LA RIGIDEZ DE ENTREPISO
DATOS:
E 2200000 Ton/m2
N° ELEMENTOS 12
Rigidez primer piso
Rigidez segundo y tercer piso

24. K1
K2
K3
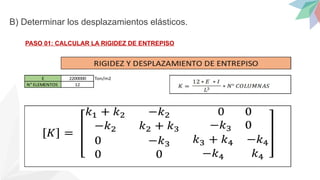
Reemplazamos datos en la siguiente matriz:
PASO 02: CALCULAMOS LOS DESPLAZAMIENTOS DE ENTREPISO
[ 𝐷 ]=[ 𝐾 ]−1
∗[ 𝐹𝑖 ]

25. • Reemplazamos nuestra matriz de fuerzas, con las fuerzas de
distribución sísmica calculadas en el paso 8
• Calculamos la inversa la matriz K

26. PASO 3: CÁLCULO DE DERIVAS
Deriva

27. C) Calcule el tamaño de la columna para que las derivas del edificio no
sobrepase los valores máximos definidos en la norma.
ALTURA DE
ENTREPISO
(m)
PISO
3.8 1
3.5 2
3.5 3
0.00030 0.001005 0.007 0.6155
0.00005
DERIVA ELASTICA DERIVA INELASTICA
DERIVA MAXIMA
(CONCRETO)
0.00003 0.000097 0.007 0.3428
0.000173 0.007 0.3966
Cൌ
ாோூ ூோ
ௌ்ூ
ாோூ ெ
ூெ
ర
‫ܣ‬ ܸ
‫ܫ‬ ܴ
‫ܦܧ‬
‫ܥ‬ସ
‫ܣ‬ ܸ
‫ܫ‬ ܴ
‫ܦܧ‬
‫ܥ‬ସ
‫כ‬ ͲǤ
ͺͷ‫כ‬ ܴ
OBSERVACION DE C
EL VALOR DE C SERA MAYOR DE 0.62m ,
PARA QUE LAS DERIVAS NO
SOBREPASEN LOS VALORES MAXIMOS
COLUMNA
C X C
0.65m * 0 .65m
REEMPLAZODEC=0.65ENLA DERIVA
INELASTICA
0.0056
0.0005
0.0010
‫ܣ‬ ܸ
‫ܫ‬ ܴ‫ܦܧ‬
‫ܥ‬ସ
‫כ‬ͲǤ
ͺͷ‫כ‬ܴ

28. D) Partiendo de las fuerzas halladas en (A), calcule el periodo
fundamental en X-X empleando la expresión de Rayleigh. Con este
nuevo periodo ¿Cambiará la fuerza cortante basal?

29. PISO DESPLAZAMIENTO Pi g fi Pi*di^2 fi*di
1 0.0011227 153 25.26 0.00019286 0.02836
2 0.0013010 153 48.53 0.00025898 0.06314
3 0.0014005 130.5 61.24 0.00025596 0.08577
T 0.12676
T
T 0.3000
9.81
0.000707792 0.177280
෍ ܽ ݅
‫ݎ‬ ܽ ݉ ‫ݏ‬
‫ݐ‬ ‫ݑ‬
ͳ
‫ܥ‬ଶ
ͲǤ
ͳʹ
‫ܥ‬ଶ
ൌ
ͲǤ
ͳʹ
ͲǤ
ͷ ଶ
PERIODO FUNDAMENTAL (EXPRESION DE RAYLEIGH)

30. VERIFICACIÓN
• DATOS ANTERIORES • DATOS NUEVOS
PERFIL S3
T(p) 1
T(L) 1.6
Hn 10.8
CT 35
T
0.309
C 2.50
PERFIL S3
T(p) 1
T(L) 1.6
T 0.300
C
2.50
El PERIODO DISMINUYE EN 0.009 CON UNA
DIMENSION DE COLUMNA DE 0.65 X 0.65 , SI
SE AUMENTARA LAS DIMENSIONES DE
COLUMNA DISMINUIRIA EL PERIODO DE
RAYLEIGH
OBSERVACION

31. PERFIL S3 PERFIL S3
T(p) 1 T(p) 1
T(L) 1.6 T(L) 1.6
Hn 10.8 T 0.300
CT 35
T
0.309
C
2.50
C 2.50
Z 0.45
U 1
C 2.50 V 135.04 Tn
S 1.1
R 4
P 436.5
El PERIODO DISMINUYE EN 0.009 CON UNA
DIMENSION DE COLUMNA DE 0.65 X 0.65 , SI
SE AUMENTARA LAS DIMENSIONES DE
COLUMNA DISMINUIRIA EL PERIODO DE
RAYLEIGH
CONCLUSION
LA CONSTANTE DE AMPLIFICACION SISMICA
ES DEPENDIENTE DEL PERIODO. SIN
EMBARGO, NO VARIA CON EL NUEVO
PERIODO POR LO QUE LA CORTANTE BASAL
PERMANECE CONSTANTE
VERIFICACION DE CORTANTE BASAL
OBSERVACION
ܸ ൌ
ܼ ‫כ‬ ܷ ‫ܥכ‬ ‫כ‬ ܵ
ܴ
‫כ‬ ܲ

32. EJERCICIO 02
La figura muestra un edificio irregular de oficina que se construirá en Trujillo sobre un suelo S2.
Se hará un análisis preliminar en la dirección X-X usando el método traslacional de corte y las
fuerzas del método estático de la NTE-030-2018.
A) Determine la fuerza cortante en la base y la distribución de las fuerzas en altura. Estime el
periodo con la expresión T=hn/Ct.
B) Determinar los desplazamientos elásticos.
C) Determine los desplazamientos laterales máximos esperados según NTE-030 e indique si estos
satisfacen los requisitos de rigidez.
D) En caso de rigidizar el edificio, determine el lado mínimo de las columnas cuadradas (múltiplo de
5cm) para lograrlo. Con estos nuevos valores, recalcule el sistema de fuerzas y los
desplazamientos.

33. • Dibuje el diagrama de fuerzas cortantes y momento flector para una
columna de 4 pisos.
• DATOS: Carga total (Muerta+Viva reducida)
Pisos 1 a 3 = 1ton/m2,
piso 4: 0.9 ton/m2

34. MODELADO DEL PORTICO 3D

35. DATOS GENERALES
- N° de columnas por 1,2,3 piso : 12 COLUMNAS
- N° de columnas por 4 piso : 9 COLUMNAS
- E = 2200000 Ton/m2
- Dimensiones de la columna cuadrada : C X C
- Rigidez de columnas empotradas
- Inercia de columna

36. PASO 01: VERIFICAMOS IRREGULARIDADES EN ALTURA Y EN PLANTA
• Para ello, primero
hallamos la
rigidez de cada
entrepiso
ENTREPISO E(Ton/m2) altura(m) I=b*d^3/!2N° (columnas) Kentrepiso
1 E 3.4 I 12 12.46EI
2 E 2.8 I 12 18.37EI
3 E 2.8 I 12 18.37EI
4 E 2.8 I 12 18.37EI
RIGIDEZ DE ENTREPISO
A) Determinar la fuerza cortante en la base y la distribución
de las fuerzas. Estime el periodo con la expresión .

37. IRREGULARIDADES DE ALTURA
IRREGULARIDADES EXTREMA DE RIGIDEZ
Se tiene irregularidad extrema de rigidez, por lo que se trabaja
con un Ia = 0.50
Rigidez en todos lo pisos

38. IRREGULARIDADES DE ALTURA
IRREGULARIDADES DE MASA O PESO
Se tiene irregularidad de masa, es decir, un Ia = 0.9
PISO Pi (Ton)
1 226.8
2 226.8
3 226.8
4 136.08
100%CM+ …%CV
1.00
AREA (m2)
226.80
226.80
226.80
151.20
1.00
1.00
0.90

39. IRREGULARIDADES DE ALTURA
IRREGULARIDADES DE GEOMETRIA VERTICAL
Esta irregularidad tiene un valor mayor comparado con la
irregularidad de rigidez extrema, por lo que se escoge el
menor Ia = 0,50
PISO Largo h(m)
1 18.9
2 18.9
3 18.9
4 12.6
OBSERVACION
b (ancho de piso )m
12.00
12.00
12.00
12.00
EN UN SENTIDO EXISTE REGURALIDAD , EN OTRO NO
࢈૛
࢈૚
൐ ૚ Ǥ
3

40. IRREGULARIDADES DE PLANTA
IRREGULARIDADES EN GENERAL
Se trabaja con un Ip = 1

41. IRREGULARIDADES ESTRUCTURALES EN ALTURA
El edificio presenta irregularidad en altura , por lo tanto:
PASO 02: CÁLCULO DE LA CORTANTE BASAL
Para calcular el cortante basal de la estructura, debemos conocer los siguientes factores:
Z= factor de zona
U= factor de uso
C= factor de amplificación sísmica
S= factor de suelo
R= coeficiente de reducción de las fuerzas sísmicas
P= peso sísmico

42. Según el problema la vivienda se construirá en la ciudad de
Trujillo sobre suelo S2.
Nos dirigimos a la Norma E-030, para poder tomar los valores
correspondientes
Z=0.45
S=1.05

43. 2.1. Cálculo del factor “C”

44. • Hallaremos , ya que estos datos nos servirán para
encontrar el factor de amplificación sísmica (C)
=0.6
=2

45. • Hallaremos
Hn 11.8
CT 35
T 0.337

46. • Después de haber calculado Tp, TL, y T, vamos a definir el
factor de amplificación sísmica.
• =0.6
• =2
• T =0.337
T<Tp
0.337<0.6, C=2.5

47. Cálculo del COEFICIENTE DE REDUCCIÓN DE LAS FUERZAS SÍSMICAS “R”
Ro= 8
Ia = 0.5
Ip = 1
R= 8x0.5x1
R=4

48. Cálculo del FACTOR DE USO “U” A
U = 1

49. Cálculo del PESO SÍSMICO (P)

50. CÁLCULO DE LA CORTANTE BASAL
El valor de
C 2.50
R 4
C/R 0.625 CORRECTO

51. DISTRIBUCIÓN DE FUERZA SÍSMICA EN ALTURA
(4.5.3 N-E030)

52. Para comprobar si está bien hecha
nuestra
distribución de fuerzas sísmicas en altura,
realizamos lo siguiente:
𝐹1+ 𝐹2+𝐹3=𝑉
31.92+58.21+84.50+66.48=241.12…𝑂𝐾
𝛼=
𝑃𝑖 ∗h𝑖𝑘
∑ 𝑃𝑖 ∗h𝑖𝑘

53. B) Determinar los desplazamientos elásticos.
PASO 01: CALCULAR LA RIGIDEZ DE ENTREPISO

54. K1
K2
K3
K4
Reemplazamos datos en la siguiente matriz:
PASO 02: CALCULAMOS LOS DESPLAZAMIENTOS DE ENTREPISO
[ 𝐷 ]=[ 𝐾 ]−1
∗[ 𝐹𝑖 ]

55. • Reemplazamos nuestra matriz de fuerzas, con las fuerzas de
distribución sísmica calculadas anteriormente
• Calculamos la inversa la matriz K

57. C) Determine los desplazamientos laterales máximos esperados según
NTE-030 e indique si estos satisfacen los requisitos de rigidez

59. Desplazamientos laterales máximos
Reemplazo de C = 0. 5m
0.0048820 PISO 1
[Dlat] = 0.0072477 PISO 2
0.0089551 PISO 3
0.0099574 PISO 4

ܽ ݈‫ܦ‬
‫ݐ‬ ൌ
ͲǤ
ͺͷ‫כ‬ ‫ܦ‬ /C^4

60. D) En caso de rigidizar el edificio, determine el lado mínimo de las
columnas cuadradas (múltiplo de 5cm) para lograrlo. Con estos nuevos
valores, recalcule el sistema de fuerzas y los desplazamientos.
PERIODO FUNDAMENTAL (EXPRESION DE RAYLEIGH)
PISO DESPLAZAMIENTO Pi g fi Pi*di^2 fi*di
1 0.0003590 226.8 31.92 0.00002923 0.01146
2 0.0005329 226.8 58.21 0.00006441 0.03102
3 0.0006585 226.8 84.50 0.00009833 0.05564
4 0.0007322 136.08 66.48 0.00007295 0.04867
0.000191971 0.098125
T 0.08873
T
T 0.246
9.81
෍ ܽ ݅
‫ݎ‬ ܽ ݉ ‫ݏ‬
‫ݐ‬ ‫ݑ‬
ͳ
‫ܥ‬ଶ
ͲǤ
Ͳͺͺ͵
‫ܥ‬ଶ ൌ
ͲǤ
Ͳͺͺ͵
ͲǤ
ͷଶ

61. PERFIL S3 PERFIL S3
T(p) 1 T(p) 1
T(L) 1.6 T(L) 1.6
Hn 10.8 T 0.246
CT 35
T
0.309
C
2.50
C 2.50
Z 0.45
U 1
C 2.50 V 241.12 Tn
S 1.05
R 4
P 816.48
El PERIODO DISMINUYE EN 0.063 CON UNA
DIMENSION DE COLUMNA DE 0.5 X 0.5 , SI SE
AUMENTARA LAS DIMENSIONES DE
COLUMNA DISMINUIRIA EL PERIODO DE
RAYLEIGH
CONCLUSION
LA CONSTANTE DE AMPLIFICACION SISMICA
ES DEPENDIENTE DEL PERIODO. SIN
EMBARGO, NO VARIA CON EL NUEVO
PERIODO POR LO QUE LA CORTANTE BASAL
PERMANECE CONSTANTE
VERIFICACION DE CORTANTE BASAL
OBSERVACION
ܸ ൌ
ܼ ‫כ‬ ܷ ‫ܥכ‬ ‫כ‬ ܵ
ܴ
‫כ‬ ܲ

64. Distribución de cortante y momentos en columna
Eje – A EXTERIOR

67. FUERZAS
CORTANTES Y
MOMENTOS
FLECTORES