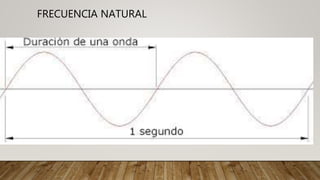
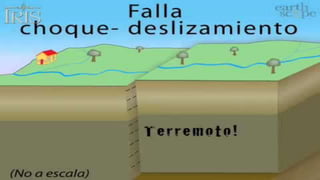
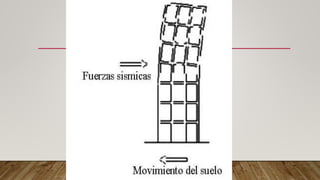
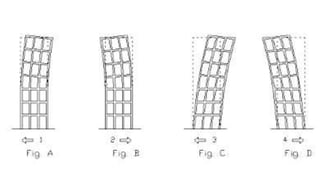
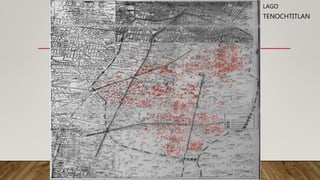
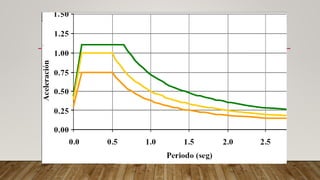
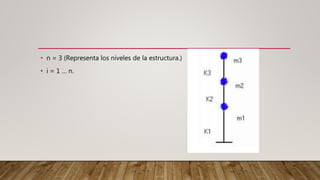
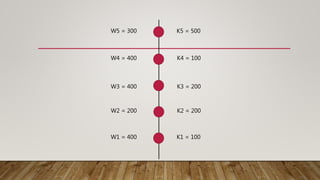
El documento explica los conceptos de resonancia y cómo afecta el comportamiento sísmico de las estructuras. La resonancia ocurre cuando la frecuencia de una fuerza externa coincide con la frecuencia natural de un objeto, haciendo que oscile con mayor amplitud. El terremoto de la Ciudad de México de 1985 causó daños extensos debido a la resonancia producida por los suelos blandos debajo de los edificios. El documento también presenta un modelo matemático para calcular los períodos fundamentales de vibración de las estructuras.

1. RESONANCIA
FABIÁN CASTRO NÚÑEZ

2. OBJETIVO:
• El objetivo de este trabajo es darle al lector una visión más amplia
sobre los efectos de la resonancia en las estructuras y explicar las
causas, para así poder desarrollar nuevos métodos y modelos
matemáticos que ayuden al diseño, tomando en cuenta el
comportamiento sísmico de la estructura.

3. RESONANCIA
• Cuando dos eventos están sincronizados a una
misma frecuencia, se entra en un estado de
resonancia.

4. La energía no se crea ni se destruye, solo se
transforma. (Antoine Lavoisier)
ENERGÍA

8. FRECUENCIA NATURAL

10. FUERZA EXTERNA

11. DESARROLLO DEL TEMA:
• Cuando la frecuencia producida por una acción es de la misma
magnitud que la frecuencia natural del objeto receptor, se llega
a una condición de resonancia. Ésta es la que permite que el
objeto tienda a oscilar con una amplitud mayor en algunas
frecuencias.

12. • VIDEO
• https://www.youtube.com/watch?v=EzdjlNu2CWM

13. MOVIMIENTOS TECTÓNICOS
• Movimientos bruscos provenientes de la corteza terrestre,
las cuales producen una liberación de energía, traducidas
en ondas sísmicas

15. ENERGÍA SÍSMICA:
• Energía: Capacidad física de generar trabajo.
• Los sismos generan energía, que es transmitida a la superficie.

16. • Genera movimiento de la estructura que se frena por la
resistencia interna, transformando la energía cinética en
energía potencial, causando deformaciones que provocan
las oscilaciones conocidas en la estructura.

20. RESONANCIA EN ESTRUCTURAS:
• Aumento en amplitud en el movimiento de un sistema, el
cual está siendo sometido a una fuerza que esta
sincronizada con el movimiento de dicho sistema

21. • Los sismos pueden producir Energía que llega a
recorrer gran parte de la tierra, que alcanza a
ciudades por el efecto de ondas sísmicas. Estas
pueden viajar por la superficie del terreno o en
profundidades.

22. SISMO EN LA CIUDAD DE MÉXICO

24. • Jorge Flores Valdés, investigador del IFUNAM (Instituto de
Física de la UNAM), dedicado desde hace más de 25 años
al estudio de los sismos, vivió el suceso como ciudadano y
también como científico.

25. • “Cayeron casi 500 edificios, la mayoría entre 7 y 12 pisos
de altura y construidos de manera similar. Pero lo más
interesante es que todos los edificios que se colapsaron,
sin excepción, estaban construidos sobre lo que era el
antiguo lago de Tenochtitlan”, explica.

26. • Y continúa: “En las partes de montañas que rodean al lago
o de terrenos más o menos duros no se cayó nada. Casi ni
se rompieron los vidrios”.

27. LAGO
TENOCHTITLAN

28. • “Cuando un físico ve el mapa de daños como este,
la conclusión es clara: es una función de onda
atrapada en el lago y es una resonancia” (Jorge
Flores Valdés).

29. • Zonas de sedimentos y rocas.
• Hubo un aumento en la amplitud del movimiento sísmico
debido a un movimiento colectivo de las arcillas del
subsuelo.

30. • Al pasar de un terreno duro a uno suave bruscamente
ocurre una transferencia de energía de las ondas sísmicas
entrantes a ondas longitudinales, lo cual hace que éstas
amplíen su movimiento.

31. • VIDEO
• https://www.youtube.com/watch?v=kn4GAbyrjps

32. • Cuando hablamos de frecuencia, si la frecuencia de la estructura es
mayor que la frecuencia del suelo, la energía sísmica disminuye,
logrando reducir daños importantes a dicha estructura.
• Mientras dicha diferencia sea más grande menos peligro habrá en la
estructura ya que no habría un acoplamiento de frecuencias.

33. EFECTOS DE INTERACCION SUELO-ESTRUCTURA
• Las estructuras con una planta baja flexible son
vulnerables a los sismos por la falta de rigidez y resistencia
en el piso blando.
• Para asegurar un correcto funcionamiento habrá que
diseñar y mantener regularidad con el sistema estructural
tanto en la planta baja, como en las plantas posteriores.

34. • Es importante conocer esta interacción debido a que los
tipos de suelos que hay no siempre serán los más
adecuados, existen los suelos blandos, así como las
arcillas.
• También el tipo de cimentación utilizada puede ser
afectada por dicha interacción

36. • Donde se sigue la norma contra sismos, bajo una
supervisión estricta, el daño es mucho menor.

37. CONSIDERACIONES
• Clasificación de las estructuras
• Espectros de sitio y regionalización, espectros de acelerogramas.
• Factores de reducción
• Análisis

39. PREVENCIONES
• Diseñar en base a la respuesta del suelo en la region.
• Añadir tipos de aisladores en la base de la estructura.
• Añadir amortiguadores para reducir la respuesta al sismo.

41. • Con lo ya antes mencionado se tendrán ahora que
presentar la forma de calcular con mayor precisión los
periodos fundamentales de vibración de estructuras, con
ayuda de modelos matemáticos.

42. • A lo largo de los años, se han realizado diferentes estudios, y se han
desarrollado diferentes modelos realizados por diversos
investigadores y estos muchas veces son de tipo analíticos o
empíricos.

43. • El estudio que a continuación se mostrará es un modelo
de tipo analítico desarrollado por la:
Sociedad Mexicana de Ingeniería Estructural, A.C.,
Ingeniero José Alejandro Gómez Hernández.

45. • Se comparó con otros modelos aceptados
internacionalmente, así como lo es el método de
Newmark, cociente de Schwartz, entre otros.

46. El modelo está fundamentado en base a:
• El comportamiento de una estructura de tipo elástico
lineal.
• Modelo unidimensional

47. • n = 3 (Representa los niveles de la estructura.)
• i = 1 … n.

48. VARIABLES Y PARAMETROS
• 𝑢𝑖 = 𝑉∗ 1
𝑖 1
𝑘 𝑖
• Desplazamiento total por cortante en el sentido “x”. Donde la V = Fuerza
cortante
• 𝜆 =
6−(
1
𝑛
) 𝑛−1
5
• Factor Lambda en función del número de niveles.

49. • 𝐾𝑖 =
𝑉
𝑈 𝑖−𝑈 𝑖−1
• Rigidez de entrepiso cortante.
• G = 9.81 m/seg2
• Aceleración de la gravedad.

50. • 𝑊𝑖 = 𝑚𝑖 ∗ G
• Peso del nivel “i”.
• 𝑋𝑖 =
1
𝑖 1
𝐾 𝑖
1
𝑛 1
𝐾 𝑖
• Componentes del vector del primer modo, aproximación
estática.

51. • Periodo fundamental de vibración de nuestra estructura:
• 𝑇𝑒 =
2𝜋𝜆
𝐺
∗ 1
𝑛 1
𝐾 𝑖
∗ 1
𝑛
𝑊𝑖 ∗ 𝑋𝑖
2

52. • El uso de este modelo considera los efectos de
amplificación o atenuación dinámica y podemos
considerar dicho modelo como casi exacto.
• Las diferencias entre resultados son menores al 10%
comparándolo con otros modelos.

53. MODELO DE NEWMARK
• El modelo de Newmark está basado en una teoría de
elasticidad lineal, el cual determina el periodo
fundamental de vibración en un sistema de masas
continuas.

54. MODELO DEL SMIE
• Determina el incremento o la disminución de los
desplazamientos y esfuerzos actuantes, en base al cambio
de rigideces y masas entre niveles.

55. EJEMPLO
• Datos:
• n = 5, i = 1, G = 9.81 m/s^2
• Peso en Ton:
• W1= 400 W2 = 400 W3 = 400 W4 = 400 W5 = 300
• Rigideces en Ton/cm:
• K1 = 100 K2 = 200 K3 = 200 K4 = 100 K5 = 100

56. W4 = 400
W3 = 400
W2 = 200
W1 = 400
W5 = 300 K5 = 500
K4 = 100
K1 = 100
K2 = 200
K3 = 200

57. • 𝑋𝑖 =
1
𝑖 1
𝐾 𝑖
1
𝑛 1
𝐾 𝑖 i Xi (Xi)2
1 0.25 0.063
2 0.375 0.141
3 0.5 0.25
4 0.75 0.563
5 1 1

58. X4 = 0.75
X3 = 0.50
X2 = 0.375
X1 = 0.25
X5 = 1.00

59. • Peso Total de los n Niveles:
• 𝑊𝑇 = 𝑖=1
𝑛
𝑊𝑖
• 𝑊𝑇 = 1.9𝑥10^3

60. • Factor Lambda
• 𝜆 =
6−(
1
𝑛
) 𝑁−1
5
• 𝜆 = 1.095

61. • 𝑇𝑒 =
2𝜋𝜆
𝑔
∗ 1=1
𝑛 1
𝐾 𝑖
∗ 1=1
𝑛
𝑊𝑖 ∗ 𝑋𝑖
2
• Te = 1.168 seg.
• Por el cálculo del cociente de Schwartz,de la fuente: “Diseño Sísmico de edificios –
Editorial LIMUSA – 1998” del Cr. R. Meli y el Dr. E.
• Te = 1.17 seg.

62. CONCLUSIONES
• Todo modelo que en la actualidad existe para un cálculo
en particular fue en su tiempo a partir de hipótesis y los
cuales, a través de la aplicación y por fundamentación
teórica, fueron tomando forma hasta llegar a los modelos
que ahora conocemos

63. • También podemos obtener modelos matemáticos
deducidos en base a hipótesis que formulan métodos más
simplificados como es el caso del modelo aquí
presentado.

64. • Es muy importante tener en cuenta el periodo
fundamental del suelo y la estructura, ya que de
ahí se basará el comportamiento dinámico de la
misma estructura.

65. GRACIAS POR SU ATENCION