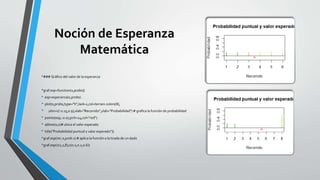
Este documento presenta una serie de aplicaciones del análisis matemático y la probabilidad y estadística utilizando Python y R. Incluye ejemplos de gráficas de funciones, sumas, integración numérica, simulaciones probabilísticas y gráficos estadísticos comunes. El documento proporciona código de Python y R con comentarios para ilustrar diferentes métodos.

1. Prof Débora Chan
Aplicaciones de Análisis Matemático I y II
Probabilidad y Estadística
Python-R

2. Análisis Matemático
Phyton y R

3. Aplicaciones de
Análisis Matemático I
y II (Python-R)
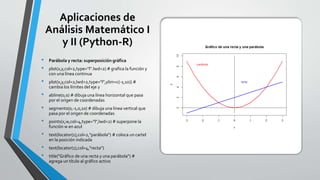
Graficación de Haz de rectas
• m=seq(-50,50,5) # define las distintas pendientes
• x=seq(-1,1,0.1) # asigna valores a x
• y=x*(m[1]) # devuelve los valores de y en función de x
• plot(x,y,type="l",ylim=c(-4,4)) # grafica la primera recta
• for (i in 2:length(m)){ y=x*m[i]
• points(x,y,type="l",col=i)} # grafica el haz de rectas
• abline(v=0) # grafica la recta vertical
• title("Haz de rectas por el origen de coordenadas")

4. Aplicaciones de
Análisis Matemático I
y II (Python-R)
• Parábola y recta: superposición gráfica
• plot(x,y,col=2,type="l“.lwd=2) # grafica la función y
con una línea continua
• plot(x,y,col=2,lwd=2,type="l",ylim=c(-1,10)) #
cambia los límites del eje y
• abline(0,0) # dibuja una línea horizontal que pasa
por el origen de coordenadas
• segments(0,-1,0,10) # dibuja una línea vertical que
pasa por el origen de coordenadas
• points(x,w,col=4,type="l",lwd=2) # superpone la
función w en azul
• text(locator(1),col=2,"parábola") # coloca un cartel
en la posición indicada
• text(locator(1),col=4,"recta")
• title("Gráfico de una recta y una parábola") #
agrega un título al gráfico activo

5. Efecto de la fase en la
graficación de funciones
trigonométricas
• x=seq(-5,5,.1)
• y=sin(x) # define una curva senoidal
• w=sin(x+pi/3) # define una curva senoidal con el mismo período pero
distinta fase
• z=sin(x-pi/4)
• plot(x,y,type="l",col="brown",axes=F) # grafica la función y sin los ejes
• plot(x,y,type="l",lwd=2.5,col="brown",axes=T) # grafica la función y con
los ejes
• plot(x,y,type="l",lwd=2.5,col="brown",axes=T,xlab="eje x",ylab="eje y")
# pone nombre a los ejes
• plot(x,y,type="l",lwd=2.5,col="brown",axes=T,xlab="eje x",ylab="eje
y",main="Senoidales con diferentes fases")
points(x,w,type="l",lwd=2.5,col="green") # superpone la función w
• points(x,z,type="l",lwd=2.5,col="violet") #superpone la función z
• a=expression(paste(alpha,"=",0)) # escribe letras griegas
• b=expression(paste(alpha,"=",pi/3)); c=expression(paste(alpha,"=",-pi/4))
• legend.text=c(a,b,c)
• legend("topright",legend.text,text.col=c("brown","green","violet"),cex=0
.9,text.width=0.8) # coloca una leyenda

6. Aplicaciones de
Análisis Matemático I
y II (Python-R)
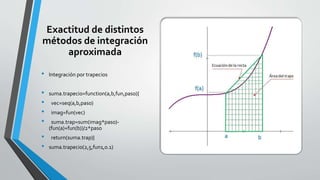
• Sumas Inferiores
• ###Sumas Inferiores
• minimo=0
• suma.inf=function(a,b,fun,paso){
• vec=seq(a,b,paso)
• n=length(vec)-1
• for (i in 1:n){
minimo[i]=min(fun(seq(vec[i],vec[i+1],paso))) }
• suma.inf=sum(minimo*paso)
• return(suma.inf)}

7. Aplicaciones de
Análisis Matemático I
y II (Python-R)
• Sumas Superiores
• maximo=0
• suma.sup=function(a,b,fun,paso){
• vec=seq(a,b,paso)
• n=length(vec)-1
• for (i in 1:n){
• maximo[i]=max(fun(seq(vec[i],vec[i+1],paso))) }
• suma.sup=sum(maximo*paso)
• return(suma.sup)}

8. Exactitud de distintos
métodos de integración
aproximada
• Integración por trapecios
• suma.trapecio=function(a,b,fun,paso){
• vec=seq(a,b,paso)
• imag=fun(vec)
• suma.trap=sum(imag*paso)-
(fun(a)+fun(b))/2*paso
• return(suma.trap)}
• suma.trapecio(2,5,fun1,0.1)

9. Integración Ley de
los Grandes
Números
•suma.lgn=function(a,b,fun,n){
• vec=runif(n,a,b)
• imag=fun(vec)
• suma.lgn=mean(imag)*(b-a)
• return(suma.lgn)}
•suma.lgn(2,5,fun1,1000)

10. Integrales con
herramientas de R
• Integrales de funciones triangulares
•### Distribución triangular simétrica
• triang=function(x){
• if (x<0|x>2) {triang=0}
• else if (x>=0 & x<1) {triang=x}
• else {triang=2-x}
• return(triang)}
• ej1=seq(-1,3,0.1)
• ej2=Vectorize(triang)(ej1) # vectoriza una función escalar
• plot(ej1,ej2,type="l",col="purple",lwd=2,main="Distribución
triangular simétrica",xlab="x",ylab="f(x)")
• abline(0,0)

11. Graficación de
planos con
Python

12. Aplicaciones de
Análisis Matemático I y
II (Python-R)
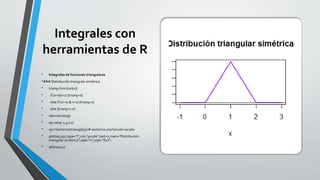
• Recta tangente a la lemniscata de Bernoulli
• alfa=seq(0,2*pi,0.01) # asigna valores al parámetro
• x=cos(alfa)/(1+sin(alfa)**2) # define la variable x en función del parámetro
• y=cos(alfa)*sin(alfa)/(1+sin(alfa)**2)# define la variable y en función del parámetro
• par(bg = "papayawhip") # establece el color del fondo
• plot(x,y,lwd=2,type="l",col="royalblue1") # grafica la curva
• abline(0,0) ;segments(0,-1,0,1)
• rtx=seq(-1,1,0.1)*(x[472]-x[471])/0.01+x[471] # calcula una aproximación de la
derivada cerca del origen
• rty=seq(-1,1,0.1)*(y[472]-y[471])/0.01+y[471]
• points(rtx,rty,col="seagreen",type="l",lwd=2) # superpone la recta tangente
• title("Lemniscata de Bernoulli")

13. Aplicaciones de
Análisis Matemático I y
II (Python-R)
• Superficies en el espacio: distribución normal
bivariada

14. Aplicaciones de
Análisis Matemático I y
II (Python-R)
• Superficies en el espacio: paraboloide elíptico
• par(bg="papayawhip")
• fun1=function(x,y) {x^2 + y^2} # define un paraboloide circular
• fun2=function(x,y) exp(-x^2 - y^2) # definie la función de la
distribución normal bivariada con ro=0
• fun3=function(x,y) x+y # define un plano
• x=seq(-3,3,0.1)
• y=x
• persp(x,y,outer(x,y,fun1), col="tomato3") # grafica la función fun1
paraboloide

15. Curvas de nivel
•x=y=seq(-4*pi,4*pi,len=27)
•r=sqrt(outer(x^2,y^2,"+"))
•filled.contour(exp(-
0.1*r),axes=FALSE) # grafica las curvas
de nivel

16. Aplicaciones de
Análisis Matemático I
y II (Python-R)
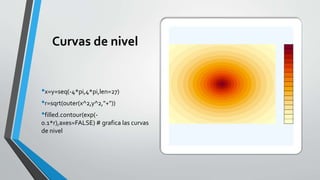
• Curva definida en forma paramétrica
• plt.rcParams['legend.fontsize'] = 10
• fig = plt.figure()
• ax = fig.gca(projection='3d')
• # x, y, z
• theta = np.linspace(-4 * np.pi, 4 * np.pi, 100)
• z = np.linspace(0, 2, 100)
• r = z**2 + 1
• x = r * np.sin(theta)
• y = r * np.cos(theta)
• ax.set_title('Curva Paramétrica');
• ax.plot(x, y, z)
• ax.legend()
• ax.scatter([0], [0.7], [0], color="g", s=100)
• ax.scatter([0], [1.2], [0.5], color="r", s=100)
• ax.scatter([1], [2], [1], color="y", s=100)
• ax.scatter([1.8], [3], [1.5], color="b", s=100)
• plt.show()

17. PlanoTangente a una
Superficie en el Espacio

18. Probabilidad y
Estadística

19. Gráficos estadísticos:
Diagrama Circular
•pie3D(frec.catpeso,labels=etiquetas,explode=0
.1,
•labelcex=0.9,radius=1.5,height=0.2)
•# cambia el alto de la torta
•pie3D(frec.catpeso,labels=etiquetas,explode=0
.1,
•labelcex=0.9,radius=1.5,height=0.2,shade=0.6)

20. Gráficos Estadísticos:
Diagrama de barras
•p1=ggplot(IMCinfantil,aes(x=CatPeso))+geom_bar(aes(fill
=SEXO))# barras superpuestas por sexo
•p1
• p2=ggplot(IMCinfantil,aes(x=CatPeso))+
• geom_bar( aes(x=CatPeso,fill =
SEXO),position=position_dodge()) #barras adyacentes
•p2

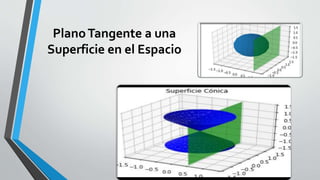
21. Gráficos Estadísticos:
Mosaicos
•tabla2=table(EDAD,CatPeso)
•mosaicplot(tabla2) # hace un gráfico de
mosaicos simple
•
mosaicplot(tabla2[,c(1,2,4,3)],col=c("cadetblue1
","deepskyblue","deepskyblue4","cyan3"),main=
"Gráfico de Mosaicos",ylab="Categoría de
Peso",xlab="Edad", cex=0.8) # este gráfico
permite visualizar una tabla de contingencia

22. Gráficos
Estadísticos:
Diagrama de
dispersión
grupo=factor(avispas$Grupo)
plot2=ggplot(avispas, aes(x =X1, y = X2,col=grupo)) +
geom_point()
plot2

23. Gráficos Estadísticos:
Histogramas Polígonos
de Frecuencias
•plot1=ggplot(IMCinfantil,aes(x=PESO))+geom_histo
gram(binwidth =
8,color="aquamarine3",fill="cadetblue",alpha=0.2)
•plot1
•sexo=factor(IMCinfantil$SEXO)
•plot2=ggplot(IMCinfantil,aes(x=TALLA,fill=sexo))+
•geom_density()
•plot2

24. Gráficos
estadísticos: Curvas
de Densidad
• plot8=ggplot(IMCinfantil,aes(x=TAL
LA,fill=sexo))+
• geom_density()
• plot8

25. Gráficos Estadísticos:
Boxplot
•plot13=ggplot(IMCinfantil,
•aes(x=SEXO,y=PESO,color=SEXO))+
•geom_boxplot()
•plot13 # con borde de color

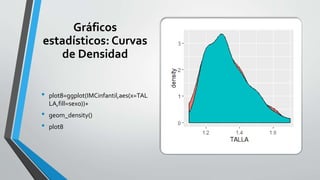
26. Gráficos
Estadísticos:
Caritas de
Chernov
•faces(galle.salad[,2:6],nco
l.plot=4) # acomoda la
cantidad de caras por fila

27. Gráficos Estadísticos:
correlogramas
•base.niños$CC=max(base.niños$CC)-base.niños$CC #
cambiamos una variable para que correlacione en forma
negativa con las restantes
•M=cor(base.niños) # calcula la matriz de correlación de
las variables de la base
•M
•corrplot(M,method="circle") # representa la matriz de
correlaciones mediante círculos

28. Simulaciones: La
moneda
•### Simulación de la tirada de una moneda
•exitos=0; tiradas=0; prob.est=0
•tiradas=rbinom(10000,1,0.5)
•for(i in 1:1000){
• exitos[i]=sum(tiradas[1:(i*10)])
• ensayos=seq(10,10000,10)
• prob.est[i]= exitos[i]/ensayos[i]}
•plot(ensayos,prob.est,type="l",col=3,
•lwd=1,main="Tendencia de la frecuencia relativa",
•xlab="Ensayos",ylab="Probabilidad estimada")
•abline(0.5,0,col=2,lwd=1)

29. Simulaciones: tiradas de
dado
• tiro.dado=0
• prob.est=0
• resultado=rep(0,6)
• dado=1:6
• simuladado=function(n){
• tiro.dado=sample(1:6,n,replace=TRUE)
• for(i in 1:6){
• resultado[i]=sum(tiro.dado==i)/n}
• return(barplot(resultado,lwd=4,col="gold",
• ylim=c(0,0.2),names.arg=1:6, main="Simulaci?n dado"))}
• simuladado(10000)

30. Simulaciones:Tiro
al Blanco-
Estimación de Pi
• n=100000; x1=runif(n,-1,1) ; x2=runif(n,-1,1); color=0
• for (i in 1:n){
• if (x1[i]^2+x2[i]^2<1/3) {color[i]="orchid2" }
• else if (x1[i]^2+x2[i]^2<1) {color[i]="chartreuse"}
• else {color[i]="cadetblue1"}}
• windows(width=6.5, height=6.5, rescale="fit")
• plot(x1,x2,col=color,xlab="",ylab="",main=paste("Tiro al blanco, n=",n), axes=F)
• prob.blanco=sum(color=="orchid2")/n
• prob.cerca=sum(color=="chartreuse")/n
• prob.fallo=sum(color=="cadetblue1")/n
• salida=list("Probabilidad de tiro al blanco"=prob.blanco,
• "Probabilidad de tiro cerca del blanco"=prob.cerca,
• "Probabilidad de tiro fallido"=prob.fallo)
• salida

31. Simulaciones:Tiro
al Blanco-
Estimación de Pi
• n=100000
• x1=runif(n,-1,1) # genera n datos con distribución uniforme en [-
1,1]
• x2=runif(n,-1,1)
• color=0 # inicializa la variable
• for (i in 1:n){
• if (x1[i]^2+x2[i]^2<1) color[i]="brown1"
• else color[i]="darkseagreen1"} # colorea según los puntos estén
dentro del círculo unitario o no
• windows(width=6.5,height=6.5,rescale="fit") # abre una ventana
con ciertas características
• plot(x1,x2,col=color) # grafica los puntos
• title(expression(paste("Aproximando ", pi)))

32. Noción de Esperanza
Matemática
•### Gráfico del valor de la esperanza
•graf.esp=function(x,probs){
• esp=esperanza(x,probs)
• plot(x,probs,type="h",lwd=2,col=terrain.colors(8),
• ylim=c(-0.15,0.9),xlab="Recorrido",ylab="Probabilidad") # grafica la función de probabilidad
• points(esp,-0.07,pch=24,col="red")
• abline(0,0)# ubica el valor esperado
• title("Probabilidad puntual y valor esperado")}
•graf.esp(rec.x,prob.x) # aplica la función a la tirada de un dado
•graf.esp(c(1,2,8),c(0.2,0.2,0.6))

33. Muchas Gracias debiechan@gmail.com