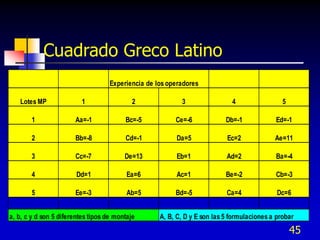
Este documento describe el análisis de varianza (ANOVA) para un factor principal y uno o más factores de bloqueo. Explica cómo realizar el ANOVA para un factor, un factor principal y un factor de bloqueo, y para diseños con cuadrados latinos y grecolatinos que incluyen dos o tres factores de bloqueo. También incluye ejemplos y cómo calcular las sumas de cuadrados, grados de libertad, cuadrados medios, estadísticos F y tomar decisiones sobre la igualdad de medias.

1. 1
ANOVA PARA UN FACTOR
PRINCIPAL Y UNO O MAS
FACTORES DE BLOQUEO
P. Reyes / Marzo 2003

2. 2
ANOVA - CONTENIDO
 ANOVA DE UN FACTOR O DIRECCIÓN
 ANOVA DE UN FACTOR Y UN FACTOR DE BLOQUEO
 ANOVA DE UN FACTOR Y DOS FACTORES DE
BLOQUEO – CUADRADO LATINO
 ANOVA DE UN FACTOR Y TRES FACTORES DE
BLOQUEO – CUADRADO GRECOLATINO

3. 3
ANOVA PARA UN FACTOR
O DIRECCIÓN

4. 4
ANOVA – Prueba de hipótesis para
probar la igualdad de medias de
varias poblaciones para un factor
diferentes
son
s
unas
A
Ha
Ho a
.
.
'
.
lg
:
.........
: 3
2
1




 



Se trata de probar si el efecto de un factor o
Tratamiento en la respuesta de un proceso o sistema es
Significativo, al realizar experimentos variando
Los niveles de ese factor (Temp. 1, Temp. 2, Temp.3, etc.)

5. 5
ANOVA - Condiciones
 Todas las poblaciones son normales
 Todas las poblaciones tiene la misma varianza
 Los errores son independientes con distribución
normal de media cero
 La varianza se mantiene constante para todos los
niveles del factor

6. 6
ANOVA – Ejemplo de datos
Niveles del Factor Peso % de algodón y Resistencia de tela
Peso porc. Respuesta
de algodón Resistencia de la tela
15 7 7 15 11 9
20 12 17 12 18 18
25 14 18 18 19 19
30 19 25 22 19 23
35 7 10 11 15 11

7. 7
ANOVA – Suma de
cuadrados total
Xij
Xij
Gran media
2
1
1
)
(

 



b
j
a
i
X
Xij
SCT

8. 8
ANOVA – Suma de cuadrados de
renglones (a)-tratamientos
Gran media
Media Trat. 1 Media Trat. a
Media trat. 2
a renglones




a
i
i X
X
b
SCTr
1
2
)
(

9. 9
ANOVA – Suma de cuadrados
del error
Media X1.
X1j
X3j
X2j
Media X2.
Media X3.
Muestra 1 Muestra 2 Muestra 3
2
1
1
)
( i
b
j
ij
a
i
X
X
SCE 
 
 


10. 10
ANOVA – Suma de cuadrados
del error
Media X1.
X1j
X3j
X2j
Media X2.
Media X3.
Muestra 1 Muestra 2 Muestra 3
SCTr
SCT
SCE 


11. 11
ANOVA – Grados de libertad:
Totales, Tratamientos, Error
a
n
a
n
SCE
gl
a
SCTr
gl
n
SCT
gl










)
1
(
)
1
(
.
1
.
1
.

12. 12
ANOVA – Cuadrados medios:
Total, Tratamiento y Error
)
/(
)
1
/(
)
1
/(
a
n
SCE
MCE
a
SCTr
MCTr
n
SCT
MCT







13. 13
ANOVA – Cálculo del estadístico
Fc y Fexcel
SCE
gl
SCTr
gl
ALFA
FINV
Fexcel
MCE
MCTr
Fc
.
,
.
,



14. 14
Tabla final de ANOVA
TABLA DE ANOVA
FUENTE DE VARIACIÓN SUMA DE GRADOS DE CUADRADO VALOR F
CUADRADOS LIBERTAD MEDIO
Entre muestras (tratam.) SCTR a-1 CMTR CMTR/CME
Dentro de muestras (error) SCE n-a CME
Variación total SCT n-1 CMT
Regla: Rechazar Ho si la Fc de la muestra es mayor que la F de Excel para una cierta alfa
o si el valor p correspondiente a la Fc es menor al valor de alfa especificado

15. 15
ANOVA – Toma de decisión
Fexcel
Fc
Alfa
Zona de rechazo
De Ho o aceptar Ha
Zona de no rechazo de Ho
O de no aceptar Ha
Distribución F

16. 16
ANOVA – Toma de decisión
Si Fc es mayor que Fexcel se rechaza Ho
Aceptando Ha donde las medias son diferentes
O si el valor de p correspondiente a Fc es
menor de Alfa se rechaza Ho

17. 17
ANOVA – Identificar las medias
diferentes por Prueba de Tukey T
Para diseños balanceado
(mismo número de columnas
en los tratamientos) el valor
de q se determina por medio
de la tabla en el libro de texto
b
CME
q
T a
n
a 
 ,
,


18. 18
ANOVA – Identificar las medias
diferentes por Prueba de Tukey T
Se calcula la diferencia Di entre cada par de Medias Xi’s:
D1 = X1 – X2 D2 = X1 – X3 D3 = X2 – X3 etc.
Cada una de las diferencias Di se comparan con el
valor de T, si lo exceden entonces la diferencia es
Significativa de otra forma se considera que las medias
Son iguales

19. 19
ANOVA – Identificar las medias
diferentes por Prueba de Diferencia
Mínima Significativa DMS
Para diseños balanceados (los tratamientos
tienen igual no. De columnas), se calcula un
factor DMS contra el que se comparan las
diferencias Xi – Xi’. Significativas si lo exceden
b
F
CME
DMS a
n
 ,
1
,
)
(
2 

20. 20
Prueba DMS para Diseños no
balanceados
a
n
a
k
j
k
j F
CME
b
b
DMS 










 ,
1
,
, )
(
1
1

Para diseños no balanceados (los
tratamientos tienen diferente no. De
columnas), se calcula un factor DMS
Para cada una de las diferencias Xi – Xi’

21. 21
ANOVA PARA UN FACTOR
PRINCIPAL Y UN FACTOR DE
BLOQUEO

22. 22
ANOVA – Prueba de hipótesis para
probar la igualdad de medias de
varias poblaciones con dos factores
Se trata de probar si el efecto de un factor o
Tratamiento en la respuesta de un proceso o sistema es
Significativo, al realizar experimentos variando
Los niveles de ese factor (Temp.1, Temp.2, etc.)
POR RENGLON
Y
Considerando los niveles de otro factor que se piensa
Que tiene influencia en la prueba – FACTOR DE BLOQUEO
POR COLUMNA

23. 23
ANOVA – Prueba de hipótesis para
probar la igualdad de medias de
varias poblaciones con dos factores
diferentes
son
s
unas
A
Ha
Ho a
.
.
'
.
lg
:
.........
: 3
2
1




 



diferentes
son
s
unas
A
Ha
Ho a
.
.
'
.
lg
:
'
.........
'
'
'
: 3
2
1




 



Para el tratamiento – en renglones
Para el factor de bloqueo – en columnas

24. 24
ANOVA 2 Factores - Ejemplo
Experienciaenaños delos operadores
Maquinas 1 2 3 4 5
Maq1 27 31 42 38 45
Maq2 21 33 39 41 46
Maq3 25 35 39 37 45

25. 25
ANOVA – Dos factores o
direcciones
 La SCT y SCTr (renlgones) se determina de la
misma forma que para la ANOVA de una
dirección o factor
 En forma adicional se determina la suma de
cuadrados del factor de bloqueo (columnas) de
forma similar a la de los renglones
 La SCE = SCT – SCTr - SCBl

26. 26
ANOVA de 2 factores – Suma de
cuadrados, gl. y Cuadrado medio
para el factor de bloqueo (en cols)
)
1
/(
1
.
)
( 2
1





 

b
SCBl
CMBl
b
SCBl
gl
X
X
a
SCBl j
b
j

27. 27
ANOVA de 2 factores – Suma de
cuadrados, gl. y Cuadrado medio
para el error
)
)(
/(
)
)(
(
.
b
n
a
n
SCBl
CME
b
n
a
n
SCE
gl
SCBl
SCTr
SCT
SCE










28. 28
ANOVA – Cálculo del estadístico
Fc y Fexcel
SCE
gl
SCTr
gl
ALFA
FINV
Fexcel
MCE
MCTr
Fc
.
,
.
,



29. 29
ANOVA de 2 factores – Cálculo del
estadístico Fcbl y Fexcel bloques
(columnas)
SCE
gl
SCBl
gl
ALFA
FINV
Fexcel
MCE
MCBl
Fc
.
,
.
,



30. 30
Tabla final ANOVA 2 Factores
FUENTE DE VARIACIÓN SUMA DE GRADOS DE CUADRADO VALOR F
CUADRADOS LIBERTAD MEDIO
Entre muestras (tratam.) SCTR a-1 CMTR CMTR/CME
Entre Bloques (Factor Bl) SCBl b-1 CMBL CMBL/CME
Dentro de muestras (error) SCE (a-1)(b-1) CME
Variación total SCT n-1 CMT
Regla: No rechazar si la F de la muestra es menor que la F de Excel para una cierta alfa

31. 31
ANOVA – 2 F. Toma de decisión
Fexcel
Fc
Tr o Bl
Alfa
Zona de rechazo
De Ho o aceptar Ha
Zona de no rechazo de Ho
O de no aceptar Ha
Distribución F

32. 32
ANOVA – 2 F. Toma de decisión
Si Fc (Tr o Bl) es mayor que Fexcel se rechaza
Ho Aceptando Ha donde las medias son
diferentes
O si el valor de p correspondiente a Fc (Tr o Bl)
es menor de Alfa se rechaza Ho

33. 33
Cálculo de los residuales
.
.
*
ˆ
ˆ
.
,
,
05
.
0
..
.
.
i
i
y
MSE
gl
k
k
y
ij
ij
ij
j
i
ij
s
r
R
b
MSE
s
y
y
e
y
y
y
y






 Y estimada
Error o residuo
Error estándar
Factor de comparación
Si la diferencia de medias excede a Rk es significativa

34. 34
Adecuación del modelo
 Los residuales deben seguir una recta en la gráfica
normal
 Deben mostrar patrones aleatorios en las gráficas de
los residuos contra el orden de las Yij, contra los
valores estimados y contra los valores reales Yij

35. 35
ANOVA PARA UN FACTOR
PRINCIPAL Y DOS O TRES
FACTORES DE BLOQUEO
CUADRADO LATINO Y
GRECOLATINO

36. 36
ANOVA – 3 y 4 factores
 El diseño de Cuadrado latino utiliza dos
factores de bloqueo adicionales al de
Tratamiento
 EL diseño de Cuadrado Grecolatino utiliza tres
factores adicionales al del Tratamiento
 El cálculo de suma de cuadrados para
renglones y para columnas es similar al de
ANOVA de un factor principal y otro de
bloqueo

37. 37
Cuadrado Latino
Añosexp. Turno
Empleado Mañana Tarde Noche
1 B=15 A=18 C=11
2 C=12 B=20 A=9
3 A=17 C=19 B=10
A,B,C =Máquinas1,2y3

38. 38
ANOVA – Cuadrado Latino:
Factor principal (A,B,C,D)
)
1
/(
1
1
.
)
( 2
1







 

b
SCTr
CMTr
b
a
SCTr
gl
X
X
a
SCTr Tr
b
j

39. 39
ANOVA – Cuadrado Latino: Cálculo
del error
)
1
)(
2
/(
)
1
)(
2
(
.
Re










a
a
SCE
CME
a
a
SCE
gl
SCTr
ng
SC
SCTcol
SCT
SCE

40. 40
ANOVA – Cálculo del estadístico
Fc y Fexcel
SCE
gl
SCTr
gl
ALFA
FINV
Fexcel
MCE
MCTr
Fc
.
,
.
,



41. 41
ANOVA – Cuadrado Latino Reng / Col
SCE
gl
SCBl
gl
ALFA
FINV
Fexcel
MCE
MCCols
Fcols
MCE
ng
MC
Fcreng
.
,
.
,
Re




42. 42
Tabla final ANOVA 2 Factores
FUENTE DE VARIACIÓN SUMA DE GRADOS DE CUADRADO VALOR F
CUADRADOS LIBERTAD MEDIO
Renglores SCRen a-1 CMRen CMRen/CME
Columnas SCCol b-1 CMCol CMCol/CME
Tratamiento SCTr a-1 CMTr CMTr/CME
Dentro de muestras (error) SCE (a-2)(a-1) CME
Variación total SCT n-1 CMT

43. 43
Cuadrado latino en Minitab
 Se introducen las respuestas en una columna C1
 Se introducen los subíndices de los renglones en una
columna C2
 Se introducen los subíndices de las columnas en una
columna C3
 Se introducen las letras mayúsculas que indican el
nivel del factor (A, B, C, D, etc.) correspondientes a
cada respuesta en la columna C4

44. 44
Cuadrado latino en Minitab
 Opción: ANOVA – General linear model
 En Response indicar la col. De Respuesta,
 En Model indicar las columnas de los factores y
 En Random factors indicar los factores adicionales al
del efecto principal a probar (A, B, C, D). Se pueden
pedir interacciones entre factores x – y con Cx*Cy
 Pedir gráfica de residuales Normal y vs fits y orden

45. 45
Cuadrado Greco Latino
Experiencia de los operadores
Lotes MP 1 2 3 4 5
1 Aa=-1 Bc=-5 Ce=-6 Db=-1 Ed=-1
2 Bb=-8 Cd=-1 Da=5 Ec=2 Ae=11
3 Cc=-7 De=13 Eb=1 Ad=2 Ba=-4
4 Dd=1 Ea=6 Ac=1 Be=-2 Cb=-3
5 Ee=-3 Ab=5 Bd=-5 Ca=4 Dc=6
a, b, c y d son 5 diferentes tipos de montaje A, B, C, D y E son las 5 formulaciones a probar

46. 46
Cuadrado Greco latino en Minitab
 Se introducen las respuestas en una columna C1
 Se introducen los subíndices de los renglones en una
columna C2
 Se introducen los subíndices de las columnas en una
columna C3
 Introducir los subíndices del factor adicional de letras
griegas con letras latinas minúsculas (a,b,c,d,e) en C4
 Se introducen las letras mayúsculas que indican el nivel
del factor (A, B, C, D, etc.) correspondientes a cada
respuesta en la columna C5

47. 47
Cuadrado Greco latino en Minitab
 Opción: ANOVA – General linear model
 En Response indicar la col. De Respuesta,
 En Model indicar las columnas de los factores y
 En Random factors indicar los factores adicionales al del
efecto principal a probar (A, B, C, D). También se
pueden indicar interacciones entre factores x-y con Cx *
Cy
 Pedir gráfica de residuales Normal y vs fits y orden

48. 48
ANOVA – Cuadrado Grecolatino
)
1
/(
1
.
)
( 2
1





 

b
SCG
CMG
b
SCG
gl
X
X
a
SCG m
b
m

49. 49
ANOVA de 2 factores – Suma de
cuadrados, gl. y Cuadrado medio
para el error
)
1
)(
3
/(
)
1
)(
3
(
.
Re











a
a
SCE
CME
a
a
SCE
gl
SCCol
n
SC
SCG
SCTr
SCT
SCE

50. 50
ANOVA – Cálculo del estadístico
Fc y Fexcel
SCE
gl
SCTr
gl
ALFA
FINV
Fexcel
MCE
MCG
Fc
.
,
.
,



51. 51
ANOVA – Cuadrado Grecolatino
SCE
gl
SCBl
gl
ALFA
FINV
Fexcel
MCE
MCTr
Fc
.
,
.
,



52. 52
Tabla final ANOVA 2 Factores
FUENTE DE VARIACIÓN SUMA DE GRADOS DE CUADRADO VALOR F
CUADRADOS LIBERTAD MEDIO
Renglores SCRen a-1 CMRen CMRen/CME
Columnas SCCol b-1 CMCol CMCol/CME
Letras griegas SCG a-1 CMG CMG/CME
Tratamiento SCTr a-1 CMTr CMTr/CME
Dentro de muestras (error) SCE (a-3)(a-1) CME
Variación total SCT n-1 CMT