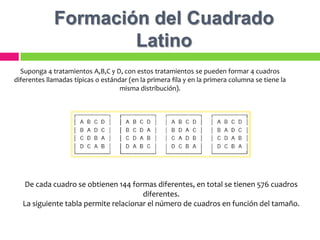
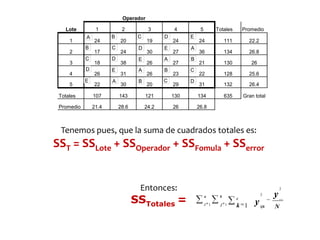
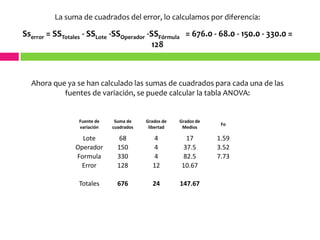
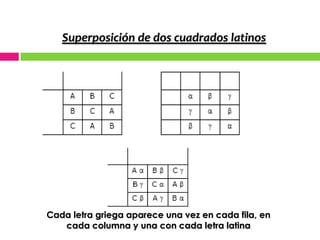
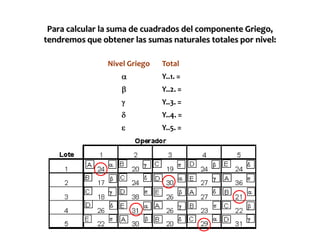
El documento describe dos diseños estadísticos: el diseño cuadrado latino y el diseño cuadrado grecolatino. El diseño cuadrado latino asigna tratamientos al azar en filas y columnas de manera que cada tratamiento aparece una vez en cada fila y columna. El diseño cuadrado grecolatino es similar pero incluye un cuarto factor llamado componente griego. El documento también presenta un ejemplo para ilustrar cómo se aplican estos diseños en un experimento sobre la explosividad de la dinamita.

1. ESTADÍSTICA IIDISEÑO CUADRADO LATINO Y GRECOLATINO

2. Diseño Cuadrado LatinoEl agrupamiento de las unidades experimentales en dos direcciones (filas y columnas) y la asignación de los tratamientos al azar en las unidades, de tal forma que en cada fila y en cada columna se encuentren todos los tratamientos constituye un diseño cuadrado latino.CARACTERÍSTICASLas unidades experimentales se distribuyen en grupos, bajo dos criterios de homogeneidad dentro de la fila y dentro de la columna y heterogeneidad en otra forma.

3. En cada fila y en cada columna, el número de unidades es igual al número de tratamientos.

4. Los tratamientos son asignados al azar en las unidades experimentales dentro de cada fila y dentro de cada columna.El numero de filas= al número de columnas= al número de tratamientos.

5. Los análisis estadísticos T-student, Duncan, Tuckey y en pruebas de contraste se procede como el diseño completo al azar y el diseño de bloques.

6. La desviación estándar de la diferencia de promedios y la desviación estándar del promedio, están en función del cuadrado medio del error experimental.Formación del Cuadrado LatinoSuponga 4 tratamientos A,B,C y D, con estos tratamientos se pueden formar 4 cuadros diferentes llamadas típicas o estándar (en la primera fila y en la primera columna se tiene la misma distribución).De cada cuadro se obtienen 144 formas diferentes, en total se tienen 576 cuadros diferentes.La siguiente tabla permite relacionar el número de cuadros en función del tamaño.

7. n = tamaño del cuadro.ASIGNACIÓN DE TRATAMIENTOSos tratamientos deben asignarse empleando uno de los cuadros de los posibles, es decir si son cuatro tratamientos, escoger entre los 576 posibles.MODELO ESTADÍSTICO

8. Tanto la hipótesis nula como la alternativa, siguen siendo las mismas, a saber:H0 : m1 = m2 =..........= maH1 : mi = mj para al menos un par ijEn este diseño, tenemos ahora, o queremos estudiar, cuatro fuentes de variación, la debida al Factor X, la debida al Factor Y, la causada por el Bloque(o Factor) Latino y la del error, por lo que nuestro modelo se puede expresar como:Yij= La i-esima observaciónm = Un parámetro General para todas las observaciones, llamado Media Globalti = El efecto del factor Xbj = El efecto del BloqueYlk = El efecto del bloque Latino

9. eij = El error experimentalContinuando con la metodología utilizada hasta aquí, reescribamos estas fuentes de variación, en términos de sumas de cuadrados:Sstotales = SSX + SSY + SSLatino + SSerrorEJEMPLOUn experimentador, desea probar en un arreglo cuadrado por bloques, que efecto tienen el factor lote de materia prima y el operador que prepara Dinamita, en la respuesta Explosividad de la misma. También desea bloquear el arreglo con la Formula que se utiliza para preparar la dinamita, para esto considera a el bloque Formula como su Factor o Bloque Latino. El arreglo queda como sigue (desea también probar 5 niveles):Un experimentador, desea probar en un arreglo cuadrado por bloques, que efecto tienen el factor lote de materia prima y el operador que prepara Dinamita, en la respuesta Explosividad de la misma. También desea bloquear el arreglo con la Formula que se utiliza para preparar la dinamita, para esto considera a el bloque Formula como su Factor o Bloque Latino. El arreglo queda como sigue (desea también probar 5 niveles):

10. Tenemos pues, que la suma de cuadrados totales es:SST = SSLote + SSOperador + SSFomula + SSerrorEntonces:SSTotales =

12. Bien, para calcular la suma de cuadrados del factor latino, utilizaremos el mismo mecanismo, solo que, como este factor latino se mueve de una manera diferente, necesitamos primero calcular los totales por nivel.

13. La suma de cuadrados del error, lo calculamos por diferencia:Sserror = SSTotales - SSLote -SSOperador -SSFórmula = 676.0 - 68.0 - 150.0 - 330.0 = 128Ahora que ya se han calculado las sumas de cuadrados para cada una de las fuentes de variación, se puede calcular la tabla ANOVA:

14. Utilizando un nivel de confianza del 95%, consultemos la F de las tablas de la distribución Fisher:Fa,g1,g2 -= F0.05, 4, 12 = 3.26,y esta es la misma para comparar contra la F calculada de las tres fuentes de variación, ya que estas tienen los mismos grados de libertad.Para el lote: Como la Fo (1.59) < F0.05, 4, 12 = 3.26, entonces se Acepta Ho, el lote de material no es fuente de variación para la respuesta.Para el Operador: Como la Fo (3.52) > F0.05, 4, 12 = 3.26, entonces se Rechaza Ho, el operador que prepara la dinamita, si influye en la explosividad de la misma.Para la Formula: Como la Fo (7.73) > F0.05, 4, 12 = 3.26, entonces se Rechaza Ho, la formula que se utiliza para preparar la dinamita, contribuye a la explosividad de la misma.

15. Diseño Cuadrado GrecolatinoEn los arreglos por bloques, se pueden analizar 4 factores, introduciendo un cuarto factor o bloque en un diseño cuadrado latino, siguiendo las mismas reglas utilizadas para introducir un tercer factor en un diseño cuadrado de dos factores. A este cuarto factor o bloque se le denomina componente griego, ya que se utilizan letras griegas para identificar sus niveles, a la adición de un diseño cuadrado latino y un cuarto factor, se le llama Diseño Cuadrado Greco-Latino.

16. Es un diseño con cuatro factores a k niveles

17. Se asume que no hay interacciones

18. Requiere k2 observaciones

19. El diseño factorial completo requiere k4

20. Cada nivel de un factor aparece una vez con cada nivel de los otros factores

21. Superposición de dos cuadrados latinosSuperposición de dos cuadrados latinosCada letra griega aparece una vez en cada fila, en cada columna y una con cada letra latina

22. El modelo es donde αi es el efecto fila, βj efecto columna, γk efecto De la letra latina y δl efecto de letra griega La notación yij (kl) indica que k y l dependen de ij.Tabla ANOVA

23. EjemploContinuemos con el ejemplo de la formulación de dinamita. El experimentador desea considerar La línea de ensamble en su diseño, ya que sospecha que estas son fuente de variación. Para hacer esto, decide utilizar un arreglo Cuadrado Greco-Latino, el cual se muestra a continuación (Por razones prácticas, se utilizaran los mismos datos que en el ejemplo anterior)

24. Ya que son los mismos datos del ejemplo anterior, los cálculos y resultados para las sumas de cuadrados para los componentes Lote, Operador, Fórmula y Suma Total son los mismos también: