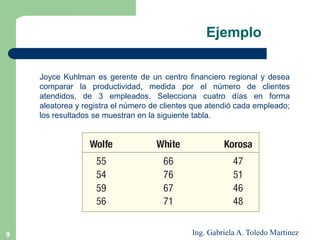
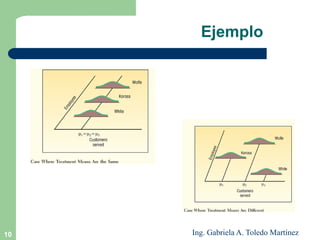
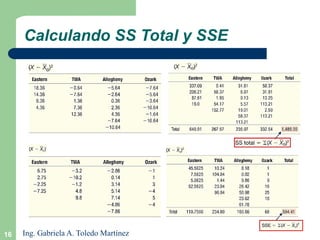
El documento describe el análisis de varianza (ANOVA), un método estadístico para comparar las medias de tres o más poblaciones. El ANOVA determina si las muestras podrían provenir de poblaciones con la misma media evaluando si la varianza entre las muestras es mayor que la varianza dentro de las muestras. El documento explica los supuestos del ANOVA, cómo calcular el estadístico F y tomar una decisión estadística, e incluye un ejemplo para ilustrar el proceso completo del ANOVA.















![19
Intervalo de confianza para la diferencia
entre dos medias
t es obtenido de la tabla t
con grados de libertad (n - k).
MSE = [SSE/(n - k)]
X X t MSE
n n
1 2
1 2
1 1
Ing. Gabriela A. Toledo Martínez](https://image.slidesharecdn.com/anovadeunfactor-230829043711-77e6d071/85/Anova-de-un-Factor-pdf-19-320.jpg)