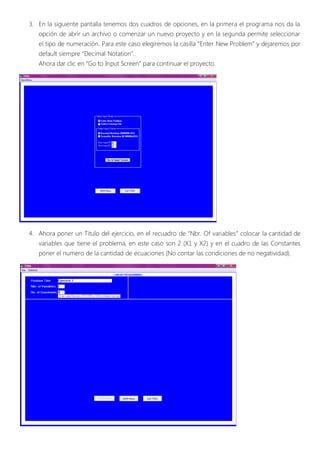
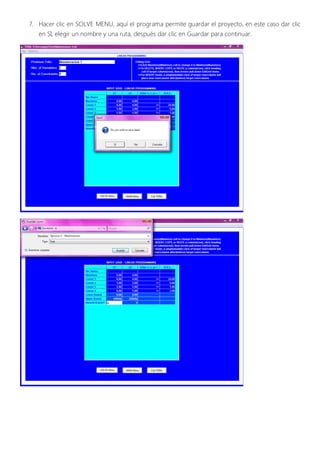
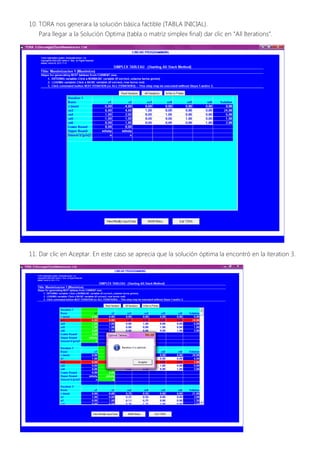
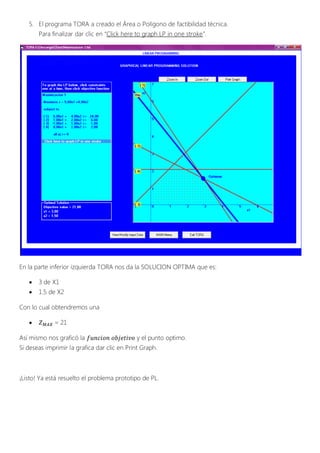
Este documento presenta un problema de programación lineal para maximizar la utilidad diaria de una empresa mediante la producción óptima de dos productos (X1 y X2) sujetos a restricciones en los insumos disponibles. Se formula el modelo matemático y se resuelve usando el software TORA, obteniendo como solución óptima 3 toneladas de X1 y 1.5 toneladas de X2 para una utilidad máxima de 21,000 USD. Adicionalmente, se verifica gráficamente la solución encontrada.

1. UNIVERSIDAD AUTÓNOMA DEL ESTADO DE MÉXICO
Aplicación de TORA
Aplicación de TORA para resolver problemas
de Programación Lineal
Autores:
Contreras Rodea Salvador
Gómez Simón Christian
Gallegos Hernández Alfredo
Meza Osnaya Adrián
2012
INVESTIGACIÓN DE OPERACIONES

2. Resolver problema prototipo de
Programación Lineal
Ejemplo 1 - Maximización
Planteamiento del Problema.
Toneladas de Materia Prima de
Concepto Producto X1 Producto X2 Disponibilidad
máxima diaria (TON)
Materia prima, M1 6 4 24
Materia prima, M2 1 2 6
Contribución o 5 4
Utilidad por Tonelada
(1,000 USD)
Condiciones o restricciones adicionales (Mercadotecnia)
1. Demanda máxima diaria para X2, 2 toneladas.
2. Demanda diaria de X2 no puede exceder a X1 por más de una tonelada.
La empresa solicita determinar la mezcla de producto óptima X1, X2, que maximice la utilidad total
diaria.

3. Pasos para resolver el problema de PL.
1. Leer y analizar el planteamiento del problema.
2. Formular el modelo matemático de PL.
2.1Función Objetivo.
2.2Restricciones o limitaciones.
2.3Condiciones de No negatividad.
3. Abrir TORA para resolver el problema.
Formulación del modelo matemático de PL.
1. Función objetivo.
=5 +4 ……………… (0)
2. Restricciones o limitaciones.
6 +4 ≤ 24 ……………… (1)
+ 2 ≤6 ……………… (2)
- + ≤1 ……………… (3)
≤2 ……………… (4)
3. Condiciones de No negatividad.
≥0
≥0

4. Obtener la solución del problema en TORA
Una vez teniendo los datos anteriores podemos resolver el problema con TORA, para ello seguir los
pasos explicados a continuación.
1. Abrir el programa TORA y dar clic en la opción CLIC HERE.
2. Hacerr clic en la opción “Linear Programming”.

5. 3. En la siguiente pantalla tenemos dos cuadros de opciones, en la primera el programa nos da la
opción de abrir un archivo o comenzar un nuevo proyecto y en la segunda permite seleccionar
el tipo de numeración. Para este caso elegiremos la casilla “Enter New Problem” y dejaremos por
default siempre “Decimal Notation”.
Ahora dar clic en “Go to Input Screen” para continuar el proyecto.
4. Ahora poner un Titulo del ejercicio, en el recuadro de “Nbr. Of variables” colocar la cantidad de
variables que tiene el problema, en este caso son 2 (X1 y X2) y en el cuadro de las Constantes
poner el numero de la cantidad de ecuaciones (No contar las condiciones de no negatividad).

6. 5. Presionar ENTER para que el programa cree la tabla inicial.
6. En la primera fila puedes ponerle nombre a las variables X1 y X2, para este caso lo dejarlo así, en
las filas y columnas de abajo copiar las ecuaciones 0, 1, 2, 3 y 4. Ahora las filas correspondientes
a “Lower, Upper Bound y Unrests’d” dejarlas como están.

7. 7. Hacer clic en SOLVE MENU, aquí el programa permite guardar el proyecto, en este caso dar clic
en SI, elegir un nombre y una ruta, después dar clic en Guardar para continuar.

8. 8. En la siguiente ventana se encuentran opciones para resolver el problema, primero
obtenendremos el resultado Algebraico y lo resolveremos por el método “All-slack starting
solution”.
9. En la siguiente ventana dar clic en “Go To Output Screen”.

9. 10. TORA nos generara la solución básica factible (TABLA INICIAL).
Para llegar a la Solución Optima (tabla o matriz simplex final) dar clic en “All Iterations”.
11. Dar clic en Aceptar. En este caso se aprecia que la solución óptima la encontró en la iteration 3.

10. 12. Interpretar resultados.
La solución básica factible es
 3 de X1
 1.5 de X2
Con lo cual obtendremos una
 = 21
TORA obtuvo dos variables de holgura con
 = 2.50
 = .50

11. Verificar el resultado mediante el método GRAFICO.
1. Hacer clic en VIEW/MODIFY Input Data. A continuación se abrirá la ventana de abajo, entonces
dar clic en:
Solve Problem / Graphical.
2. Dar clic en Go To Output Screen para generar la grafica.

12. 3. A continuación se puede observar en la parte izquierda tenemos las ecuaciones que ya
habíamos creado.
4. Para ver cada línea correspondiente a las ecuaciones dar clic sobre cada ecuación para que
aparezca en la grafica, hacer clic de la ecuación 1 a la 4.

13. 5. El programa TORA a creado el Área o Polígono de factibilidad técnica.
Para finalizar dar clic en “Click here to graph LP in one stroke”.
En la parte inferior izquierda TORA nos da la SOLUCION OPTIMA que es:
 3 de X1
 1.5 de X2
Con lo cual obtendremos una
 = 21
Así mismo nos graficó la y el punto optimo.
Si deseas imprimir la grafica dar clic en Print Graph.
¡Listo! Ya está resuelto el problema prototipo de PL.