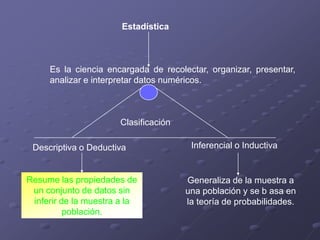
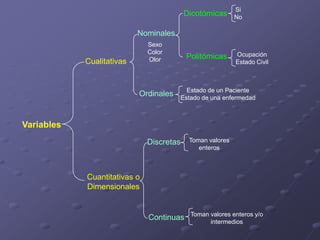
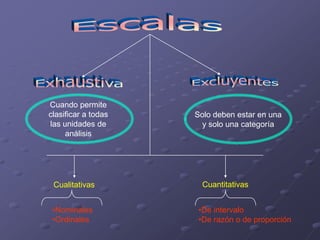
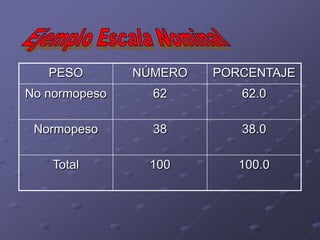
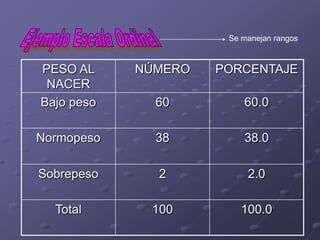
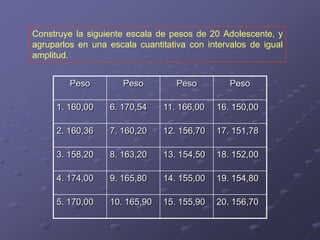
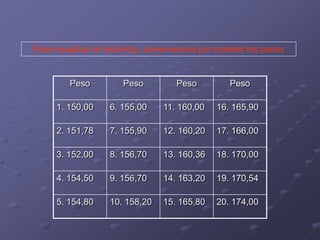
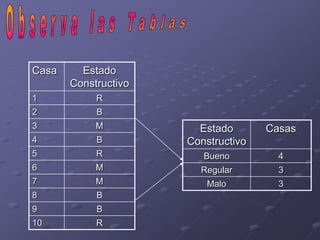
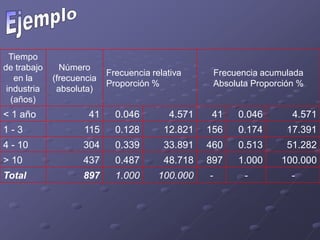
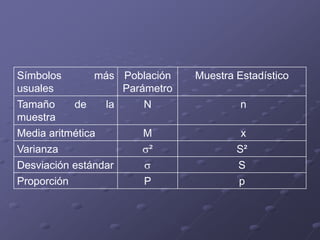
Este documento presenta los objetivos y contenidos de un tema sobre estadística. Los objetivos incluyen clasificar variables, identificar universos y muestras, y construir escalas y distribuciones de frecuencia. Explica conceptos como variables cualitativas y cuantitativas, universos y muestras, y cómo construir escalas cuantitativas con intervalos de igual amplitud.

2. Tema I.- Generalidades
Objetivos:
Clasificar distintos tipos de variables según su naturaleza,
mediante su reconocimiento, para facilitar su manejo en la
investigación empírica en la atención primaria de salud.
Identificar el universo y la muestra en diversas situaciones,
mediante la presentación de ejemplos, para su utilización en
la investigación empírica en la atención de salud.
Construir escalas de intervalos de igual amplitud, mediante
procedimientos estadísticos establecidos, para su utilización
en la construcción de cuadros y gráficos estadísticos útiles en
el trabajo de la atención primaria de salud.

3. Objetivos:
Construir escalas de intervalos de igual amplitud, mediante
procedimientos estadísticos establecidos, para su utilización
en la construcción de cuadros y gráficos estadísticos útiles en
el trabajo de la atención primaria de salud.
Construir distribuciones de frecuencia, mediante
procedimientos estadísticos establecidos, para su utilización
en la construcción de cuadros y gráficos estadísticos útiles
en el trabajo de atención primaria de salud.

4. Estadística
Es la ciencia encargada de recolectar, organizar, presentar,
analizar e interpretar datos numéricos.
Clasificación
Descriptiva o Deductiva Inferencial o Inductiva
Resume las propiedades de Generaliza de la muestra a
un conjunto de datos sin una población y se b asa en
inferir de la muestra a la la teoría de probabilidades.
población.

5. Variable
Es una característica susceptible de ser medida en las unidades
de análisis que se estudian, que toma diferentes valores o grados
de intensidad, en dependencia de cuál sea la unidad de medida
Colores de las Sexo.
cosas. Total de autos
Estatura. Volumen de los
Altura de recipientes.
edificios. Etc.

6. Ejemplo:
Supongamos que unos investigadores de cierta área de salud
investigan la presencia de discapacidad física en ancianos de una
comunidad. Para ello, miden en cada anciano escogido las variables:
•Sexo
•Raza
•Sensación de inactividad
•Número de consultas médicas recibidas
•Edad.
Variables Cualitativas Variables Cuantitativas
(no pueden medirse numéricamente) (si pueden medirse numéricamente)
•Color •Peso
•Olor •Edad
•Sexo •Talla
•Si Juan es o no es •Número de hijos
alcohólico •Etc.

7. Si
Dicotómicas No
Nominales
Sexo
Color Ocupación
Olor Politómicas
Cualitativas Estado Civil
Estado de un Paciente
Ordinales Estado de una enfermedad
Variables
Discretas Toman valores
enteros
Cuantitativas o
Dimensionales
Toman valores enteros y/o
Continuas intermedios

8. Universo o Población
Entendemos un grupo, casi siempre numeroso, compuesto frecuentemente
pero no necesariamente por personas, que tienen en común al menos una
característica susceptible de ser investigada. De ella se extraen las muestras
necesarias para su estudio.
Muestra
Es el subgrupo de una población extraído por un investigador para extraer
conclusiones de la misma, o para realizar estimaciones sobre ella. La muestra
se obtiene mediante el muestreo.

9. Para determinar si el medicamento X producido en la fábrica
de medicamento Y tiene la calidad adecuada, se toman 100
tabletas al azar de la producción de una semana. Aquí la
población es el total de tabletas del medicamento X producidas
por la fábrica, y la muestra está formada por las 100 tabletas
que se estudiaron.
Un grupo de investigadores desea estudiar el comportamiento
del síndrome anémico en el área que atiende el policlínico Sur
de la provincia Guantánamo, para ello decide tomar a los
habitantes de los consultorios 66, 50, 15 y 5 a fin de realizares
los exámenes pertinentes. En este caso, la población está
formada por el total de personas que atiende el policlínico, y la
muestra por las personas que atienden los cuatro consultorios
escogidos.

10. Unos investigadores se proponen estudiar la actitud de los
jubiladas de cierto consultorio ante el estrés generado por las
tareas del hogar, por lo que estudiaron a 10 de las 37 jubiladas
existentes. Obviamente, la población está constituida por las
37 jubiladas, y la muestra por las 10 señoras estudiadas.
Los mismos investigadores desean estudiar el fenómeno en el
área atendida por el policlínico, de ahí estudiaran a las
jubiladas de cinco consultorios. Ahora, la población es el total
de jubiladas que atiende el policlínico, y la muestra las
jubiladas de aquellos consultorios escogidos.

11. Cuando permite
clasificar a todas Solo deben estar en una
las unidades de y solo una categoría
análisis
Cualitativas Cuantitativas
•Nominales •De intervalo
•Ordinales •De razón o de proporción

12. PESO NÚMERO PORCENTAJE
No normopeso 62 62.0
Normopeso 38 38.0
Total 100 100.0

13. Se manejan rangos
PESO AL NÚMERO PORCENTAJE
NACER
Bajo peso 60 60.0
Normopeso 38 38.0
Sobrepeso 2 2.0
Total 100 100.0

14. Se debe mantener las características de una escala ordinal, en
está conoces las distancias entre dos números de la escala.
Ejemplo, Temperatura (Celsius y Fahrenheit).
Si una escala posee las características antedichas, pero con la
diferencia de que se origine en un cero real, entonces la misma
es una

15. Compuesta por varias divisiones ordenadas llamadas intervalo
de clase (IC), los cuales están delimitados por límites de clase,
que son los valores mayor y menor que los enmarcan.
Escala cuantitativa abierta
Edad Intervalo de clase abierto
< 15 años
15 – 19 años
20 – 24 años
25 y más años Intervalo de clase abierto

16. Límite Real (LR)
(LRS) (LRI)
La amplitud o recorrido (A) de un intervalo de clase es la
longitud de éste. Su cálculo puede hacerse de distintas
maneras:
1. Diferencia entre los LR del intervalo en cuestión. En el
ejemplo anterior, los LR del segundo IC son 14.5 y 19.5 por
lo que la amplitud es 5.
2. Encontrar la diferencia de los limites de clase del intervalo
de referencia y, luego, adicionarle una unidad al resultado
obtenido. A=(19-15)+1=5.
3. Calcular A contando los números enteros que se encuentran
entre los valores límites. “conteo de “ 15,16,17,18,19, es
decir A=5.

17. La marca de clase de un IC es el punto medio de dicho
intervalo, que se calcula mediante la semisuma de los límites
de clase del intervalo referido. Ejemplo, la marca de clase del
tercer intervalo es MC = ( 20 + 24 ) / 2 = 22.

18. 1. Determinar el recorrido de la serie (R). Esto lo logras restando el valor
mínimo al máximo.
2. Fija el número mínimo de intervalos de clase deseado. Esta decisión va por
ti, lo determinarás en dependencia a tus necesidades.
3. Calcula la amplitud (A) de los intervalos. Para ello, divide el recorrido
que obtuviste en el paso 1 por el número que fijaste en el paso anterior.
4. Delimita los límites inferiores (LI) de los intervalos. Partiendo del valor mínimo
de la serie, añádele la amplitud y tendrás el LI del intervalo siguiente, a este
le sumas la amplitud y tendrás el subsiguiente, y así hasta llegar al último LI
de la lista.
5. Delimita los límites superiores (LS). Lo harás sustrayendo una unidad al LI
siguiente. En el caso del LS del último intervalo, lo obtendrás sumándole la
amplitud al último LI, luego restando al resultado una unidad.

19. Construye la siguiente escala de pesos de 20 Adolescente, y
agruparlos en una escala cuantitativa con intervalos de igual
amplitud.
Peso Peso Peso Peso
1. 160,00 6. 170,54 11. 166,00 16. 150,00
2. 160,36 7. 160,20 12. 156,70 17. 151,78
3. 158,20 8. 163,20 13. 154,50 18. 152,00
4. 174,00 9. 165,80 14. 155,00 19. 154,80
5. 170,00 10. 165,90 15. 155,90 20. 156,70

20. Para visualizar el recorrido, comencemos por ordenar los pesos
Peso Peso Peso Peso
1. 150,00 6. 155,00 11. 160,00 16. 165,90
2. 151,78 7. 155,90 12. 160,20 17. 166,00
3. 152,00 8. 156,70 13. 160,36 18. 170,00
4. 154,50 9. 156,70 14. 163,20 19. 170,54
5. 154,80 10. 158,20 15. 165,80 20. 174,00

21. Observe el valor mínimo es 150,00 y el máximo 174,00 , la escala
se construiría de la siguiente manera.
1. El recorrido de la serie es R = 174,00 – 150,00 = 24
2. Supongamos que deseas como mínimo 4 IC
3. La amplitud que tendrán los intervalos es A = 24 / 4 = 6
4. Límites inferiores:
IC LI
1. 150
2. 150 + 6 = 156
3. 156 + 6 = 162
4. 162 + 6 = 168
5. Límites superiores:
IC Ls
1. 156 - 1 = 155
2. 162 - 1 = 161
3. 168 - 1 = 167
4. 174 - 1 = 173

22. Escalas obtenidas:
150 -155
156 -161
162 -167
168 -173
Límite inferior del quinto IC: 168 + 6 = 174
Límite superior del último intervalo: 174 + 6 – 1 = 179
150 -155
156 -161
162 -167
168 -173
174 -179

25. Número de casos dentro de una clase o
intervalos, puede ser absoluta o relativa.

26. Es el modo en que se distribuyen las
unidades de análisis entre las clases o
categorías que conforman la escala de
clasificación de la variable en cuestión.

27. Casa Estado
Constructivo
1 R
2 B
3 M Estado Casas
4 B Constructivo
5 R Bueno 4
6 M Regular 3
7 M Malo 3
8 B
9 B
10 R

28. Absoluta
Relativa
Acumulada
Absoluta Relativa

29. Es el resultado de contar los
casos y/o observaciones, que
Frecuencia Absoluta corresponden a cada una de las
clases o categorías de la escala
de clasificación.
Es la importancia o peso relativos
Frecuencia relativa que tienen las unidades de
análisis de una categoría o clase
sobre el total de las unidades.
Son las frecuencias absolutas o
Frecuencia acumuladas relativas que se acumulan hasta
un intervalo de clase dado.

30. Absoluta
Se obtiene contando los casos u
observaciones.
Relativa
Se calcula dividiendo la frecuencia absoluta de la clase en cuestión por el
total de observaciones, en cuyo caso obtendrás una proporción. Si
multiplicaste este resultado por 100, obtendrás un porcentaje.
Acumuladas
Se calculan sumando las frecuencias A o R hasta la clase deseada. La FA para el
último IC será el total de observaciones, si se tratare de la FAA, y si fuera el caso de
la relativa, entonces será 1 o 100, en dependencia de si usaste proporción o
porcentaje.

31. Tiempo
de trabajo Número
Frecuencia relativa Frecuencia acumulada
en la (frecuencia
Proporción % Absoluta Proporción %
industria absoluta)
(años)
< 1 año 41 0.046 4.571 41 0.046 4.571
1-3 115 0.128 12.821 156 0.174 17.391
4 - 10 304 0.339 33.891 460 0.513 51.282
> 10 437 0.487 48.718 897 1.000 100.000
Total 897 1.000 100.000 - - -

32. Una de las características más sobresalientes de la distribución de datos es su
tendencia a acumularse hacia el centro de la misma. Esta característica se
denomina Tendencia central, entonces las MTC son las que representan a un
conjunto de datos.
Las medidas de tendencia central más usuales son
Media aritmética (x), el valor medio.
Mediana, el valor central.
Moda, el valor más frecuente.

33. Es aquella que se define como el promedio de un conjunto de datos.
La media Aritmética sumando todos los valores en una población o muestra
y se divide entre el número de valores sumados.
Para obtener la edad promedio de la población de 100 pacientes registrados
en la siguiente tabla se procede de la siguiente forma:
10, 22, 24, 42, 37, 77, 89, 85, 28, 63, 9, 10, 7, 51,2, 1, 52, 7, 48, 54, 32, 29, 2,
15, 46, 48, 39, 6, 72, 14, 36, 69, 40, 61, 12, 21, 54, 53, 58, 32, 27, 33, 1, 25,
22, 6, 81, 11, 56, 5, 63, 53, 88, 48, 52, 87, 71, 51, 52, 33, 46, 33, 85, 22, 5, 87,
28, 2, 85, 61, 16, 42, 69, 7, 10, 53, 33, 3, 85, 8, 51, 60, 58, 9, 14, 74, 24, 87, 7,
81, 30, 76, 7, 6, 27, 18, 17, 53, 70, 49.

34. Ejemplo
66, 100, 98, 96, 58, 94, 90
= 66, 100, 98, 96, 58, 94, 90 = 602 = 86
X 7 7
n
∑ xi
i=1
x= n

35. La mediana de un conjunto finito de valores es aquel valor que divide al
conjunto en dos partes iguales, de forma que el número de valores
mayor o igual a la mediana es igual al número de valores menores o
iguales a ésta.

36. 1. Sí el número de valores es impar, la mediana es el valor medio siempre
y cuando todas las variables sean arreglas en magnitudes de mayor a
menor.
2. Cuando el número de valores en el conjunto es par, no existe un solo
valor medio, sino que existen dos valores medios, en tal caso, la
mediana corresponde a la media de esas dos magnitudes.

37. Tomaremos como ejemplo los datos anteriores, en ella los valores deberán
estar ordenados, de modo que sólo se requiere encontrar los dos valores
medios. Éstos corresponden a los valores 36 y 37 , y la mediana, por lo
tanto, es ( 36 + 37 ) / 2 = 36.5.

38. OjO
Si el conjunto de datos tiene un número impar de observaciones, la posición de la
mediana es;
n+1
Posición de la mediana =
Ejemplo: 2
45, 52, 56, 67, 67 (Impar)
M=(5+1)/2=3
35, 45, 52, 56, 67, 67 (Par)
M = ( 6 + 1 ) / 2 = 3.5 Se promedian los valores 3 y 4

39. Obténgase ahora la mediana para la muestra que contiene los valores 10,
54, 21, 33, y 53.
Al ordenar estos datos de menor a mayor se obtendrá la secuencia 10, 21,
33, 53, y 54. puesto que se trata de un número impar de valores, la
mediana corresponda con el valor medio, es decir 33.

40. La moda de un conjunto de valores es aquel valor que ocurre con mayor
frecuencia. Si todos los valores son diferentes, no hay moda. Por otra
parte, un conjunto de valores puede tener más de una moda.
Nuevamente, al observar el ejemplo anterior, se encuentra que el 7
ocurre cinco veces, siendo el que ocurre con mayor frecuencia,
correspondiendo entonces a la moda.

41. Para ilustrar un conjunto de valores que tienen más de una moda,
considérese un laboratorio con diez empleados cuyas edades son 20, 21,
20, 20, 34, 22, 24, 27, 27 y 27. se puede decir que estos datos tienen dos
modas 20 y 27.
Una muestra que consista de los valores 10, 21, 33, 53 y 54. encontrar la
moda.
No tiene moda, puesto que todos los valores son diferentes.

42. Símbolos más Población Muestra Estadístico
usuales Parámetro
Tamaño de la N n
muestra
Media aritmética M x
Varianza ² S²
Desviación estándar S
Proporción P p