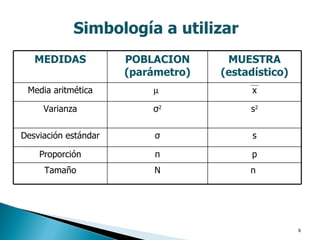
Este documento introduce conceptos básicos de estadística, incluyendo las diferencias entre estadística descriptiva e inferencial, y las definiciones de población, muestra, unidad de análisis, parámetro, estadístico, y escalas de medición como nominal, ordinal, de intervalo y de razón. También presenta ejemplos ilustrativos de variables cualitativas y cuantitativas, y las distintas escalas de medición.

1. INTRODUCCION. CONCEPTOS BASICOS Dra. Luz Carbajal A Setiembre, 2010 Departamento de Estadística, Demografía, Humanidades y Ciencias Sociales

2. La Estadística estudia los métodos científicos para recoger, organizar, resumir y analizar datos, así como para sacar conclusiones válidas y tomar decisiones razonables basadas con tal análisis.

3. Descriptiva Sistematizar, recolectar, ordenar y presentar los datos respecto a un fenómeno que presenta variabilidad o incertidumbre para su estudio y describirla. Inferencial Deducir las leyes que rigen esos fenómenos y poder realizar predicciones sobre los mismos, tomar decisiones u obtener conclusiones a partir de una muestra . n N Areas de la Estadística:

4. Población: Conjunto de todos los individuos que son susceptibles a ser estudiados. Muestra: Subconjunto de la población y que tenemos acceso para realizar el estudio. Debe tener ciertas características que la definen como representativa de la población a estudiar. Unidad de análisis: Individuo del cual se obtiene la información. Marco Muestral : Es el listado de todos los individuos susceptibles a ser estudiados (población de estudio)

5. Dato: valor aislado de una variable Parámetro: Es una medida estadística (un valor) que resume los datos de una población. Es un valor fijo para la población en estudio. Estadístico: es una medida estadística que resume los datos de una muestra. Es un valor variable.

6. Simbología a utilizar MEDIDAS POBLACION (parámetro) MUESTRA (estadístico) Media aritmética  x Varianza σ 2 s 2 Desviación estándar σ s Proporción π p Tamaño N n

7. Población: Pacientes del servicio de cardiología del Hospital María Auxiliadora del 2009. Se tiene interés en conocer en esta población: Frecuencia cardiaca promedio  (  ) Proporción de pacientes que consumía tabaco  (  ) En este caso  y  se consideran parámetros y para conocer sus valores debemos estudiar toda la población de pacientes del servicio del 2009. Si el estudio se realiza mediante una muestra, se calcula estadísticos como: media aritmética (  x ), desviación estándar (s) y proporción (p). Veamos algunos ejemplos de medidas estadísticas: Ejemplo:

8. Variables estadísticas : Variable : Cualquier característica de una persona, medio ambiente o situación experimental, que puede variar de persona a persona, de un medio ambiente a otro, o de una situación experimental a otra. Clasificación: Variable cualitativa (categórica) . Característica que se expresa cualitativamente. Ejm: Género, raza, estado nutricional, estado civil, etc. Puede ser dicotómica o politómica Variable cuantitativa (numérica) . Característica que se expresa cuantitativamente Ejm: edad, peso, número de atenciones, etc Puede ser discreta (enteros) o continua (decimales)

9. Población: Niños de 5 a 10 años de edad Variables: Peso - Frecuencia respiratoria Talla - Género Obesidad - Nº de hermanos Perímetro abdominal - Lugar de procedencia Variables cualitativas : Dicotómica : Género, obesidad; Politómica : Lugar de procedencia; Variables cuantitativas : Discretas : Nº de hermanos, frec. resp. Continuas : Peso, talla, perímetro abdominal

10. Escalas de medición: Nominal, ordinal, de intervalo y de razón Nominal .- Para cada unidad de análisis se determina la pertenencia a una entre dos o más categorías excluyentes. No es posible establecer relación de orden entre las categorías. Si se usan números estos cumplen la propiedad de = ó  . Ejm: Sexo, estado civil, procedencia, área de desempeño laboral, grupo sanguíneo, presencia o ausencia de un atributo, etc.

11. Ordinal .- Se determina la pertenencia de las unidades de análisis a categorías excluyentes, pero existe un grado de intensidad de la propiedad medida, por lo que las categorías guardan un orden. Los números cumplen con la propiedad de =,  , < y >. Ejm: Clase social (A, M, B), opinión sobre una propuesta política (TA, A, I, D, TD), nivel de dependencia (TD, MD, TI), Escalas médicas (apgar, EVA para medir dolor, etc)

12. Veamos los ejemplos: Escala nominal Sexo : Masculino (M) (1) (1)  (2), si Femenino (F) (2) Estado civil : Soltero (S) (1) (1)  (4), si; Casado (C) (2) pero (4) >(1), no. Viudo (V) (3) Divorciado (D) (4) Conviviente (Co) (5) Separado (Se) (6)

13. Escala ordinal Dolor : Leve (1) (1)  (2), si; (1) < (2),si Moderado (2) Intenso (3) Nivel de instrucción : Primaria (1) Secundaria (2) Superior (3)

14. De intervalo .- Se asignan números a cada elemento para indicar la intensidad de una característica, con unidad de medida y origen arbitrarios, que se elige en base a conveniencias prácticas. El cero es relativo. Entre dos números consecutivos se puede calcular una diferencia. Signos utilizables: =,  ,  ,  , +, y –

15. De razón .- Se asignan números a los elementos para indicar la intensidad de una característica con unidades de medida y de origen fijo, manteniendo la igualdad de las proporciones. El cero es absoluto. Signos útiles: además de los anteriores, el signo de la división ÷

16. Escala de intervalo (origen arbitrario) Temperatura en ºC Origen: 0 ºC (cero relativo) Puntajes de pruebas educativas y psicológicas (cero relativo). Años calendarios transcurridos (cero relativo). La diferencia entre 40º y 35ºC y entre 25º y 30º es igual tanto, numéricamente como respecto al atributo ( cantidad de calor)

17. Escala de razón (origen y cero absolutos) peso - plomo en sangre talla - presión arterial frecuencia cardiaca ingresos - gastos Si José gana 6 mil y César 3 mil, no sólo podemos afirmar que José gana 3 mil más que César, sino además que José gana el doble que César.