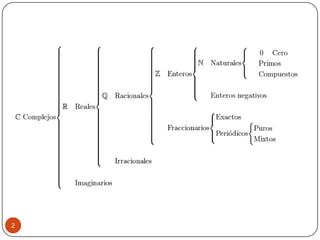
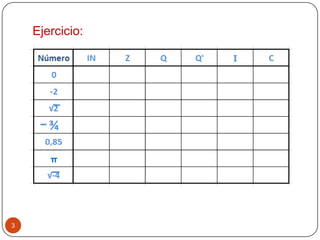
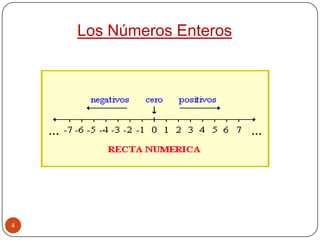
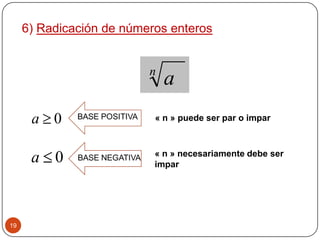
El documento proporciona información sobre los números enteros, incluidas sus propiedades y operaciones. Explica cómo sumar, restar, multiplicar, dividir y elevar números enteros a una potencia usando las reglas de los signos. También introduce los números irracionales y reales, y explica cómo representarlos y realizar operaciones básicas con ellos.