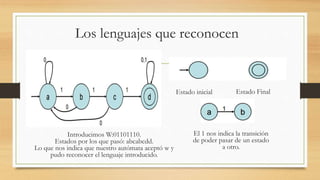
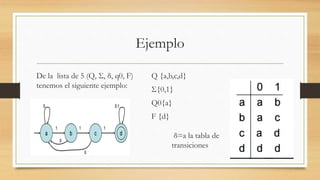
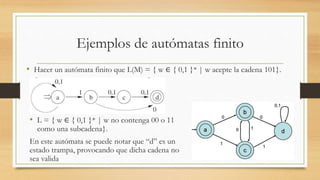
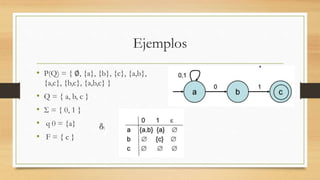
Este documento describe los autómatas finitos, incluyendo su estructura, operaciones y ejemplos. Un autómata finito es un modelo computacional que realiza cálculos automáticos sobre una entrada para producir una salida. Está compuesto por un alfabeto, un conjunto finito de estados, una función de transición, un estado inicial y un conjunto de estados finales. El documento también explica operaciones lingüísticas como la unión, intersección y concatenación en autómatas finitos.

1. Autómata finito
Pedro Jiménez 16-0588

2. Objetivos
• Poder dar a entender que son los autómatas finitos.
• Presentar ejemplos de ellos para su mejor entendimiento.
• Ver su uso.
• Ver sus operaciones y su utilización del lenguaje
• Etc.

3. Autómata finito
• Un autómata finito (AF) o máquina de estado finito es un modelo
computacional que realiza cómputos en forma automática sobre una entrada para
producir una salida.
• Este modelo está conformado por un alfabeto, un conjunto de estados finito, una
función de transición, un estado inicial y un conjunto de estados finales.

4. Los lenguajes que reconocen
Estado inicial Estado Final
Introducimos W:01101110.
Estados por los que pasó: abcabcdd.
Lo que nos indica que nuestro autómata aceptó w y
pudo reconocer el lenguaje introducido.
El 1 nos indica la transición
de poder pasar de un estado
a otro.

5. Puntos generales
• El autómata acepto “w” debido a que llego a su estado final y aun se mantiene allí.
• El conjunto de transiciones o alfabetos se representa por “Σ” que en este caso es: Σ
= { 0,1}, debido a que solo 0 y 1 son nuestras posibles transiciones.
• La longitud de w es | w |.
• “ε” representa una entrada vacía.
• L(M): Es el lenguaje aceptado por el autómata: { w | w es aceptado por M }.

6. Autómata finito
Está formato por una lista de 5 (Q, Σ, δ, q 0, F) donde:
• Q es la cantidad finita de estados.
• Σ es la cantidad finita de alfabeto.
• δ=Q ×Σ→ Q donde esta es la function de transición. Esta formada por el estado, la
transición y el estado que esta justo con esa transición. Esta puede ser representado
por tablas.
• q0 es el estado inicial.
• F es el estado final.

7. Ejemplo
De la lista de 5 (Q, Σ, δ, q0, F)
tenemos el siguiente ejemplo:
Q {a,b,c,d}
Σ{0,1}
Q0{a}
F {d}
δ=a la tabla de
transiciones

8. Ejemplos de autómatas finito
• Hacer un autómata finito que L(M) = { w ∈ { 0,1 }* | w acepte la cadena 101}.
• L = { w ∈ { 0,1 }* | w no contenga 00 o 11
como una subcadena}.
En este autómata se puede notar que “d” es un
estado trampa, provocando que dicha cadena no
sea valida

9. Operaciones del lingüísticas
Estas son operaciones que nos permiten construir lenguajes a partir de otros lenguajes.
Entre las operaciones tenemos:
• La union: L1 ∪ L 2.
• Intersección: L1 ∩ L 2 .
• Complemento: L c.
• Establecer diferencia: L1 - L 2
• También tenemos operaciones especialmente para los strings:
• Concatenation: L1 ◦ L2 o solo L1 L 2.
• Star: L*

10. Concatenación
• L 1 ◦ L2 = { XY | X ∈ L 1 y Y ∈ L2 }
• El objetivo es poner los strings (digito o cadena aceptada) de cada lenguaje y
concatenarlos.
Ejemplo:
• Σ = { 0, 1 }, L1 = { 0, 00 }, L2 = { 01, 001 }
• L1 ◦ L2 = { 001, 0001, 00001 }

11. Operación de estrella
• L* = { x | x = Y1 Y2 … Yk para algún k ≥ 0, donde cada Y esta en L }
• =L0 ∪ L1 ∪ L2 ∪ …está en L* por cada L, desde que esto es L0
• ε.
Ejemplos:
• ¿Que es ∅* ?
• Se aplica la definición:
∅* = ∅0 ∪ ∅1 ∪ ∅2 ∪ …
El resto de ∅1 ∪ ∅2 es ∅, por lo que el resultado es ε debido a que L 0 = { ε }.

12. Operación estrella
Ejemplos:
• ¿Que es { a }*?
• Se aplica la definición:
Abreviar todo esto solo para { a }*.
Ejemplos:
• ¿Que es Σ*?
• Se aplica la definición:

13. Autómata finito no determinístico
• Un autómata finito determinista (abreviado AFD) es un autómata
finito que además es un sistema determinista; es decir, para cada estado en
que se encuentre el autómata, y con cualquier símbolo del alfabeto leído,
existe siempre no más de una transición posible desde ese estado y con ese
símbolo.

14. Autómata finito determinista
Está formato por una lista de 5 (Q, Σ, δ, q 0, F) donde:
• Q es la cantidad finita de estados.
• Σ es la cantidad finita de alfabeto.
• Q × Σ ε → P(Q) donde esta es la function de transición. Esta formada por el
estado, la transición y el estado que esta justo con esa transición. Esta puede ser
representado por tablas.
• q0 ∈ Q= es el estado inicial.
• F ⊆ Q= es el estado final.

15. Ejemplos
• P(Q) = { ∅, {a}, {b}, {c}, {a,b},
{a,c}, {b,c}, {a,b,c} }
• Q = { a, b, c }
• Σ = { 0, 1 }
• q 0 = {a}
• F = { c }
δ: