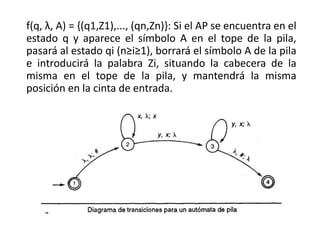
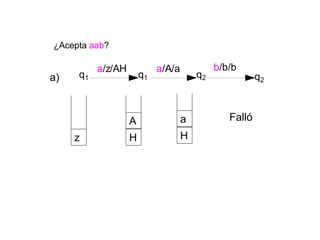
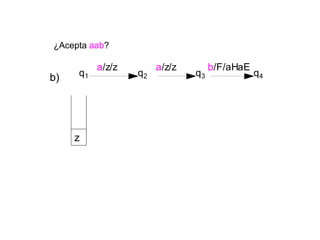
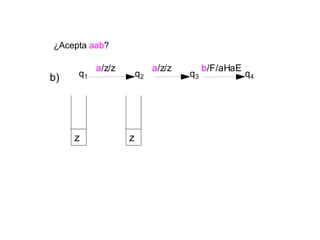
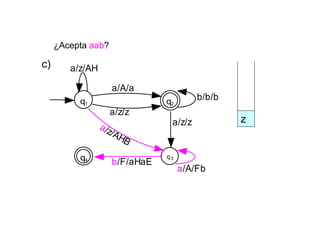
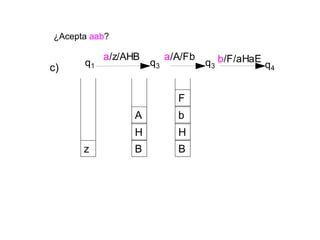
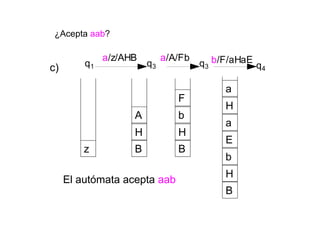
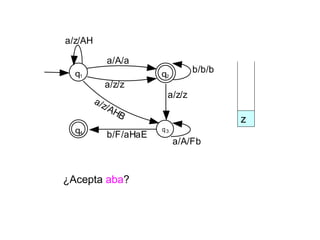
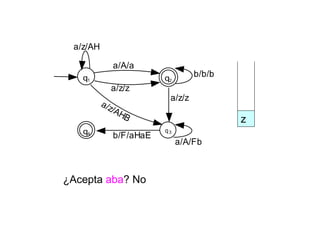
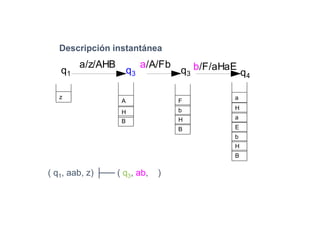
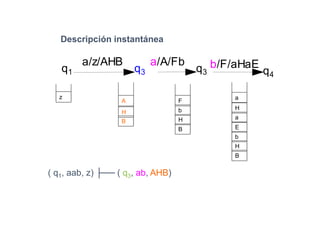
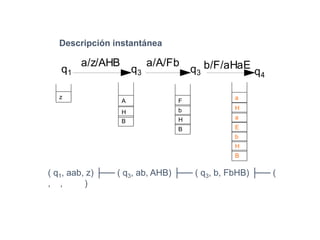
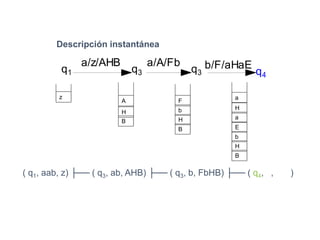
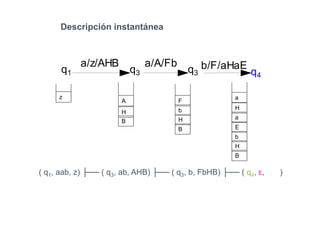
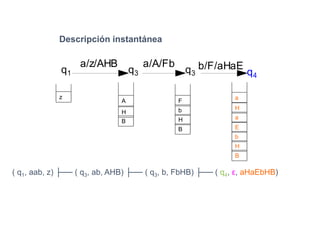
Un autómata de pila es un modelo matemático que analiza cadenas de símbolos y reconoce lenguajes libres de contexto dentro de la jerarquía de Chomsky. Se define formalmente mediante una séptupla que incluye un alfabeto de entrada, un alfabeto de pila, un conjunto de estados y una función de transición. Además, se exploran autómatas de pila deterministas y no deterministas, así como sus aplicaciones en el análisis sintáctico y en el desarrollo de herramientas informáticas.

1. Autómatas de Pila
Jesús E. Carpio 14-0807
Juan A. Ramírez 13-1072

2. Autómata de Pila
• Un autómata de pila es un modelo matemático
de un sistema que recibe una cadena
constituida por símbolos de un alfabeto y
determina si esa cadena pertenece al lenguaje
que el autómata reconoce.
• El lenguaje que reconoce un autómata con pila
pertenece al grupo de los lenguajes libres de
contexto en la clasificación de la Jerarquía de
Chomsky.

3. Definición formal
Un Autómata a Pila se define como la séptupla:(Σ, P, Q, A0, q0,
f, F)donde:
• Σ: alfabeto de entrada.
• P: alfabeto de la pila.
• Q: conjunto de estados.
• A0: símbolo inicial de la pila (#).
• q0: símbolo inicial del conjunto de estados.
• f: función de transición. Es una aplicación de
• Q x Σ {λ} x P en el conjunto de partes de P(QxP)*.
• F: conjunto de estados finales o de aceptación.

4. Diagrama de transición
Un diagrama de transición (Función de transición)
modela el comportamiento del autómata. Es una
aplicación de QxΣ∪{λ}xP en el conjunto de partes de
P(QxP)*.
Pudiendo interpretarlo de la siguiente forma: f(q, a, A)
= {(q1,Z1),…, (qn, Zn)} : Si el AP se en encuentra en el
estado q, lee el símbolo a de la cinta de entrada, y
aparece el símbolo A en el tope de la pila, pasará al
estado qi (n≥i≥1), borrará el símbolo A de la pila e
introducirá la palabra Zi, situando la cabecera de la
misma en el tope de la pila, y avanzando una posición
en la cinta de entrada.

5. f(q, λ, A) = {(q1,Z1),..., (qn,Zn)}: Si el AP se encuentra en el
estado q y aparece el símbolo A en el tope de la pila,
pasará al estado qi (n≥i≥1), borrará el símbolo A de la pila
e introducirá la palabra Zi, situando la cabecera de la
misma en el tope de la pila, y mantendrá la misma
posición en la cinta de entrada.

6. Autómata de Pila Determinista
Un AP es Determinístico si verifica:
1. ∀q∈Q, ∀A∈P, cardinal(f(q, λ, A)) 0⇒f(q, a, A) =∅,
∀a∈Σ.
2. ∀q∈Q,∀A∈P,∀a∈Σ∪{λ} ⇒cardinal(f(q, a, A))<2.

9. Lenguaje aceptado por un
autómata con pila.
Lenguaje aceptado por un AP (M=(Σ, P, Q, A0, q0, f, F)
• Lenguaje aceptado por criterio de estado final
LEF(M) = (x / (q0, x, A0) →* (p, λ, X), p∈F, X∈P*}
• Lenguaje aceptado por criterio de pila vacía
LPV(M) = (x / (q0, x, A0) →* (p, λ, λ), p∈Q}

10. Ejemplo: Autómata con pila que reconoce el lenguaje
L={xnym, n>m}
• Aplicamos el algoritmo de LEF⇒LPV

11. Autómatas finitos con pila no-
deterministas (AFPND)
• Un autómata finito con pila no-determinista
(AFPND) es una séptupla donde:

12. Es decir, el comportamiento del autómata depende en cada transición
• del estado actual
• posiblemente del siguiente símbolo de la entrada
• del símbolo en la cima de la pila
Y se modifica el autómata en el sentido que
• se cambia (posiblemente) del estado
• se consume (posiblemente) el siguiente símbolo de la entrada
• se modifica (posiblemente) el contenido de la cima de la pila.

13. Generalidades
q1 q2
q3q4
a/z/AH
a/A/a
b/b/b
a/z/z
a/A/Fb
b/F/aHaE
a/z/z
a/z/AHB
Quitar Colocar
z
Ejemplo

14. q1 q2
q3q4
a/z/AH
a/A/a
b/b/b
a/z/z
a/A/Fb
b/F/aHaE
a/z/z
a/z/AHB z
¿Acepta aab?

15. ¿Acepta aab?
q1 q2
q3q4
a/z/AH
a/A/a
b/b/b
a/z/z
a/A/Fb
b/F/aHaE
a/z/z
a/z/AHB
z

16. ¿Acepta aab?
a/z/AH a/A/a b/b/b
q2q1 q2
q1
z
a)

17. ¿Acepta aab?
a/z/AH a/A/a b/b/b
q2q1 q2
q1
z
a)
H
A

18. ¿Acepta aab?
a/z/AH a/A/a b/b/b
q2q1 q2
q1
z
a)
H
A
H
a

19. ¿Acepta aab?
a/z/AH a/A/a b/b/b
q2q1 q2
q1
z
a)
H
A
H
a Falló

20. ¿Acepta aab?
q1 q2
q3q4
a/z/AH
a/A/a
b/b/b
a/z/z
a/A/Fb
b/F/aHaE
a/z/z
a/z/AHB
z
b)

21. ¿Acepta aab?
a/z/z a/z/z b/F/aHaE
q3q2 q4q1
z
b)

23. ¿Acepta aab?
a/z/z a/z/z b/F/aHaE
q3q2 q4q1
z
b)
z

24. ¿Acepta aab?
a/z/z a/z/z b/F/aHaE
q3q2 q4q1
z
b)
z z

25. ¿Acepta aab?
a/z/z a/z/z b/F/aHaE
q3q2 q4q1
z
b)
z z
Falló

26. ¿Acepta aab?
q1 q2
q3q4
a/z/AH
a/A/a
b/b/b
a/z/z
a/A/Fb
b/F/aHaE
a/z/z
a/z/AHB
z
c)

27. ¿Acepta aab?
a/z/AHB a/A/Fb b/F/aHaEq3q3 q4
q1
z
c)

28. ¿Acepta aab?
a/z/AHB a/A/Fb b/F/aHaEq3q3 q4
q1
z
c)
B
H
A

29. ¿Acepta aab?
a/z/AHB a/A/Fb b/F/aHaEq3q3 q4
q1
z
c)
B
H
A
B
H
b
F

30. ¿Acepta aab?
a/z/AHB a/A/Fb b/F/aHaEq3q3 q4
q1
z
c)
B
H
A
B
H
b
F
B
H
b
E
a
H
a

31. ¿Acepta aab?
a/z/AHB a/A/Fb b/F/aHaEq3q3 q4
q1
z
c)
B
H
A
B
H
b
F
B
H
b
E
a
H
a
El autómata acepta aab

32. q1 q2
q3q4
a/z/AH
a/A/a
b/b/b
a/z/z
a/A/Fb
b/F/aHaE
a/z/z
a/z/AHB
z
¿Acepta ab?

33. q1 q2
q3q4
a/z/AH
a/A/a
b/b/b
a/z/z
a/A/Fb
b/F/aHaE
a/z/z
a/z/AHB z
¿Acepta ab? No

34. q1 q2
q3q4
a/z/AH
a/A/a
b/b/b
a/z/z
a/A/Fb
b/F/aHaE
a/z/z
a/z/AHB
z
¿Acepta aba?

35. q1 q2
q3q4
a/z/AH
a/A/a
b/b/b
a/z/z
a/A/Fb
b/F/aHaE
a/z/z
a/z/AHB z
¿Acepta aba? No

36. Descripción instantánea
z
B
H
A
B
H
b
F
B
H
b
E
a
H
a
a/z/AHB a/A/Fb b/F/aHaEq3q3 q4
q1
( q1, aab, z)

37. Descripción instantánea
z
B
H
A
B
H
b
F
B
H
b
E
a
H
a
a/z/AHB a/A/Fb b/F/aHaEq3q3 q4
q1
( q1, aab, z) ├── ( , , )

38. Descripción instantánea
z
B
H
A
B
H
b
F
B
H
b
E
a
H
a
a/z/AHB a/A/Fb b/F/aHaEq3q3 q4
q1
( q1, aab, z) ├── ( q3, , )

39. Descripción instantánea
z
B
H
A
B
H
b
F
B
H
b
E
a
H
a
a/z/AHB a/A/Fb b/F/aHaEq3q3 q4
q1
( q1, aab, z) ├── ( q3, ab, )

40. Descripción instantánea
z
B
H
A
B
H
b
F
B
H
b
E
a
H
a
a/z/AHB a/A/Fb b/F/aHaEq3q3 q4
q1
( q1, aab, z) ├── ( q3, ab, AHB)

41. Descripción instantánea
z
B
H
A
B
H
b
F
B
H
b
E
a
H
a
a/z/AHB a/A/Fb b/F/aHaEq3q3 q4
q1
( q1, aab, z) ├── ( q3, ab, AHB) ├── ( , , )

42. Descripción instantánea
z
B
H
A
B
H
b
F
B
H
b
E
a
H
a
a/z/AHB a/A/Fb b/F/aHaEq3q3 q4
q1
( q1, aab, z) ├── ( q3, ab, AHB) ├── ( q3, , )

43. Descripción instantánea
z
B
H
A
B
H
b
F
B
H
b
E
a
H
a
a/z/AHB a/A/Fb b/F/aHaEq3q3 q4
q1
( q1, aab, z) ├── ( q3, ab, AHB) ├── ( q3, b, )

44. Descripción instantánea
z
B
H
A
B
H
b
F
B
H
b
E
a
H
a
a/z/AHB a/A/Fb b/F/aHaEq3q3 q4
q1
( q1, aab, z) ├── ( q3, ab, AHB) ├── ( q3, b, FbHB)

45. Descripción instantánea
z
B
H
A
B
H
b
F
B
H
b
E
a
H
a
a/z/AHB a/A/Fb b/F/aHaEq3q3 q4
q1
( q1, aab, z) ├── ( q3, ab, AHB) ├── ( q3, b, FbHB) ├── (
, , )

46. Descripción instantánea
z
B
H
A
B
H
b
F
B
H
b
E
a
H
a
a/z/AHB a/A/Fb b/F/aHaEq3q3 q4
q1
( q1, aab, z) ├── ( q3, ab, AHB) ├── ( q3, b, FbHB) ├── ( q4, , )

47. Descripción instantánea
z
B
H
A
B
H
b
F
B
H
b
E
a
H
a
a/z/AHB a/A/Fb b/F/aHaEq3q3 q4
q1
( q1, aab, z) ├── ( q3, ab, AHB) ├── ( q3, b, FbHB) ├── ( q4, ε, )

48. Descripción instantánea
z
B
H
A
B
H
b
F
B
H
b
E
a
H
a
a/z/AHB a/A/Fb b/F/aHaEq3q3 q4
q1
( q1, aab, z) ├── ( q3, ab, AHB) ├── ( q3, b, FbHB) ├── ( q4, ε, aHaEbHB)

49. Aplicaciones que requieren análisis
sintáctico
• Compilador para un computador de automatización industrial
• Herramienta de consulta de bases de datos distribuidas
• Creación de un motor de base de datos relacional
• Creación de un motor de base de datos OO (Base de objetos) y su lenguaje
de consulta (OQL)
• Simulador robótico con lenguaje de programación para robots
• Generador de analizador sintáctico (YACC, JAVACC)

51. Referencias
• Autómatas de Pila: Transiciones - Universidad de
Cantabria -
http://www.slideshare.net/rihardjancomartinez/3-7-
transiciones?qid=c05abe18-18f5-4105-889c-
549d052d50a9&v=&b=&from_search=2
• http://www.uhu.es/francisco.moreno/talf/docs/tema
7.pdf
• Dean Kelly, Teoría de Autómatas y lenguajes Formales.