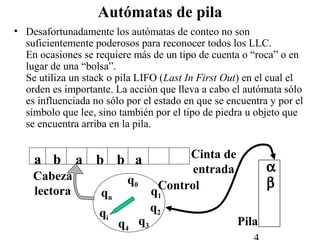
Autómatas de pila (Pushdown automata) son autómatas no deterministas que pueden reconocer lenguajes libres de contexto utilizando una pila LIFO para almacenar información. Los autómatas de pila son más poderosos que los autómatas finitos debido a su capacidad de almacenamiento en pila. Cada transición de un autómata de pila puede leer un símbolo de entrada, sacar un símbolo de la pila y agregar cero o más símbolos a la pila.

1. Autómatas de pila
(Pushdown automata)

2. Autómata de conteo
• Autómata finito determinista con un contador de
enteros o “bolsa” en la que se colocan o extraen
cuentas o “piedras” en respuesta a un símbolo de
entrada. En otras palabras, en cada transición el
autómata no sólo selecciona un nuevo estado sino que
también decide, independientemente del estado de la
bolsa, si añade otra cuenta a la bolsa o saca una cuenta
de la bolsa o la deja igual. La bolsa inicia con una
cuenta y el autómata continúa operando mientras haya
símbolos de entrada y la bolsa no esté vacía. Si se
consumen todos los símbolos de la palabra de entrada
al mismo tiempo que se vacía la bolsa, entonces se
acepta la palabra.

3. Ejemplo: {an
bn
| n ≥ 1}
a
a
b
b
q0
q1 q2

4. Autómatas de pila
• Desafortunadamente los autómatas de conteo no son
suficientemente poderosos para reconocer todos los LLC.
En ocasiones se requiere más de un tipo de cuenta o “roca” o en
lugar de una “bolsa”.
Se utiliza un stack o pila LIFO (Last In First Out) en el cual el
orden es importante. La acción que lleva a cabo el autómata sólo
es influenciada no sólo por el estado en que se encuentra y por el
símbolo que lee, sino también por el tipo de piedra u objeto que
se encuentra arriba en la pila.
a b a b b a
q0
q1
q2
q4
q3
qi
qn
Cinta de
entrada
Cabeza
lectora Control
α
β
Pila

5. Definición formal
• Un autómata de pila (pushdown automata) es una sexteta
(K, Σ, Γ, δ, s0, F) donde:
– K es un conjunto no vacío de estados.
Σ es el alfabeto de entrada, no vacío.
Γ es el alfabeto de la pila, no vacío.
– s0 ∈ K es el estado inicial.
– F ⊂ K es el conjunto de estados finales.
δ ⊂ (K × (Σ ∪ {λ}) × (Γ ∪ {λ})) × (K × Γ*
) es la relación de transición.
(p, u, β) × (q, γ) ∈ δ significa que el autómata está en el estado p, lee el símbolo
u, saca β de la pila, pasa al estado q e introduce γ a la pila.
La operación “push” (sólo meter a la pila) se logra tomando β como la palabra
vacía. La operación “pop” (sólo sacar de la pila) se logra tomando γ como la
palabra vacía.
Ya que δ es una relación y no necesariamente una función, un autómata de pila
es no determinista.
• Una palabra es aceptada por un AP si al “procesarla” completamente, se llega a un
estado final y la pila queda vacía. Debido al no-determinismo del autómata es
posible que al terminar de procesar la palabra, varios estados estén activos. Es
suficiente que uno de estos estados sea final para que la palabra se acepte. L(M)
denota al lenguaje formado por las palabras aceptadas por M.

6. Representación gráfica de un AP
• La transición ((p, u, β), (q, γ)), δ(p, u, β) = (q, γ),
se representa gráficamente por
y significa que cuando estamos en el estado p,
leemos de la palabra de entrada el símbolo u y
sacamos del stack el símbolo β, entonces pasamos
al estado q y ponemos en la pila la cadena γ.
p q
u, β / γ

7. Ejemplo
• Autómata de pila que acepte {ai
bi
| i  0}
– K = {q0, q1}
Σ = {a, b}
Γ = {A}
– s0 = q0
– F = {q0, q1}
δ(q0, a, λ) = (q0, A)
δ(q0, b, A) = (q1, λ)
δ(q1, b, A) = (q1, λ)
a, λ / A b, A / λ
b, A / λq0 q1

8. Ejemplo: palíndromos de longitud impar
• Autómata de pila que acepte {wcwR
| w ∈ {a, b}*
}. wR
es la
palabra w al revés, por ejemplo, “anita”R
= “atina”.
– K = {q0, q1}
Σ = {a, b, c}
Γ = {A, B}
– s0 = q0
– F = {q1}
δ(q0, a, λ) = (q0, A) δ(q1, a, A) = (q1, λ)
δ(q0, b, λ) = (q0, B) δ(q1, b, B) = (q1, λ)
δ(q0, c, λ) = (q1, λ)
a, λ / A
b, λ / B
b, B / λ
a, A / λ
c, λ / λq0 q1

9. Ejemplo: palíndromos de longitud par
• Autómata de pila que acepte {wwR
| w ∈ {a, b}*
}. wR
es la
palabra w al revés, por ejemplo, “anita”R
= “atina”.
– K = {q0, q1}
Σ = {a, b}
Γ = {A, B}
– s0 = q0
– F = {q1}
δ(q0, a, λ) = (q0, A) δ(q1, a, A) = (q1, λ)
δ(q0, b, λ) = (q0, B) δ(q1, b, B) = (q1, λ)
δ(q0, λ, λ) = (q1, λ)
a, λ / A
b, λ / B
b, B / λ
a, A / λ
λ, λ / λq0 q1

10. AF ⊂ AP
• Todo lenguaje aceptado por un autómata finito es
también aceptado por un autómata de pila.
Si M = (K, Σ, δ, s0, F) es un autómata finito,
entonces (K, Σ, Γ, δ’, s0, F) con
Γ = ∅
δ’ = {((p, u, λ), (q, λ)) | (p, u, q) ∈ δ}
acepta el mismo lenguaje que M.
• Los lenguajes libres de contexto son aceptados por
los autómatas de pila y los lenguajes generados
por los autómatas de pila son los lenguajes libres
de contexto.

11. LLC → AP
• Sea G = (V, Σ, R, S) una gramática libre de contexto.
Entonces el autómata de pila M = ({p, q}, Σ, V, δ, p, {q})
donde la relación de transición se define de la siguiente
manera acepta exactamente el mismo lenguaje que G.
– 1) δ(p, λ, λ) = (q, S)
– 2) δ(q, λ, A) = (q, x) para cada regla A → x ∈ R
– 3) δ(q, σ, σ) = (q, λ) para cada σ ∈ Σ
El autómata de pila contiene sólo dos estados. El primero
se utiliza sólo en la primera transición por lo que los
estados no sirven para “recordar” las características de la
palabra de entrada, este “recordatorio” se hace en la pila.
Las transiciones tipo 2) lo que hacen es derivar en la pila
la palabra de entrada sin consumir ningún carácter de
entrada. Las transiciones tipo 3) comparan la palabra en la
pila con la palabra de entrada.

12. Ejemplo
• Obtener un AP que acepte el lenguaje generado por la
gramática libre de contexto cuyas reglas son:
S → aSa S → bSb S → c
• Transiciones del AP
– Tipo 1): δ(p, λ, λ) = (q, S)
– Tipo 2): δ(q, λ, S) = (q, aSa) δ(q, λ, S) = (q, bSb)
δ(q, λ, S) = (q, c)
– Tipo 3): δ(q, a, a) = (q, λ) δ(q, b, b) = (q, λ)
δ(q, c, c) = (q, λ)

13. ...Ejemplo: analizar abcba
Estado Falta leer Pila
p abcba λ
q abcba S
q abcba aSa
q bcba Sa
q bcba bSba
q cba Sba
q cba cba
q ba ba
q a a
q λ λ

14. Cerradura de los LLC
• Dadas dos gramáticas G1 = (V1, Σ1, R1, S1) y G1 = (V2, Σ2, R2, S2)
entonces (se asume, sin perder generalidad, que los símbolos no
terminales de G1 y G2 son disjuntos):
– La gramática libre de contexto que genera L(G1) ∪ L(G2) es
G = (V1 ∪ V2 ∪ {S}, Σ1 ∪ Σ2, R1 ∪ R2 ∪ {S → S1, S → S2}, S)
– La gramática libre de contexto que genera L(G1) L(G2) es
G = (V1 ∪ V2 ∪ {S}, Σ1 ∪ Σ2, R1 ∪ R2 ∪ {S → S1S2}, S)
– La gramática libre de contexto que genera L(G1)*es
G = (V1, Σ1, R1 ∪ {S → λ, S → S1S1}, S}
• Si M1 = (K1, Σ1, Γ1, δ1, s1, F1) y M2 = (K2, Σ2, Γ2, δ2, s2, F2) son dos
autómatas de pila que aceptan los lenguajes L1 y L2,
respectivamente, entonces un autómata de pila que acepta el
lenguaje L1 ∪ L2 es
M1∪2 = (K1∪ K2∪ {s}, Σ1 ∪ Σ2, Γ1 ∪ Γ2,
{((s, λ, λ),(s1, λ)), (s, λ, λ),(s2, λ))} ∪ δ1 ∪ δ2, s, F1 ∪ F2)

15. Ejemplos
• Obtener una GLC para el lenguaje {an
bm
| n ≠ m}.
– {an
bm
| n ≠ m} = {an
bm
| n < m} ∪ {an
bm
| n > m}
– {an
bm
| n < m} es generado por S → aSb, S → Sb, S →
b.
– {an
bm
| n > m} es generado por ........

16. Tarea 5. Primera parte
Fecha límite de entrega: 06/Mayo/2004
• Problema 1.
– Obtener un autómata de pila que acepte el lenguaje
L = {ai
bj
ck
| ¬(i = j = k)}
Utilice el hecho
L = {ai
bj
ck
| ¬(i = j = k)} = {ai
bj
ck
| i ≠ j} ∪ {ai
bj
ck
| j ≠ k}
Sugerencia: para obtener el AP que acepte el primer lenguaje,
primero almacenaría las a’s en la pila para luego ir descontando
una b por cada a en la pila; las a’s deben acabarse antes de
terminar las b’s o deben sobrar a’s al terminar con las b’s; las
c’s no modifican la pila y simplemente se verifica que no haya a
después de la primera b ni que haya a o b después de la primera
c.
La segunda parte de esta Tarea 5 está en la lámina 35 del
TLarchivo09.ppt