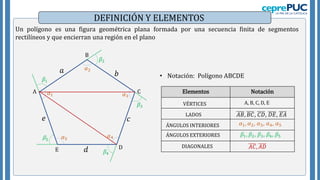
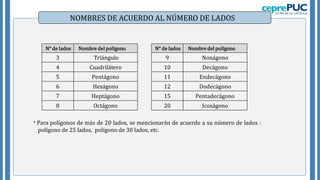
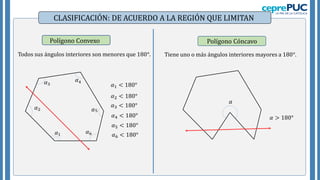
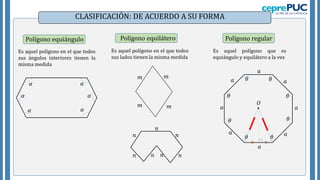
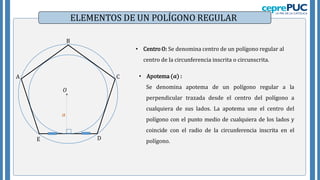
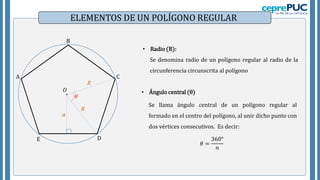
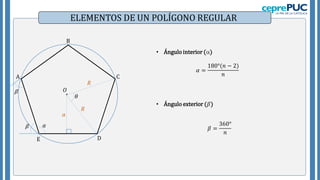
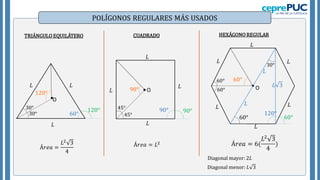
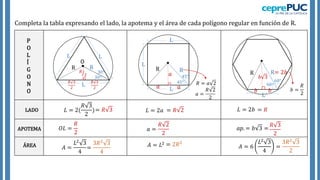
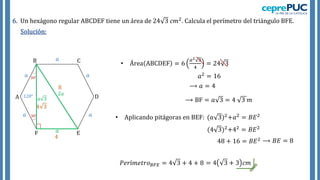
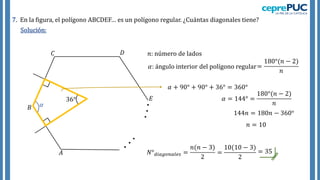
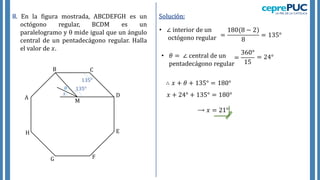
El documento proporciona información sobre polígonos. Define polígonos y sus elementos, y clasifica polígonos de acuerdo a su forma y la región que limitan. También explica polígonos regulares, sus elementos y fórmulas para calcular el área de diferentes polígonos regulares. Incluye ejemplos para practicar el cálculo del área y número de diagonales de polígonos.

1. ¡BIENVENIDOS!
Esta semana revisaremos
los siguientes temas:
POLÍGONOS

2. CONTENIDO DE LA CLASE
 POLÍGONOS
 Definiciones generales de polígonos convexos
 Polígonos regulares
 Ejemplos

3. POLÍGONOS

4. DEFINICIÓN Y ELEMENTOS
Un polígono es una figura geométrica plana formada por una secuencia finita de segmentos
rectilíneos y que encierran una región en el plano
A
B
C
D
E
Elementos Notación
𝛼5
𝛼1
𝛼2
𝛼3
𝛽1
𝛽2
𝛽3
𝛽4
VÉRTICES A, B, C, D, E
LADOS 𝐴𝐵, 𝐵𝐶, 𝐶𝐷, 𝐷𝐸, 𝐸𝐴
ÁNGULOS INTERIORES 𝛼1, 𝛼2, 𝛼3, 𝛼4, 𝛼5
ÁNGULOS EXTERIORES 𝛽1, 𝛽2, 𝛽3, 𝛽4, 𝛽5
DIAGONALES 𝐴𝐶, 𝐴𝐷
𝑎 𝑏
𝑐
𝑑
𝑒
• Notación: Polígono ABCDE

5. NOMBRES DE ACUERDO AL NÚMERO DE LADOS
N° de lados Nombre del polígono
3 Triángulo
4 Cuadrilátero
5 Pentágono
6 Hexágono
7 Heptágono
8 Octágono
* Para polígonos de más de 20 lados, se mencionarán de acuerdo a su número de lados :
polígono de 25 lados, polígono de 30 lados, etc.
N° de lados Nombre del polígono
9 Nonágono
10 Decágono
11 Endecágono
12 Dodecágono
15 Pentadecágono
20 Icoságono

6. CLASIFICACIÓN: DE ACUERDO A LA REGIÓN QUE LIMITAN
Polígono Convexo Polígono Cóncavo
𝛼1
𝛼2
𝛼3
𝛼6
𝛼
Todos sus ángulos interiores son menores que 180°. Tiene uno o más ángulos interiores mayores a 180°.
𝛼1 < 180°
𝛼2 < 180°
𝛼3 < 180°
𝛼4 < 180°
𝛼5 < 180°
𝛼6 < 180°
𝛼 > 180°

7. Polígono equiángulo Polígono regular
Polígono equilátero
𝛼
𝛼
𝛼
𝛼
𝛼
𝛼
Es aquel polígono en el que todos
sus ángulos interiores tienen la
misma medida
Es aquel polígono en el que todos
sus lados tienen la misma medida
Es aquel polígono que es
equiángulo y equilátero a la vez
𝜃
𝜃
𝜃 𝜃
𝜃
𝜃
𝑎
𝑎
𝑎
𝑎
𝑎
𝑎
𝑎
𝑎
𝑂
𝑛
𝑛
𝑛
𝑛
𝑛
𝑛
𝑛
𝑚
𝑚 𝑚
𝑚
CLASIFICACIÓN: DE ACUERDO A SU FORMA

8. PROPIEDADES DE POLÍGONOS CONVEXOS
Si para cierto polígono convexo, “n” es el número de lados, se cumple lo siguiente:
N° de lados = N° de vértices = N° de ángulos interiores = N° de ángulos exteriores = n
Suma de ángulos interiores
Suma de ángulos exteriores
Número de diagonales que
pueden trazarse desde un
vértice
Número total de diagonales
𝑆∡𝑖𝑛𝑡. = 180°(𝑛 − 2)
𝑆∡𝑒𝑥𝑡. = 360°
𝑁°𝐷1𝑉 = 𝑛 − 3
𝑁°𝐷 =
𝑛(𝑛 − 3)
2
Además:
Ejemplo:
Para un nonágono su número de lados es
𝑛 = 9, entonces:
• 𝑆∡𝑖𝑛𝑡. = 180 9 − 2 = 1260°
• 𝑆∡𝑒𝑥𝑡. = 360°
• 𝑁°𝐷1𝑉 = 9 − 3 = 6 𝑑𝑖𝑎𝑔𝑜𝑛𝑎𝑙𝑒𝑠
• 𝑁°𝐷 =
9(9 − 3)
2
= 27 diagonales
1
2
7
6
5 4
3
8
9

9. EJEMPLOS

10. 1. Halla el número total de diagonales que tiene un polígono convexo si se sabe que la suma de sus
ángulos interiores es 2880°.
Solución:
𝑆∡𝑖𝑛𝑡. = 180°(𝑛 − 2)
180° 𝑛 − 2 = 2880°
𝑛 − 2 = 16
𝑛 = 18
𝑁°𝐷 =
𝑛(𝑛 − 3)
2
=
18(18 − 3)
2
=
18(15)
2
= 135 𝑑𝑖𝑎𝑔𝑜𝑛𝑎𝑙𝑒𝑠
n: número de lados

11. Solución:
2. Si el número de lados de un polígono se duplica, el número de sus diagonales se multiplica por 6.
Halla el número de lados del polígono original.
Número de lados Número de diagonales
𝑃𝑜𝑙í𝑔𝑜𝑛𝑜 1
𝑃𝑜𝑙í𝑔𝑜𝑛𝑜 2
𝑁°𝐷 =
𝑛° 𝑙𝑎𝑑𝑜𝑠(𝑛° 𝑙𝑎𝑑𝑜𝑠 − 3)
2
𝑁°𝐷2 = 6(𝑁°𝐷1)
2𝑛(2𝑛 − 3)
2
= 6
𝑛 𝑛 − 3
2
2(2𝑛 − 3) = 6(𝑛 − 3)
4𝑛 − 6 = 6𝑛 − 18
2𝑛 = 12
𝑛 = 6
𝑛 𝐷
2𝑛 6𝐷

12. POLÍGONO REGULAR

13. • Centro O: Se denomina centro de un polígono regular al
centro de la circunferencia inscrita o circunscrita.
ELEMENTOS DE UN POLÍGONO REGULAR
A
B
D
E
C
𝑂
𝑎
• Apotema (𝒂) :
Se denomina apotema de un polígono regular a la
perpendicular trazada desde el centro del polígono a
cualquiera de sus lados. La apotema une el centro del
polígono con el punto medio de cualquiera de los lados y
coincide con el radio de la circunferencia inscrita en el
polígono.

14. A
B
D
E
C
𝑂
𝑎
• Radio (R):
Se denomina radio de un polígono regular al radio de la
circunferencia circunscrita al polígono
• Ángulo central ()
Se llama ángulo central de un polígono regular al
formado en el centro del polígono, al unir dicho punto con
dos vértices consecutivos. Es decir:
𝜃 =
360°
𝑛
𝑅
𝑅
𝜃
ELEMENTOS DE UN POLÍGONO REGULAR

15. A
B
D
E
C
𝑂
𝑎
𝑅
𝑅
𝜃
𝛼 =
180°(𝑛 − 2)
𝑛
• Ángulo interior ()
• Ángulo exterior (𝛽)
𝛽 =
360°
𝑛
𝛼
ELEMENTOS DE UN POLÍGONO REGULAR

16. ÁREA DE UN POLÍGONO REGULAR
𝑅
𝑅
𝑂
𝜃
A
B
D
E
C
𝐿
𝐿
𝐿
𝐿
𝐿
Ejemplo:
Dado el pentágono regular de lado L:
𝑎
Área de un polígono regular = 𝐴 = (𝑝)(𝑎)
Donde:
𝑝: semi perímetro del polígono
𝑎: longitud de la apotema del polígono
Área d𝑒l pentágono = 𝐴 =
5𝐿
2
(𝑎)

17. TRIÁNGULO EQUILÁTERO CUADRADO
60°
120° 90° 90°
90°
30°
30°
45°
45°
120°
O
𝐿
𝐿
𝐿
Á𝑟𝑒𝑎 =
𝐿2 3
4
Á𝑟𝑒𝑎 = 𝐿2
O
𝐿
𝐿
𝐿
𝐿
POLÍGONOS REGULARES MÁS USADOS
HEXÁGONO REGULAR
120°
60°
60°
60°
60° O
𝐿
𝐿
𝐿
𝐿
𝐿
𝐿
𝐿
𝐿
𝐿 3
Á𝑟𝑒𝑎 = 6(
𝐿2 3
4
)
60°
30°
Diagonal mayor: 2𝐿
Diagonal menor: 𝐿 3

18. EJEMPLOS

19. Completa la tabla expresando el lado, la apotema y el área de cada polígono regular en función de R.
R R
R
P
O
L
Í
G
O
N
O
LADO
APOTEMA
ÁREA
30°
30°
L L
R
𝑅
2
𝑅 3
2
𝑅 3
2
O
𝐿 = 2(
𝑅 3
2
)
𝑂𝐿 =
𝑅
2
𝐴 =
𝐿2 3
4
= 𝑅 3
L
L
L
45°
45°
𝑎
𝑎
R
𝑎
𝑅 = 𝑎 2
𝑎 =
𝑅 2
2
𝐿 = 2𝑎 = 𝑅 2
𝑎 =
𝑅 2
2
𝐴 = 𝐿2
60°
L
𝑏
𝑏
𝑏 3
𝐿 = 2𝑏 = 𝑅
𝑎𝑝. = 𝑏 3 =
R= 2𝑏
𝑏 =
𝑅
2
𝐴 = 6
𝐿2 3
4
=
3𝑅2 3
2
𝑅 3
2
=
3𝑅2 3
4
= 2𝑅2

20. 3. Halla el área del triángulo equilátero inscrito en una circunferencia cuyo radio mide 4 cm.
Solución:
4
4
120°
𝑎 𝑎
L
120°
Se cumple que:
𝐿 = 𝑎 3
⟶ 𝐸𝑛 𝑒𝑙 △ 𝑂𝐵𝐶: 𝐿 = 4 3
A
B
C
O
∴ Á𝑟𝑒𝑎 𝐴𝐵𝐶 =
𝐿2 3
4
=
(4 3)2 3
4
= 12 3 𝑐𝑚2
=
(16)(3) 3
4

21. 4. En la figura, 𝐴𝐵𝐶𝐷𝐸𝐹 es un hexágono regular. Si FEMN y EDPQ son cuadrados, calcula el valor de 𝑥.
Solución:
120°
120°
𝐵
𝐶 𝐷
𝑃
𝑂
𝑁
𝑀
𝐴
𝐸
𝐸
𝑥 = 60°
60°
𝑥
𝑥 + 𝑥 + 60° = 180°
2𝑥 = 120°

22. Solución:
5. Calcula el área del triángulo equilátero inscrito en una circunferencia que, a su vez, se halla inscrita
en un cuadrado de 16 𝑚2 de área.
𝑅
𝑅
120°
= 𝑅 3
A
B
C
O O
𝑅
𝑅
2𝑅
2𝑅
Á𝑟𝑒𝑎𝑐𝑢𝑎𝑑𝑟𝑎𝑑𝑜 = (2𝑅)2
16 = 4𝑅2
4 = 𝑅2
R = 2
𝐿 = 𝑅 3 = 2 3
Á𝑟𝑒𝑎𝑡𝑟𝑖á𝑛𝑔𝑢𝑙𝑜 =
𝐿2 3
4
=
(2 3)2 3
4
=
12 3
4
= 3 3 𝑚2

23. 6. Un hexágono regular ABCDEF tiene un área de 24 3 𝑐𝑚2. Calcula el perímetro del triángulo BFE.
Solución:
𝑎
𝑎
𝑎
𝑎
𝑎
𝑎
• Área ABCDEF = 6
𝑎2 3
4
= 24 3
⟶ 𝑎 = 4
120°
𝑎 3
F
A
B C
D
E
• Aplicando pitágoras en BEF: (𝑎 3)2+𝑎2 = 𝐵𝐸2
2𝑎
⟶ BF = 𝑎 3 = 4 3 𝑚
𝑎2 = 16
(4 3)2+42 = 𝐵𝐸2
4 3
4
48 + 16 = 𝐵𝐸2 ⟶ 𝐵𝐸 = 8
8
𝑃𝑒𝑟í𝑚𝑒𝑡𝑟𝑜𝐵𝐹𝐸 = 4 3 + 4 + 8 = 4 3 + 3 𝑐𝑚

24. Solución:
7. En la figura, el polígono ABCDEF… es un polígono regular. ¿Cuántas diagonales tiene?
36°
𝐴
𝐵
𝐶 𝐷
𝐸
𝛼: ángulo interior del polígono regular
𝛼 + 90° + 90° + 36° = 360°
𝛼 = 144° =
180°(𝑛 − 2)
𝑛
144𝑛 = 180𝑛 − 360°
𝑛 = 10
=
180°(𝑛 − 2)
𝑛
𝑛: número de lados
𝑁°𝑑𝑖𝑎𝑔𝑜𝑛𝑎𝑙𝑒𝑠 =
𝑛(𝑛 − 3)
2
=
10(10 − 3)
2
= 35

25. 8. En la figura mostrada, ABCDEFGH es un
octógono regular, BCDM es un
paralelogramo y  mide igual que un ángulo
central de un pentadecágono regular. Halla
el valor de 𝑥.
A
B C
D
E
F
G
H
𝑥
𝜃
Solución:
• ∠ interior de un
octógono regular =
180(8 − 2)
8
= 135°
135°
135°
• 𝜃 = ∠ central de un
pentadecágono regular
=
360°
15
= 24°
∴ 𝑥 + 𝜃 + 135° = 180°
⟶ 𝑥 = 21°
𝑥 + 24° + 135° = 180°
M