Subido porClaseFis120
KEY, PDF215 vistas

Clase 02 - Fis 120

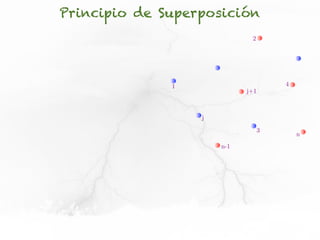
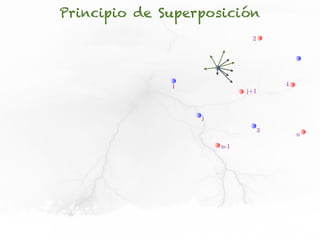
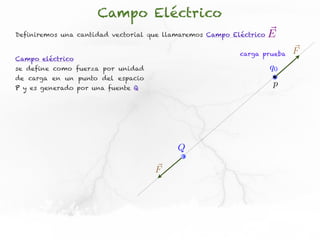
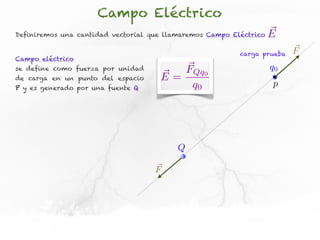
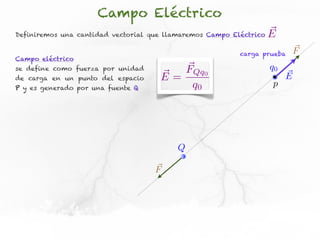
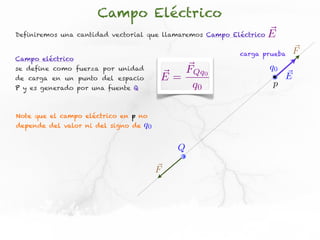
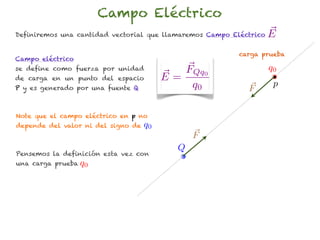
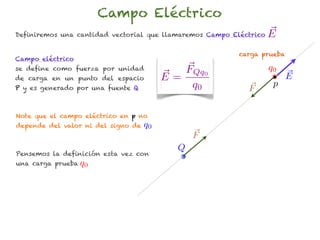
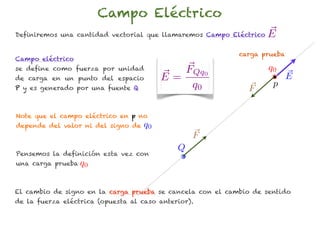
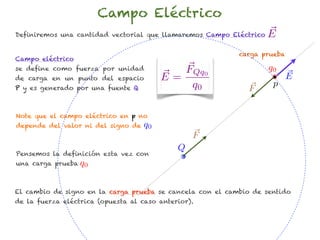
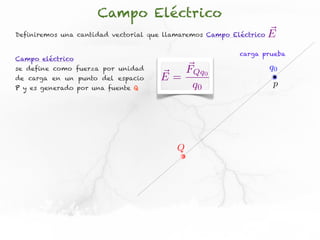
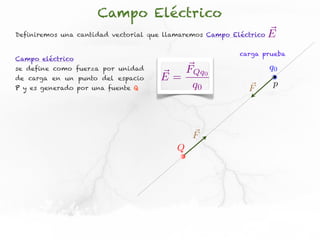
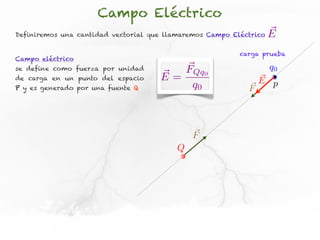
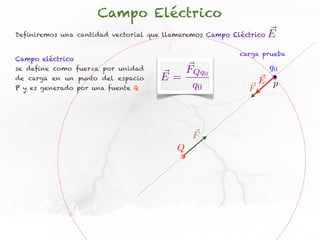
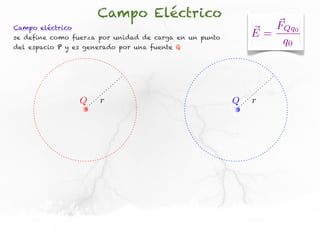
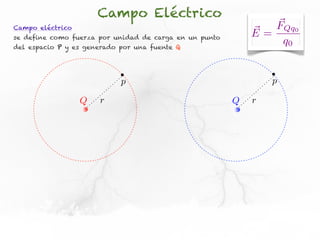
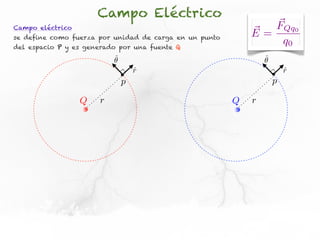
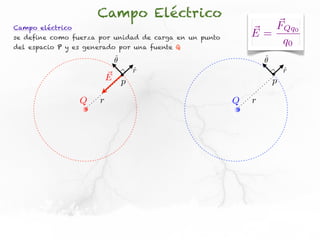
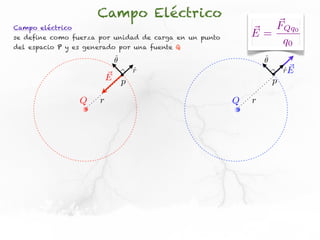
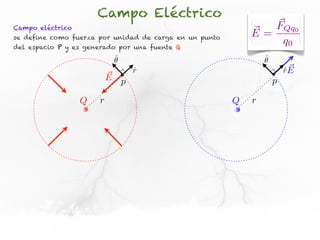
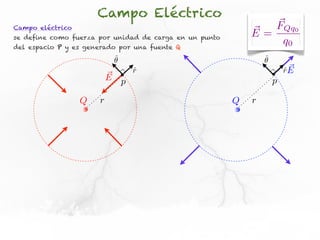
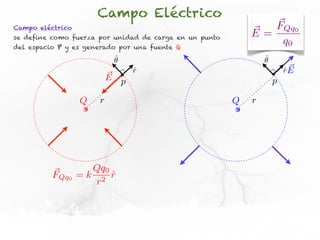
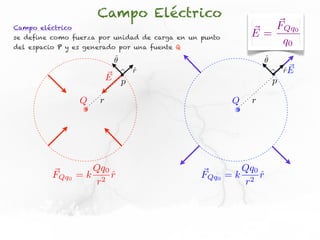
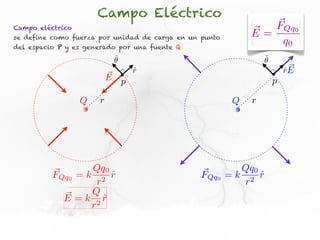
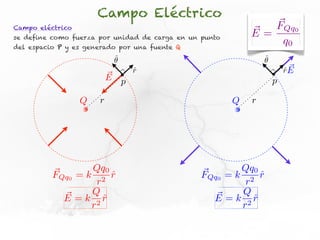
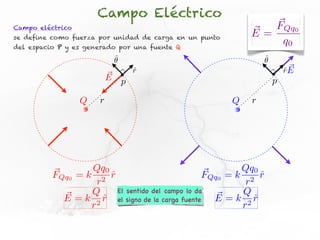
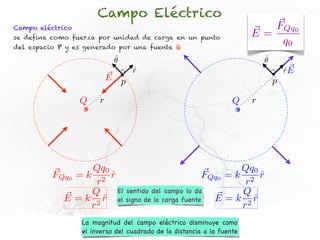
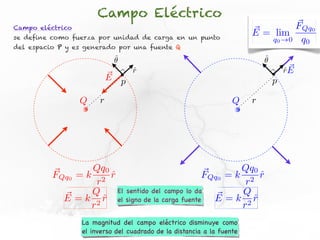
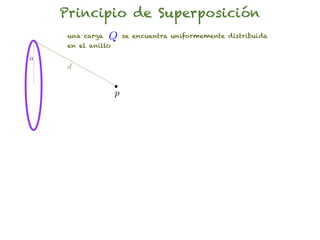
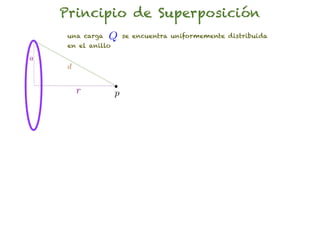
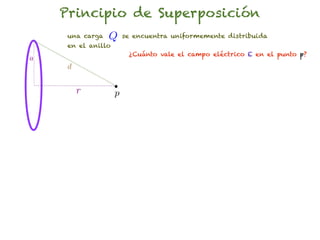
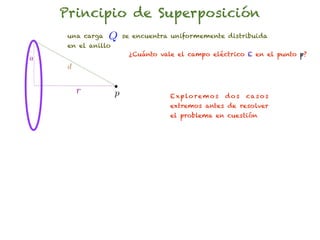
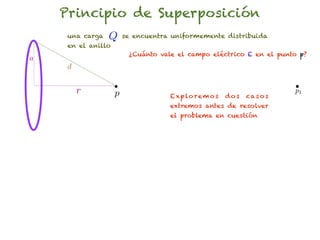
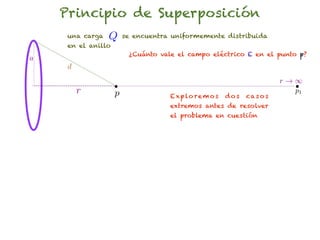
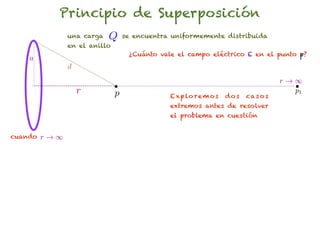
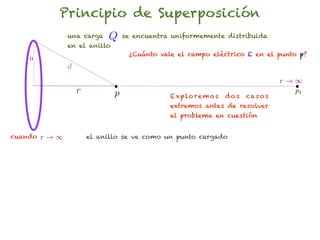
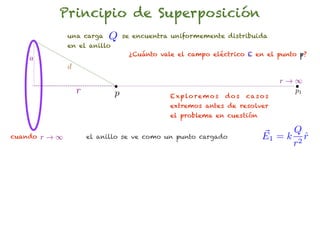
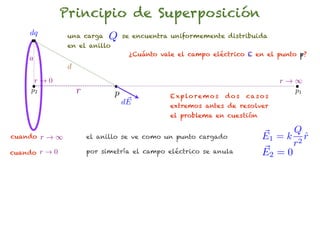
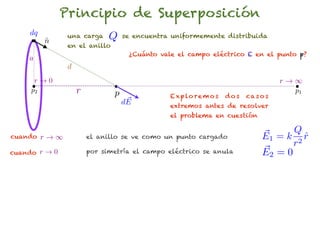
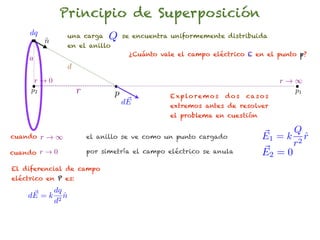
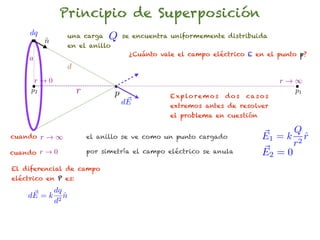
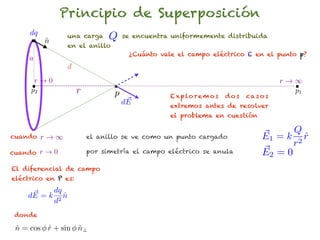
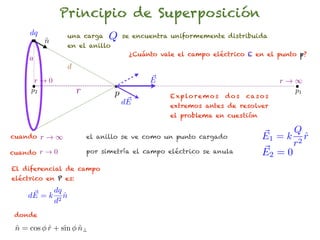
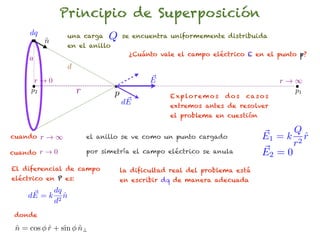
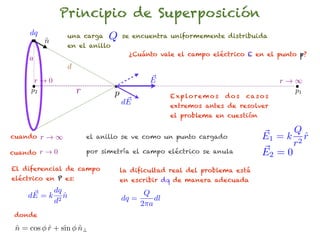
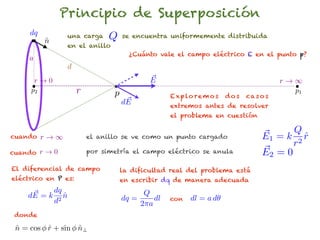
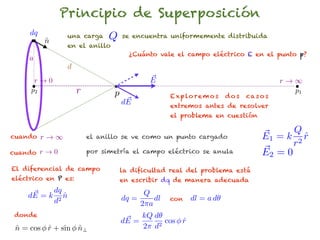
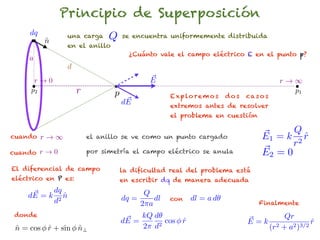
El documento trata sobre el campo eléctrico. Explica que el campo eléctrico en un punto P se define como la fuerza por unidad de carga ejercida en una carga prueba ubicada en P y generada por una fuente de carga Q. Además, señala que el campo eléctrico no depende del valor ni del signo de la carga prueba.

Incrustar presentación

Descargar para leer sin conexión
Física General II Campo Eléctrico, Principio de Superposición Clase 2 Prof. Maximiliano A. Rivera Depto de Física, UTFSM maximiliano.rivera@usm.cl
Principio de Superposición
Principio de Superposición
Principio de Superposición 2 1 4 j+1 j 3 n n-1
Principio de Superposición 2 1 4 j+1 j 3 n n-1
Principio de Superposición 2 n X ~ FN = ~ Fi i=1 1 4 j+1 j 3 n n-1
Principio de Superposición 2 n X ~ FN = ~ Fi i=1 1 4 j+1 ¿Es posible definir un centro de carga en el espíritu que se define un centro de masa? j 3 n n-1
Principio de Superposición 2 n X ~ FN = ~ Fi i=1 1 4 j+1 ¿Es posible definir un centro de carga en el espíritu que se define un centro de masa? j Recuerde que el centro de masa R, se 3 n n X define tal que: M R = ~ m~r i i n-1 i=1
Principio de Superposición 2 n X ~ FN = ~ Fi i=1 1 4 j+1 ¿Es posible definir un centro de carga en el espíritu que se define un centro de masa? j Recuerde que el centro de masa R, se 3 n n X define tal que: M R = ~ m~r i i n-1 i=1 n X con M = mi i=1
Principio de Superposición 2 n X ~ FN = ~ Fi i=1 1 4 j+1 ¿Es posible definir un centro de carga en el espíritu que se define un centro de masa? j Recuerde que el centro de masa R, se 3 n n X define tal que: M R = ~ m~r i i n-1 i=1 n X con M = mi La respuesta es NO, las cargas no son i=1 positivas definidas
Campo Eléctrico
Campo Eléctrico Definiremos una cantidad vectorial que llamaremos Campo Eléctrico E
Campo Eléctrico Definiremos una cantidad vectorial que llamaremos Campo Eléctrico E Campo eléctrico se define como fuerza por unidad de carga en un punto del espacio P y es generado por una fuente Q
Campo Eléctrico Definiremos una cantidad vectorial que llamaremos Campo Eléctrico E Campo eléctrico se define como fuerza por unidad de carga en un punto del espacio P y es generado por una fuente Q Q
Campo Eléctrico Definiremos una cantidad vectorial que llamaremos Campo Eléctrico E Campo eléctrico se define como fuerza por unidad de carga en un punto del espacio P y es generado por una fuente Q p Q
Campo Eléctrico Definiremos una cantidad vectorial que llamaremos Campo Eléctrico E Campo eléctrico se define como fuerza por unidad de carga en un punto del espacio P y es generado por una fuente Q p Q
Campo Eléctrico Definiremos una cantidad vectorial que llamaremos Campo Eléctrico E carga prueba Campo eléctrico se define como fuerza por unidad q0 de carga en un punto del espacio P y es generado por una fuente Q p Q
Campo Eléctrico Definiremos una cantidad vectorial que llamaremos Campo Eléctrico E carga prueba F Campo eléctrico se define como fuerza por unidad q0 de carga en un punto del espacio P y es generado por una fuente Q p Q F
Campo Eléctrico Definiremos una cantidad vectorial que llamaremos Campo Eléctrico E carga prueba F Campo eléctrico se define como fuerza por unidad FQq0 q0 de carga en un punto del espacio E= P y es generado por una fuente Q q0 p Q F
Campo Eléctrico Definiremos una cantidad vectorial que llamaremos Campo Eléctrico E carga prueba F Campo eléctrico se define como fuerza por unidad FQq0 q0 de carga en un punto del espacio E= E P y es generado por una fuente Q q0 p Q F
Campo Eléctrico Definiremos una cantidad vectorial que llamaremos Campo Eléctrico E carga prueba F Campo eléctrico se define como fuerza por unidad FQq0 q0 de carga en un punto del espacio E= E P y es generado por una fuente Q q0 p Note que el campo eléctrico en p no depende del valor ni del signo de q0 Q F
Campo Eléctrico Definiremos una cantidad vectorial que llamaremos Campo Eléctrico E Campo eléctrico se define como fuerza por unidad FQq0 de carga en un punto del espacio E= P y es generado por una fuente Q q0 p Note que el campo eléctrico en p no depende del valor ni del signo de q0 Q
Campo Eléctrico Definiremos una cantidad vectorial que llamaremos Campo Eléctrico E Campo eléctrico se define como fuerza por unidad FQq0 de carga en un punto del espacio E= P y es generado por una fuente Q q0 p Note que el campo eléctrico en p no depende del valor ni del signo de q0 Q Pensemos la definición esta vez con una carga prueba q0
Campo Eléctrico Definiremos una cantidad vectorial que llamaremos Campo Eléctrico E carga prueba Campo eléctrico se define como fuerza por unidad FQq0 q0 de carga en un punto del espacio E= P y es generado por una fuente Q q0 p Note que el campo eléctrico en p no depende del valor ni del signo de q0 Q Pensemos la definición esta vez con una carga prueba q0
Campo Eléctrico Definiremos una cantidad vectorial que llamaremos Campo Eléctrico E carga prueba Campo eléctrico se define como fuerza por unidad FQq0 q0 de carga en un punto del espacio E= P y es generado por una fuente Q q0 p F Note que el campo eléctrico en p no depende del valor ni del signo de q0 F Q Pensemos la definición esta vez con una carga prueba q0
Campo Eléctrico Definiremos una cantidad vectorial que llamaremos Campo Eléctrico E carga prueba Campo eléctrico se define como fuerza por unidad FQq0 q0 de carga en un punto del espacio E= E P y es generado por una fuente Q q0 p F Note que el campo eléctrico en p no depende del valor ni del signo de q0 F Q Pensemos la definición esta vez con una carga prueba q0
Campo Eléctrico Definiremos una cantidad vectorial que llamaremos Campo Eléctrico E carga prueba Campo eléctrico se define como fuerza por unidad FQq0 q0 de carga en un punto del espacio E= E P y es generado por una fuente Q q0 p F Note que el campo eléctrico en p no depende del valor ni del signo de q0 F Q Pensemos la definición esta vez con una carga prueba q0 El cambio de signo en la carga prueba se cancela con el cambio de sentido de la fuerza eléctrica (opuesta al caso anterior).
Campo Eléctrico Definiremos una cantidad vectorial que llamaremos Campo Eléctrico E carga prueba Campo eléctrico se define como fuerza por unidad FQq0 q0 de carga en un punto del espacio E= E P y es generado por una fuente Q q0 p F Note que el campo eléctrico en p no depende del valor ni del signo de q0 F Q Pensemos la definición esta vez con una carga prueba q0 El cambio de signo en la carga prueba se cancela con el cambio de sentido de la fuerza eléctrica (opuesta al caso anterior).
Campo Eléctrico Definiremos una cantidad vectorial que llamaremos Campo Eléctrico E Campo eléctrico se define como fuerza por unidad FQq0 de carga en un punto del espacio E= P y es generado por una fuente Q q0 p Q
Campo Eléctrico Definiremos una cantidad vectorial que llamaremos Campo Eléctrico E carga prueba Campo eléctrico se define como fuerza por unidad FQq0 q0 de carga en un punto del espacio E= P y es generado por una fuente Q q0 p Q
Campo Eléctrico Definiremos una cantidad vectorial que llamaremos Campo Eléctrico E carga prueba Campo eléctrico se define como fuerza por unidad FQq0 q0 de carga en un punto del espacio E= P y es generado por una fuente Q q0 p F F Q
Campo Eléctrico Definiremos una cantidad vectorial que llamaremos Campo Eléctrico E carga prueba Campo eléctrico se define como fuerza por unidad FQq0 q0 de carga en un punto del espacio E= E p P y es generado por una fuente Q q0 F F Q
Campo Eléctrico Definiremos una cantidad vectorial que llamaremos Campo Eléctrico E carga prueba Campo eléctrico se define como fuerza por unidad FQq0 q0 de carga en un punto del espacio E= E p P y es generado por una fuente Q q0 F F Q
Campo Eléctrico Campo eléctrico FQq0 se define como fuerza por unidad de carga en un punto E= del espacio P y es generado por una fuente Q q0 Q Q
Campo Eléctrico Campo eléctrico FQq0 se define como fuerza por unidad de carga en un punto E= del espacio P y es generado por una fuente Q q0 Q r Q r
Campo Eléctrico Campo eléctrico FQq0 se define como fuerza por unidad de carga en un punto E= del espacio P y es generado por una fuente Q q0 Q r Q r
Campo Eléctrico Campo eléctrico FQq0 se define como fuerza por unidad de carga en un punto E= del espacio P y es generado por una fuente Q q0 p p Q r Q r
Campo Eléctrico Campo eléctrico FQq0 se define como fuerza por unidad de carga en un punto E= del espacio P y es generado por una fuente Q q0 ˆ ✓ ˆ ✓ r ˆ r ˆ p p Q r Q r
Campo Eléctrico Campo eléctrico FQq0 se define como fuerza por unidad de carga en un punto E= del espacio P y es generado por una fuente Q q0 ˆ ✓ ˆ ✓ r ˆ r ˆ E p p Q r Q r
Campo Eléctrico Campo eléctrico FQq0 se define como fuerza por unidad de carga en un punto E= del espacio P y es generado por una fuente Q q0 ˆ ✓ ˆ ✓ r ˆ rE ˆ E p p Q r Q r
Campo Eléctrico Campo eléctrico FQq0 se define como fuerza por unidad de carga en un punto E= del espacio P y es generado por una fuente Q q0 ˆ ✓ ˆ ✓ r ˆ rE ˆ E p p Q r Q r
Campo Eléctrico Campo eléctrico FQq0 se define como fuerza por unidad de carga en un punto E= del espacio P y es generado por una fuente Q q0 ˆ ✓ ˆ ✓ r ˆ rE ˆ E p p Q r Q r
Campo Eléctrico Campo eléctrico FQq0 se define como fuerza por unidad de carga en un punto E= del espacio P y es generado por una fuente Q q0 ˆ ✓ ˆ ✓ r ˆ rE ˆ E p p Q r Q r Qq0 FQq0 =k 2 rˆ r
Campo Eléctrico Campo eléctrico FQq0 se define como fuerza por unidad de carga en un punto E= del espacio P y es generado por una fuente Q q0 ˆ ✓ ˆ ✓ r ˆ rE ˆ E p p Q r Q r Qq0 Qq0 FQq0 =k 2 rˆ FQq0 =k 2 rˆ r r
Campo Eléctrico Campo eléctrico FQq0 se define como fuerza por unidad de carga en un punto E= del espacio P y es generado por una fuente Q q0 ˆ ✓ ˆ ✓ r ˆ rE ˆ E p p Q r Q r Qq0 Qq0 FQq0 = k 2 r ˆ FQq0 =k 2 rˆ r r Q E = k 2r ˆ r
Campo Eléctrico Campo eléctrico FQq0 se define como fuerza por unidad de carga en un punto E= del espacio P y es generado por una fuente Q q0 ˆ ✓ ˆ ✓ r ˆ rE ˆ E p p Q r Q r Qq0 Qq0 FQq0 = k 2 r ˆ FQq0 = k 2 r ˆ r r Q Q E = k 2r ˆ E = k 2r ˆ r r
Campo Eléctrico Campo eléctrico FQq0 se define como fuerza por unidad de carga en un punto E= del espacio P y es generado por una fuente Q q0 ˆ ✓ ˆ ✓ r ˆ rE ˆ E p p Q r Q r Qq0 Qq0 FQq0 = k 2 r ˆ FQq0 = k 2 r ˆ r r Q El sentido del campo lo da Q E = k 2 r el signo de la carga fuente E = k 2 r ˆ ˆ r r
Campo Eléctrico Campo eléctrico FQq0 se define como fuerza por unidad de carga en un punto E= del espacio P y es generado por una fuente Q q0 ˆ ✓ ˆ ✓ r ˆ rE ˆ E p p Q r Q r Qq0 Qq0 FQq0 = k 2 r ˆ FQq0 = k 2 r ˆ r r Q El sentido del campo lo da Q E = k 2 r el signo de la carga fuente E = k 2 r ˆ ˆ r r La magnitud del campo eléctrico disminuye como el inverso del cuadrado de la distancia a la fuente
Campo Eléctrico Campo eléctrico FQq0 se define como fuerza por unidad de carga en un punto E = lim q0 !0 q0 del espacio P y es generado por una fuente Q ˆ ✓ ˆ ✓ r ˆ rE ˆ E p p Q r Q r Qq0 Qq0 FQq0 = k 2 r ˆ FQq0 = k 2 r ˆ r r Q El sentido del campo lo da Q E = k 2 r el signo de la carga fuente E = k 2 r ˆ ˆ r r La magnitud del campo eléctrico disminuye como el inverso del cuadrado de la distancia a la fuente
Principio de Superposición d
Principio de Superposición una carga Q se encuentra uniformemente distribuida en el anillo d
Principio de Superposición una carga Q se encuentra uniformemente distribuida en el anillo a d
Principio de Superposición una carga Q se encuentra uniformemente distribuida en el anillo a d p
Principio de Superposición una carga Q se encuentra uniformemente distribuida en el anillo a d r p
Principio de Superposición una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r p
Principio de Superposición una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r p E x p lo r e m o s dos ca s o s extremos antes de resolver el problema en cuestión
Principio de Superposición una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r p E x p lo r e m o s dos ca s o s p1 extremos antes de resolver el problema en cuestión
Principio de Superposición una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!1 r p E x p lo r e m o s dos ca s o s p1 extremos antes de resolver el problema en cuestión
Principio de Superposición una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!1 r p E x p lo r e m o s dos ca s o s p1 extremos antes de resolver el problema en cuestión cuando r!1
Principio de Superposición una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!1 r p E x p lo r e m o s dos ca s o s p1 extremos antes de resolver el problema en cuestión cuando r!1 el anillo se ve como un punto cargado
Principio de Superposición una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!1 r p E x p lo r e m o s dos ca s o s p1 extremos antes de resolver el problema en cuestión Q cuando r!1 el anillo se ve como un punto cargado E1 = k 2 r ˆ r
Principio de Superposición una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!0 r!1 p2 r p E x p lo r e m o s dos ca s o s p1 extremos antes de resolver el problema en cuestión Q cuando r!1 el anillo se ve como un punto cargado E1 = k 2 r ˆ r
Principio de Superposición una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!0 r!1 p2 r p E x p lo r e m o s dos ca s o s p1 extremos antes de resolver el problema en cuestión Q cuando r!1 el anillo se ve como un punto cargado E1 = k 2 r ˆ r cuando r ! 0
Principio de Superposición una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!0 r!1 p2 r p E x p lo r e m o s dos ca s o s p1 extremos antes de resolver el problema en cuestión Q cuando r!1 el anillo se ve como un punto cargado E1 = k 2 r ˆ r cuando r ! 0 por simetría el campo eléctrico se anula
Principio de Superposición una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!0 r!1 p2 r p E x p lo r e m o s dos ca s o s p1 extremos antes de resolver el problema en cuestión Q cuando r!1 el anillo se ve como un punto cargado E1 = k 2 r ˆ r cuando r ! 0 por simetría el campo eléctrico se anula ~ E2 = 0
Principio de Superposición dq una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!0 r!1 p2 r p E x p lo r e m o s dos ca s o s p1 extremos antes de resolver el problema en cuestión Q cuando r!1 el anillo se ve como un punto cargado E1 = k 2 r ˆ r cuando r ! 0 por simetría el campo eléctrico se anula ~ E2 = 0
Principio de Superposición dq una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!0 r!1 p2 r p E x p lo r e m o s dos ca s o s p1 ~ dE extremos antes de resolver el problema en cuestión Q cuando r!1 el anillo se ve como un punto cargado E1 = k 2 r ˆ r cuando r ! 0 por simetría el campo eléctrico se anula ~ E2 = 0
Principio de Superposición dq n ˆ una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!0 r!1 p2 r p E x p lo r e m o s dos ca s o s p1 ~ dE extremos antes de resolver el problema en cuestión Q cuando r!1 el anillo se ve como un punto cargado E1 = k 2 r ˆ r cuando r ! 0 por simetría el campo eléctrico se anula ~ E2 = 0
Principio de Superposición dq n ˆ una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!0 r!1 p2 r p E x p lo r e m o s dos ca s o s p1 ~ dE extremos antes de resolver el problema en cuestión Q cuando r!1 el anillo se ve como un punto cargado E1 = k 2 r ˆ r cuando r ! 0 por simetría el campo eléctrico se anula ~ E2 = 0 El diferencial de campo eléctrico en P es: ~ = k dq n dE ˆ d 2
Principio de Superposición dq n ˆ una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!0 r!1 p2 r p E x p lo r e m o s dos ca s o s p1 ~ dE extremos antes de resolver el problema en cuestión Q cuando r!1 el anillo se ve como un punto cargado E1 = k 2 r ˆ r cuando r ! 0 por simetría el campo eléctrico se anula ~ E2 = 0 El diferencial de campo eléctrico en P es: ~ = k dq n dE ˆ d 2
Principio de Superposición dq n ˆ una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!0 r!1 p2 r p E x p lo r e m o s dos ca s o s p1 ~ dE extremos antes de resolver el problema en cuestión Q cuando r!1 el anillo se ve como un punto cargado E1 = k 2 r ˆ r cuando r ! 0 por simetría el campo eléctrico se anula ~ E2 = 0 El diferencial de campo eléctrico en P es: ~ = k dq n dE ˆ d 2 donde n = cos r + sin n? ˆ ˆ ˆ
Principio de Superposición dq n ˆ una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!0 ~ E r!1 p2 r p E x p lo r e m o s dos ca s o s p1 ~ dE extremos antes de resolver el problema en cuestión Q cuando r!1 el anillo se ve como un punto cargado E1 = k 2 r ˆ r cuando r ! 0 por simetría el campo eléctrico se anula ~ E2 = 0 El diferencial de campo eléctrico en P es: ~ = k dq n dE ˆ d 2 donde n = cos r + sin n? ˆ ˆ ˆ
Principio de Superposición dq n ˆ una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!0 ~ E r!1 p2 r p E x p lo r e m o s dos ca s o s p1 ~ dE extremos antes de resolver el problema en cuestión Q cuando r!1 el anillo se ve como un punto cargado E1 = k 2 r ˆ r cuando r ! 0 por simetría el campo eléctrico se anula ~ E2 = 0 El diferencial de campo la dificultad real del problema está eléctrico en P es: en escribir dq de manera adecuada ~ = k dq n dE ˆ d 2 donde n = cos r + sin n? ˆ ˆ ˆ
Principio de Superposición dq n ˆ una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!0 ~ E r!1 p2 r p E x p lo r e m o s dos ca s o s p1 ~ dE extremos antes de resolver el problema en cuestión Q cuando r!1 el anillo se ve como un punto cargado E1 = k 2 r ˆ r cuando r ! 0 por simetría el campo eléctrico se anula ~ E2 = 0 El diferencial de campo la dificultad real del problema está eléctrico en P es: en escribir dq de manera adecuada ~ = k dq n dE ˆ Q d 2 dq = dl 2⇡a donde n = cos r + sin n? ˆ ˆ ˆ
Principio de Superposición dq n ˆ una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!0 ~ E r!1 p2 r p E x p lo r e m o s dos ca s o s p1 ~ dE extremos antes de resolver el problema en cuestión Q cuando r!1 el anillo se ve como un punto cargado E1 = k 2 r ˆ r cuando r ! 0 por simetría el campo eléctrico se anula ~ E2 = 0 El diferencial de campo la dificultad real del problema está eléctrico en P es: en escribir dq de manera adecuada ~ = k dq n dE ˆ Q d 2 dq = dl con dl = a d✓ 2⇡a donde n = cos r + sin n? ˆ ˆ ˆ
Principio de Superposición dq n ˆ una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!0 ~ E r!1 p2 r p E x p lo r e m o s dos ca s o s p1 ~ dE extremos antes de resolver el problema en cuestión Q cuando r!1 el anillo se ve como un punto cargado E1 = k 2 r ˆ r cuando r ! 0 por simetría el campo eléctrico se anula ~ E2 = 0 El diferencial de campo la dificultad real del problema está eléctrico en P es: en escribir dq de manera adecuada ~ = k dq n dE ˆ Q d 2 dq = dl con dl = a d✓ 2⇡a donde ~ = kQ d✓ cos r dE ˆ 2⇡ d 2 n = cos r + sin n? ˆ ˆ ˆ
Principio de Superposición dq n ˆ una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!0 ~ E r!1 p2 r p E x p lo r e m o s dos ca s o s p1 ~ dE extremos antes de resolver el problema en cuestión Q cuando r!1 el anillo se ve como un punto cargado E1 = k 2 r ˆ r cuando r ! 0 por simetría el campo eléctrico se anula ~ E2 = 0 El diferencial de campo la dificultad real del problema está eléctrico en P es: en escribir dq de manera adecuada ~ = k dq n dE ˆ Q d 2 dq = dl con dl = a d✓ 2⇡a Finalmente donde ~ = kQ d✓ cos r dE ˆ ~ E=k Qr r ˆ 2⇡ d 2 2 + a2 )3/2 n = cos r + sin n? ˆ ˆ ˆ (r
Principio de Superposición una carga Q se encuentra uniformemente distribuida en el plato Calcule el campo eléctrico en el punto P para una distribución de carga superficial p

Más contenido relacionado

DOC
Cap7 b y la 134-153
porSENCICO
 
PDF
Integrales
porLorena Marquez
 
DOC
Cap7 b y la 134-153
por0g4m3
 
PDF
Introduccion fisica agustin
porBrenda Pineda
 
PDF
38827874 capitulo-7-campo-magnetico-y-ley-de-ampere
porGeorrgge
 
PDF
1 Principios De MecáNica CuáNtica
porMARYAND14
 
PDF
Ecuación
porNEWTON HUAMANI CASTRO
 
PDF
Ep1 s
porGuillermo Pereyra
 
Cap7 b y la 134-153
porSENCICO
 
Integrales
porLorena Marquez
 
Cap7 b y la 134-153
por0g4m3
 
Introduccion fisica agustin
porBrenda Pineda
 
38827874 capitulo-7-campo-magnetico-y-ley-de-ampere
porGeorrgge
 
1 Principios De MecáNica CuáNtica
porMARYAND14
 
Ecuación
porNEWTON HUAMANI CASTRO
 
Ep1 s
porGuillermo Pereyra
 

Similar a Clase 02 - Fis 120

PPT
1b 07 electrostática1
porCAL28
 
PPT
Fisica3– e cy t_3+4_camp_pot_gaussunsam
porsgil1950
 
PPT
Resumen electromagnetismo
porÁngel Leonardo Torres
 
PDF
5. Campo eléctrico
porÁlvaro Pascual Sanz
 
PDF
Concepto de campo electrico
porVictor Lobo
 
DOC
Seminario de la semana 2: Campo electrico
porYuri Milachay
 
PDF
CAMPO ELECTRICO
porTorimat Cordova
 
PPT
2f 03 campoelectrostatico
porCAL28
 
PDF
Conceptos campo electrico y carga ley de coulomb
porDiego Moreno Ortiz
 
PDF
2-campo-electrico-2022.pdfdwf3rt5gwfwrfwrfw
porfranciscolerra
 
PDF
Campo_eléctrico-física_3------2024-1.pdf
porValentnTaboada
 
PDF
Fisica Integrada 02 Campo electrico 2021-I.pdf
porCLAUDIOTOMASSALVADOR
 
PDF
Campo eléctrico- Fisica 3 Universidad Nacional de Ingenieria
pordeivisaleluyawtf
 
PDF
Campo Electrico: Física C-ESPOL
porESPOL
 
PPT
Electrostatica
porpnieto81
 
PDF
Interacción electrostática
porquififluna
 
PDF
1º parcial ff isolución
porApoloeXp
 
PDF
Fisica iii practica nº1
porMoisés Galarza Espinoza
 
DOC
1 s312 pvcf 12-18
por0g4m3
 
DOC
1 s312 pvcf 12-18
porkaterin
 
1b 07 electrostática1
porCAL28
 
Fisica3– e cy t_3+4_camp_pot_gaussunsam
porsgil1950
 
Resumen electromagnetismo
porÁngel Leonardo Torres
 
5. Campo eléctrico
porÁlvaro Pascual Sanz
 
Concepto de campo electrico
porVictor Lobo
 
Seminario de la semana 2: Campo electrico
porYuri Milachay
 
CAMPO ELECTRICO
porTorimat Cordova
 
2f 03 campoelectrostatico
porCAL28
 
Conceptos campo electrico y carga ley de coulomb
porDiego Moreno Ortiz
 
2-campo-electrico-2022.pdfdwf3rt5gwfwrfwrfw
porfranciscolerra
 
Campo_eléctrico-física_3------2024-1.pdf
porValentnTaboada
 
Fisica Integrada 02 Campo electrico 2021-I.pdf
porCLAUDIOTOMASSALVADOR
 
Campo eléctrico- Fisica 3 Universidad Nacional de Ingenieria
pordeivisaleluyawtf
 
Campo Electrico: Física C-ESPOL
porESPOL
 
Electrostatica
porpnieto81
 
Interacción electrostática
porquififluna
 
1º parcial ff isolución
porApoloeXp
 
Fisica iii practica nº1
porMoisés Galarza Espinoza
 
1 s312 pvcf 12-18
por0g4m3
 
1 s312 pvcf 12-18
porkaterin
 

Clase 02 - Fis 120

  • 1.
    Física General II CampoEléctrico, Principio de Superposición Clase 2 Prof. Maximiliano A. Rivera Depto de Física, UTFSM maximiliano.rivera@usm.cl
  • 2.
  • 3.
  • 4.
    Principio de Superposición 2 1 4 j+1 j 3 n n-1
  • 5.
    Principio de Superposición 2 1 4 j+1 j 3 n n-1
  • 6.
    Principio de Superposición 2 n X ~ FN = ~ Fi i=1 1 4 j+1 j 3 n n-1
  • 7.
    Principio de Superposición 2 n X ~ FN = ~ Fi i=1 1 4 j+1 ¿Es posible definir un centro de carga en el espíritu que se define un centro de masa? j 3 n n-1
  • 8.
    Principio de Superposición 2 n X ~ FN = ~ Fi i=1 1 4 j+1 ¿Es posible definir un centro de carga en el espíritu que se define un centro de masa? j Recuerde que el centro de masa R, se 3 n n X define tal que: M R = ~ m~r i i n-1 i=1
  • 9.
    Principio de Superposición 2 n X ~ FN = ~ Fi i=1 1 4 j+1 ¿Es posible definir un centro de carga en el espíritu que se define un centro de masa? j Recuerde que el centro de masa R, se 3 n n X define tal que: M R = ~ m~r i i n-1 i=1 n X con M = mi i=1
  • 10.
    Principio de Superposición 2 n X ~ FN = ~ Fi i=1 1 4 j+1 ¿Es posible definir un centro de carga en el espíritu que se define un centro de masa? j Recuerde que el centro de masa R, se 3 n n X define tal que: M R = ~ m~r i i n-1 i=1 n X con M = mi La respuesta es NO, las cargas no son i=1 positivas definidas
  • 11.
  • 12.
    Campo Eléctrico Definiremos unacantidad vectorial que llamaremos Campo Eléctrico E
  • 13.
    Campo Eléctrico Definiremos unacantidad vectorial que llamaremos Campo Eléctrico E Campo eléctrico se define como fuerza por unidad de carga en un punto del espacio P y es generado por una fuente Q
  • 14.
    Campo Eléctrico Definiremos unacantidad vectorial que llamaremos Campo Eléctrico E Campo eléctrico se define como fuerza por unidad de carga en un punto del espacio P y es generado por una fuente Q Q
  • 15.
    Campo Eléctrico Definiremos unacantidad vectorial que llamaremos Campo Eléctrico E Campo eléctrico se define como fuerza por unidad de carga en un punto del espacio P y es generado por una fuente Q p Q
  • 16.
    Campo Eléctrico Definiremos unacantidad vectorial que llamaremos Campo Eléctrico E Campo eléctrico se define como fuerza por unidad de carga en un punto del espacio P y es generado por una fuente Q p Q
  • 17.
    Campo Eléctrico Definiremos unacantidad vectorial que llamaremos Campo Eléctrico E carga prueba Campo eléctrico se define como fuerza por unidad q0 de carga en un punto del espacio P y es generado por una fuente Q p Q
  • 18.
    Campo Eléctrico Definiremos unacantidad vectorial que llamaremos Campo Eléctrico E carga prueba F Campo eléctrico se define como fuerza por unidad q0 de carga en un punto del espacio P y es generado por una fuente Q p Q F
  • 19.
    Campo Eléctrico Definiremos unacantidad vectorial que llamaremos Campo Eléctrico E carga prueba F Campo eléctrico se define como fuerza por unidad FQq0 q0 de carga en un punto del espacio E= P y es generado por una fuente Q q0 p Q F
  • 20.
    Campo Eléctrico Definiremos unacantidad vectorial que llamaremos Campo Eléctrico E carga prueba F Campo eléctrico se define como fuerza por unidad FQq0 q0 de carga en un punto del espacio E= E P y es generado por una fuente Q q0 p Q F
  • 21.
    Campo Eléctrico Definiremos unacantidad vectorial que llamaremos Campo Eléctrico E carga prueba F Campo eléctrico se define como fuerza por unidad FQq0 q0 de carga en un punto del espacio E= E P y es generado por una fuente Q q0 p Note que el campo eléctrico en p no depende del valor ni del signo de q0 Q F
  • 22.
    Campo Eléctrico Definiremos unacantidad vectorial que llamaremos Campo Eléctrico E Campo eléctrico se define como fuerza por unidad FQq0 de carga en un punto del espacio E= P y es generado por una fuente Q q0 p Note que el campo eléctrico en p no depende del valor ni del signo de q0 Q
  • 23.
    Campo Eléctrico Definiremos unacantidad vectorial que llamaremos Campo Eléctrico E Campo eléctrico se define como fuerza por unidad FQq0 de carga en un punto del espacio E= P y es generado por una fuente Q q0 p Note que el campo eléctrico en p no depende del valor ni del signo de q0 Q Pensemos la definición esta vez con una carga prueba q0
  • 24.
    Campo Eléctrico Definiremos unacantidad vectorial que llamaremos Campo Eléctrico E carga prueba Campo eléctrico se define como fuerza por unidad FQq0 q0 de carga en un punto del espacio E= P y es generado por una fuente Q q0 p Note que el campo eléctrico en p no depende del valor ni del signo de q0 Q Pensemos la definición esta vez con una carga prueba q0
  • 25.
    Campo Eléctrico Definiremos unacantidad vectorial que llamaremos Campo Eléctrico E carga prueba Campo eléctrico se define como fuerza por unidad FQq0 q0 de carga en un punto del espacio E= P y es generado por una fuente Q q0 p F Note que el campo eléctrico en p no depende del valor ni del signo de q0 F Q Pensemos la definición esta vez con una carga prueba q0
  • 26.
    Campo Eléctrico Definiremos unacantidad vectorial que llamaremos Campo Eléctrico E carga prueba Campo eléctrico se define como fuerza por unidad FQq0 q0 de carga en un punto del espacio E= E P y es generado por una fuente Q q0 p F Note que el campo eléctrico en p no depende del valor ni del signo de q0 F Q Pensemos la definición esta vez con una carga prueba q0
  • 27.
    Campo Eléctrico Definiremos unacantidad vectorial que llamaremos Campo Eléctrico E carga prueba Campo eléctrico se define como fuerza por unidad FQq0 q0 de carga en un punto del espacio E= E P y es generado por una fuente Q q0 p F Note que el campo eléctrico en p no depende del valor ni del signo de q0 F Q Pensemos la definición esta vez con una carga prueba q0 El cambio de signo en la carga prueba se cancela con el cambio de sentido de la fuerza eléctrica (opuesta al caso anterior).
  • 28.
    Campo Eléctrico Definiremos unacantidad vectorial que llamaremos Campo Eléctrico E carga prueba Campo eléctrico se define como fuerza por unidad FQq0 q0 de carga en un punto del espacio E= E P y es generado por una fuente Q q0 p F Note que el campo eléctrico en p no depende del valor ni del signo de q0 F Q Pensemos la definición esta vez con una carga prueba q0 El cambio de signo en la carga prueba se cancela con el cambio de sentido de la fuerza eléctrica (opuesta al caso anterior).
  • 29.
    Campo Eléctrico Definiremos unacantidad vectorial que llamaremos Campo Eléctrico E Campo eléctrico se define como fuerza por unidad FQq0 de carga en un punto del espacio E= P y es generado por una fuente Q q0 p Q
  • 30.
    Campo Eléctrico Definiremos unacantidad vectorial que llamaremos Campo Eléctrico E carga prueba Campo eléctrico se define como fuerza por unidad FQq0 q0 de carga en un punto del espacio E= P y es generado por una fuente Q q0 p Q
  • 31.
    Campo Eléctrico Definiremos unacantidad vectorial que llamaremos Campo Eléctrico E carga prueba Campo eléctrico se define como fuerza por unidad FQq0 q0 de carga en un punto del espacio E= P y es generado por una fuente Q q0 p F F Q
  • 32.
    Campo Eléctrico Definiremos unacantidad vectorial que llamaremos Campo Eléctrico E carga prueba Campo eléctrico se define como fuerza por unidad FQq0 q0 de carga en un punto del espacio E= E p P y es generado por una fuente Q q0 F F Q
  • 33.
    Campo Eléctrico Definiremos unacantidad vectorial que llamaremos Campo Eléctrico E carga prueba Campo eléctrico se define como fuerza por unidad FQq0 q0 de carga en un punto del espacio E= E p P y es generado por una fuente Q q0 F F Q
  • 34.
    Campo Eléctrico Campo eléctrico FQq0 se define como fuerza por unidad de carga en un punto E= del espacio P y es generado por una fuente Q q0 Q Q
  • 35.
    Campo Eléctrico Campo eléctrico FQq0 se define como fuerza por unidad de carga en un punto E= del espacio P y es generado por una fuente Q q0 Q r Q r
  • 36.
    Campo Eléctrico Campo eléctrico FQq0 se define como fuerza por unidad de carga en un punto E= del espacio P y es generado por una fuente Q q0 Q r Q r
  • 37.
    Campo Eléctrico Campo eléctrico FQq0 se define como fuerza por unidad de carga en un punto E= del espacio P y es generado por una fuente Q q0 p p Q r Q r
  • 38.
    Campo Eléctrico Campo eléctrico FQq0 se define como fuerza por unidad de carga en un punto E= del espacio P y es generado por una fuente Q q0 ˆ ✓ ˆ ✓ r ˆ r ˆ p p Q r Q r
  • 39.
    Campo Eléctrico Campo eléctrico FQq0 se define como fuerza por unidad de carga en un punto E= del espacio P y es generado por una fuente Q q0 ˆ ✓ ˆ ✓ r ˆ r ˆ E p p Q r Q r
  • 40.
    Campo Eléctrico Campo eléctrico FQq0 se define como fuerza por unidad de carga en un punto E= del espacio P y es generado por una fuente Q q0 ˆ ✓ ˆ ✓ r ˆ rE ˆ E p p Q r Q r
  • 41.
    Campo Eléctrico Campo eléctrico FQq0 se define como fuerza por unidad de carga en un punto E= del espacio P y es generado por una fuente Q q0 ˆ ✓ ˆ ✓ r ˆ rE ˆ E p p Q r Q r
  • 42.
    Campo Eléctrico Campo eléctrico FQq0 se define como fuerza por unidad de carga en un punto E= del espacio P y es generado por una fuente Q q0 ˆ ✓ ˆ ✓ r ˆ rE ˆ E p p Q r Q r
  • 43.
    Campo Eléctrico Campo eléctrico FQq0 se define como fuerza por unidad de carga en un punto E= del espacio P y es generado por una fuente Q q0 ˆ ✓ ˆ ✓ r ˆ rE ˆ E p p Q r Q r Qq0 FQq0 =k 2 rˆ r
  • 44.
    Campo Eléctrico Campo eléctrico FQq0 se define como fuerza por unidad de carga en un punto E= del espacio P y es generado por una fuente Q q0 ˆ ✓ ˆ ✓ r ˆ rE ˆ E p p Q r Q r Qq0 Qq0 FQq0 =k 2 rˆ FQq0 =k 2 rˆ r r
  • 45.
    Campo Eléctrico Campo eléctrico FQq0 se define como fuerza por unidad de carga en un punto E= del espacio P y es generado por una fuente Q q0 ˆ ✓ ˆ ✓ r ˆ rE ˆ E p p Q r Q r Qq0 Qq0 FQq0 = k 2 r ˆ FQq0 =k 2 rˆ r r Q E = k 2r ˆ r
  • 46.
    Campo Eléctrico Campo eléctrico FQq0 se define como fuerza por unidad de carga en un punto E= del espacio P y es generado por una fuente Q q0 ˆ ✓ ˆ ✓ r ˆ rE ˆ E p p Q r Q r Qq0 Qq0 FQq0 = k 2 r ˆ FQq0 = k 2 r ˆ r r Q Q E = k 2r ˆ E = k 2r ˆ r r
  • 47.
    Campo Eléctrico Campo eléctrico FQq0 se define como fuerza por unidad de carga en un punto E= del espacio P y es generado por una fuente Q q0 ˆ ✓ ˆ ✓ r ˆ rE ˆ E p p Q r Q r Qq0 Qq0 FQq0 = k 2 r ˆ FQq0 = k 2 r ˆ r r Q El sentido del campo lo da Q E = k 2 r el signo de la carga fuente E = k 2 r ˆ ˆ r r
  • 48.
    Campo Eléctrico Campo eléctrico FQq0 se define como fuerza por unidad de carga en un punto E= del espacio P y es generado por una fuente Q q0 ˆ ✓ ˆ ✓ r ˆ rE ˆ E p p Q r Q r Qq0 Qq0 FQq0 = k 2 r ˆ FQq0 = k 2 r ˆ r r Q El sentido del campo lo da Q E = k 2 r el signo de la carga fuente E = k 2 r ˆ ˆ r r La magnitud del campo eléctrico disminuye como el inverso del cuadrado de la distancia a la fuente
  • 49.
    Campo Eléctrico Campo eléctrico FQq0 se define como fuerza por unidad de carga en un punto E = lim q0 !0 q0 del espacio P y es generado por una fuente Q ˆ ✓ ˆ ✓ r ˆ rE ˆ E p p Q r Q r Qq0 Qq0 FQq0 = k 2 r ˆ FQq0 = k 2 r ˆ r r Q El sentido del campo lo da Q E = k 2 r el signo de la carga fuente E = k 2 r ˆ ˆ r r La magnitud del campo eléctrico disminuye como el inverso del cuadrado de la distancia a la fuente
  • 50.
  • 51.
    Principio de Superposición una carga Q se encuentra uniformemente distribuida en el anillo d
  • 52.
    Principio de Superposición una carga Q se encuentra uniformemente distribuida en el anillo a d
  • 53.
    Principio de Superposición una carga Q se encuentra uniformemente distribuida en el anillo a d p
  • 54.
    Principio de Superposición una carga Q se encuentra uniformemente distribuida en el anillo a d r p
  • 55.
    Principio de Superposición una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r p
  • 56.
    Principio de Superposición una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r p E x p lo r e m o s dos ca s o s extremos antes de resolver el problema en cuestión
  • 57.
    Principio de Superposición una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r p E x p lo r e m o s dos ca s o s p1 extremos antes de resolver el problema en cuestión
  • 58.
    Principio de Superposición una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!1 r p E x p lo r e m o s dos ca s o s p1 extremos antes de resolver el problema en cuestión
  • 59.
    Principio de Superposición una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!1 r p E x p lo r e m o s dos ca s o s p1 extremos antes de resolver el problema en cuestión cuando r!1
  • 60.
    Principio de Superposición una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!1 r p E x p lo r e m o s dos ca s o s p1 extremos antes de resolver el problema en cuestión cuando r!1 el anillo se ve como un punto cargado
  • 61.
    Principio de Superposición una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!1 r p E x p lo r e m o s dos ca s o s p1 extremos antes de resolver el problema en cuestión Q cuando r!1 el anillo se ve como un punto cargado E1 = k 2 r ˆ r
  • 62.
    Principio de Superposición una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!0 r!1 p2 r p E x p lo r e m o s dos ca s o s p1 extremos antes de resolver el problema en cuestión Q cuando r!1 el anillo se ve como un punto cargado E1 = k 2 r ˆ r
  • 63.
    Principio de Superposición una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!0 r!1 p2 r p E x p lo r e m o s dos ca s o s p1 extremos antes de resolver el problema en cuestión Q cuando r!1 el anillo se ve como un punto cargado E1 = k 2 r ˆ r cuando r ! 0
  • 64.
    Principio de Superposición una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!0 r!1 p2 r p E x p lo r e m o s dos ca s o s p1 extremos antes de resolver el problema en cuestión Q cuando r!1 el anillo se ve como un punto cargado E1 = k 2 r ˆ r cuando r ! 0 por simetría el campo eléctrico se anula
  • 65.
    Principio de Superposición una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!0 r!1 p2 r p E x p lo r e m o s dos ca s o s p1 extremos antes de resolver el problema en cuestión Q cuando r!1 el anillo se ve como un punto cargado E1 = k 2 r ˆ r cuando r ! 0 por simetría el campo eléctrico se anula ~ E2 = 0
  • 66.
    Principio de Superposición dq una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!0 r!1 p2 r p E x p lo r e m o s dos ca s o s p1 extremos antes de resolver el problema en cuestión Q cuando r!1 el anillo se ve como un punto cargado E1 = k 2 r ˆ r cuando r ! 0 por simetría el campo eléctrico se anula ~ E2 = 0
  • 67.
    Principio de Superposición dq una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!0 r!1 p2 r p E x p lo r e m o s dos ca s o s p1 ~ dE extremos antes de resolver el problema en cuestión Q cuando r!1 el anillo se ve como un punto cargado E1 = k 2 r ˆ r cuando r ! 0 por simetría el campo eléctrico se anula ~ E2 = 0
  • 68.
    Principio de Superposición dq n ˆ una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!0 r!1 p2 r p E x p lo r e m o s dos ca s o s p1 ~ dE extremos antes de resolver el problema en cuestión Q cuando r!1 el anillo se ve como un punto cargado E1 = k 2 r ˆ r cuando r ! 0 por simetría el campo eléctrico se anula ~ E2 = 0
  • 69.
    Principio de Superposición dq n ˆ una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!0 r!1 p2 r p E x p lo r e m o s dos ca s o s p1 ~ dE extremos antes de resolver el problema en cuestión Q cuando r!1 el anillo se ve como un punto cargado E1 = k 2 r ˆ r cuando r ! 0 por simetría el campo eléctrico se anula ~ E2 = 0 El diferencial de campo eléctrico en P es: ~ = k dq n dE ˆ d 2
  • 70.
    Principio de Superposición dq n ˆ una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!0 r!1 p2 r p E x p lo r e m o s dos ca s o s p1 ~ dE extremos antes de resolver el problema en cuestión Q cuando r!1 el anillo se ve como un punto cargado E1 = k 2 r ˆ r cuando r ! 0 por simetría el campo eléctrico se anula ~ E2 = 0 El diferencial de campo eléctrico en P es: ~ = k dq n dE ˆ d 2
  • 71.
    Principio de Superposición dq n ˆ una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!0 r!1 p2 r p E x p lo r e m o s dos ca s o s p1 ~ dE extremos antes de resolver el problema en cuestión Q cuando r!1 el anillo se ve como un punto cargado E1 = k 2 r ˆ r cuando r ! 0 por simetría el campo eléctrico se anula ~ E2 = 0 El diferencial de campo eléctrico en P es: ~ = k dq n dE ˆ d 2 donde n = cos r + sin n? ˆ ˆ ˆ
  • 72.
    Principio de Superposición dq n ˆ una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!0 ~ E r!1 p2 r p E x p lo r e m o s dos ca s o s p1 ~ dE extremos antes de resolver el problema en cuestión Q cuando r!1 el anillo se ve como un punto cargado E1 = k 2 r ˆ r cuando r ! 0 por simetría el campo eléctrico se anula ~ E2 = 0 El diferencial de campo eléctrico en P es: ~ = k dq n dE ˆ d 2 donde n = cos r + sin n? ˆ ˆ ˆ
  • 73.
    Principio de Superposición dq n ˆ una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!0 ~ E r!1 p2 r p E x p lo r e m o s dos ca s o s p1 ~ dE extremos antes de resolver el problema en cuestión Q cuando r!1 el anillo se ve como un punto cargado E1 = k 2 r ˆ r cuando r ! 0 por simetría el campo eléctrico se anula ~ E2 = 0 El diferencial de campo la dificultad real del problema está eléctrico en P es: en escribir dq de manera adecuada ~ = k dq n dE ˆ d 2 donde n = cos r + sin n? ˆ ˆ ˆ
  • 74.
    Principio de Superposición dq n ˆ una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!0 ~ E r!1 p2 r p E x p lo r e m o s dos ca s o s p1 ~ dE extremos antes de resolver el problema en cuestión Q cuando r!1 el anillo se ve como un punto cargado E1 = k 2 r ˆ r cuando r ! 0 por simetría el campo eléctrico se anula ~ E2 = 0 El diferencial de campo la dificultad real del problema está eléctrico en P es: en escribir dq de manera adecuada ~ = k dq n dE ˆ Q d 2 dq = dl 2⇡a donde n = cos r + sin n? ˆ ˆ ˆ
  • 75.
    Principio de Superposición dq n ˆ una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!0 ~ E r!1 p2 r p E x p lo r e m o s dos ca s o s p1 ~ dE extremos antes de resolver el problema en cuestión Q cuando r!1 el anillo se ve como un punto cargado E1 = k 2 r ˆ r cuando r ! 0 por simetría el campo eléctrico se anula ~ E2 = 0 El diferencial de campo la dificultad real del problema está eléctrico en P es: en escribir dq de manera adecuada ~ = k dq n dE ˆ Q d 2 dq = dl con dl = a d✓ 2⇡a donde n = cos r + sin n? ˆ ˆ ˆ
  • 76.
    Principio de Superposición dq n ˆ una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!0 ~ E r!1 p2 r p E x p lo r e m o s dos ca s o s p1 ~ dE extremos antes de resolver el problema en cuestión Q cuando r!1 el anillo se ve como un punto cargado E1 = k 2 r ˆ r cuando r ! 0 por simetría el campo eléctrico se anula ~ E2 = 0 El diferencial de campo la dificultad real del problema está eléctrico en P es: en escribir dq de manera adecuada ~ = k dq n dE ˆ Q d 2 dq = dl con dl = a d✓ 2⇡a donde ~ = kQ d✓ cos r dE ˆ 2⇡ d 2 n = cos r + sin n? ˆ ˆ ˆ
  • 77.
    Principio de Superposición dq n ˆ una carga Q se encuentra uniformemente distribuida en el anillo ¿Cuánto vale el campo eléctrico E en el punto p? a d r!0 ~ E r!1 p2 r p E x p lo r e m o s dos ca s o s p1 ~ dE extremos antes de resolver el problema en cuestión Q cuando r!1 el anillo se ve como un punto cargado E1 = k 2 r ˆ r cuando r ! 0 por simetría el campo eléctrico se anula ~ E2 = 0 El diferencial de campo la dificultad real del problema está eléctrico en P es: en escribir dq de manera adecuada ~ = k dq n dE ˆ Q d 2 dq = dl con dl = a d✓ 2⇡a Finalmente donde ~ = kQ d✓ cos r dE ˆ ~ E=k Qr r ˆ 2⇡ d 2 2 + a2 )3/2 n = cos r + sin n? ˆ ˆ ˆ (r
  • 78.
    Principio de Superposición unacarga Q se encuentra uniformemente distribuida en el plato Calcule el campo eléctrico en el punto P para una distribución de carga superficial p

Notas del editor