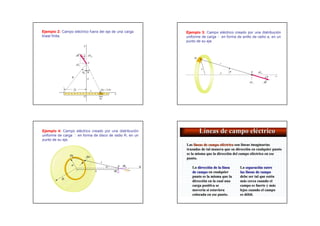
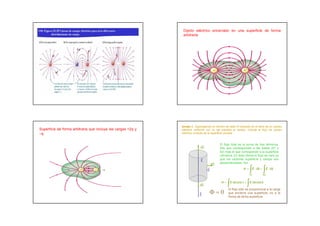
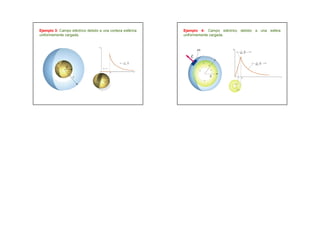
La carga eléctrica es una propiedad fundamental responsable de la interacción electromagnética. Se mide en coulombs y siempre se presenta en múltiplos enteros de la carga del electrón. La Ley de Coulomb establece que las cargas ejercen fuerzas atractivas o repulsivas dependiendo de su signo, variando inversamente con el cuadrado de la distancia. La Ley de Gauss relaciona el flujo del campo eléctrico a través de una superficie cerrada con la carga neta encerrada.

1. CARGA ELÉCTRICA
ELÉ
Características de la carga
i) Dualidad de la carga: Todas las partículas cargadas pueden dividirse en
Es una magnitud fundamental de la física, responsable de la interacción positivas y negativas, de forma que las de un mismo signo se repelen
electromagnética. mientras que las de signo contrario se atraen.
En el S.I. La unidad de carga es el Culombio (C) que se define como la
cantidad de carga que fluye por un punto de un conductor en un segundo ii) Conservación de la carga: En cualquier proceso físico, la carga total de un
cuando la corriente en el mismo es de 1 A. sistema aislado se conserva. Es decir, la suma algebraica de cargas
positivas y negativas presente en cierto instante no varía.
1 nC = 10-9 C
iii) Cuantización de la carga: La carga eléctrica siempre se presenta como
Submúltiplos del 1 C = 10-6 C un múltiplo entero de una carga fundamental, que es la del electrón.
Culombio
1 mC =10-3 C
Expresión vectorial de la Ley de Coulomb
LEY DE COULOMB
Z
A lo largo de este tema estudiaremos procesos en los que la carga no varía con
el tiempo. En estas condiciones se dice que el sistema está en Equilibrio
  
Electrostático.
q1
r21  r2  r1 q2
 qq 
  F12  k 1 2 ur
r1 r2 2
r12
Enunciado de la Ley de Coulomb
Y
La fuerza ejercida por una carga puntual sobre otra está dirigida a lo largo de la X
línea que las une. Es repulsiva si las cargas tienen el mismo signo y atractiva si k: Constante de Coulomb, cuyo valor depende del sistema de unidades y
tienen signos opuestos. La fuerza varía inversamente proporcional al cuadrado del medio en el que trabajemos.
de la distancia que separa las cargas y es proporcional al valor de cada una de
ellas.
En el vacío S.I. k = 9·109 N m 2/C2

2. Constantes auxiliares
Permitividad del Vacío (o): Se define de forma que
1
k 
4  o
o= 8.85·10-12 C2/N m2
Si el medio en el que se encuentran las cargas es distinto al vacío, se comprueba
que la fuerza eléctrica es  veces menor, de esta forma se define la
Permitividad del Medio como  =  o.. Siendo  la Constante Dieléctrica del
Medio Así,
1
k'
4 

3. PRINCIPIO DE SUPERPOSICIÓN
A la hora de aplicar el principio de superposición debemos tener en cuenta dos
casos:
I) Campo eléctrico creado por una distribución discreta de carga en un
punto:
En este caso se calcula el campo eléctrico sumando vectorialmente los
campos eléctricos creados por cada una de las cargas puntuales en el punto
elegido.
Z
 P
q1 rp1 
 rpi  q 
q2 rp 2 qi E   k 2i ur
i rpi
Y
X

4. Dipolo eléctrico: Cálculo del campo eléctrico en un punto de la mediatriz de la
elé
línea que une ambas cargas.

E

 E
P

d E
r d

+q a a -q
Ejemplo
II) Campo eléctrico creado por una distribución continua de carga en un
punto:
P
En este caso dividimos la distribución
 en pequeños elementos diferenciales
Q
r de carga, dq, de forma que la
diferencial de campo eléctrico que crea
dq cada una de ellas es
 dq 
dE  k ur
r2
El campo eléctrico total para toda  dq 
la distribución será

E  k ur
r2

5. Dependiendo de la forma de la distribución, se definen las siguientes
distribuciones de carga
Lineal Superficial Volumétrica
dq dq dq
  
dl ds dv
Cálculo del campo eléctrico en cada caso:
 dl   ds   dv 

E  k  ur
L
r2
E k

r2
S
ur E k

r2
v
ur
Ejemplo 1: Campo eléctrico sobre el eje de una carga lineal finita.
x xo-x

6. Ejemplo 2: Campo eléctrico fuera del eje de una carga Ejemplo 3: Campo eléctrico creado por una distribución
lineal finita. uniforme de carga en forma de anillo de radio a, en un
punto de su eje.
d
Ejemplo 4: Campo eléctrico creado por una distribución
uniforme de carga en forma de disco de radio R, en un
punto de su eje.
dq
r
 P dEx X
x dEy

7. LÍNEAS DE CAMPO ELÉCTRICO
ELÉ

Las líneas de campo se dibujan de forma que el vector E sea tangente a ellas
en cada punto. Además su sentido debe coincidir con el de dicho vector.
Reglas para dibujar las líneas de campo
•Las líneas salen de las cargas positivas y entran en las negativas.
•El número de líneas que entran o salen es proporcional al valor
de la carga.
•Las líneas se dibujan simétricamente.
•Las líneas empiezan o terminan sólo en las cargas puntuales.
•La densidad de líneas es proporcional al valor del campo eléctrico.
•Nunca pueden cortarse dos líneas de campo.
EJEMPLOS DE LÍNEAS DE CAMPO ELÉCTRICO
LÍ ELÉ
Carga
puntual
Dipolo
eléctrico
Dos cargas
iguales
Q(-)=2Q(+)
Más ejemplos

8. Dipolo eléctrico encerrado en una superficie de forma
arbitraria
Ejemplo 2.- Supongamos un cilindro de radio R colocado en el seno de un campo
Superficie de forma arbitraria que incluye las cargas +2q y eléctrico uniforme con su eje paralelo al campo. Calcula el flujo de campo
–q. eléctrico a través de la superficie cerrada.
 El flujo total es la suma de tres términos,
ds dos que corresponden a las bases (b1 y
b2) mas el que corresponde a la superficie
cilíndrica. En ésta última el flujo es cero ya
 que los vectores superficie y campo son
E  perpendiculares. Así
ds    

E 
  E  ds  E  ds
b1

b2

ds

 E ds cos  
 E ds cos 0
El flujo sólo es proporcional a la carga
 0 que encierra una superficie, no a la
E forma de dicha superficie.

9. LEY DE GAUSS
E Considere la caja que se muestra en la fig. a, la que puede o no contener carga eléctrica.
La caja es de un material que no influye
en ninguno de los campos eléctricos. Nos
referimos a la caja como una superficie
cerrada, porque encierra un volumen.
¿Como se puede saber cuanta carga, en
su caso, hay dentro de la caja?
Anteriormente
aN
A Ahora nos : :
.
En las fig. a y b hay flujo eléctrico saliente y en c y d flujo eléctrico entrante.

10. Flujo eléctrico
El flujo eléctrico se representa por medio del número de líneas de campo
eléctrico que penetran alguna superficie.
Área A El número de líneas que penetra una
superficie es proporcional a EA.
Es decir el producto de la intensidad del
campo E por el área de la superficie
perpendicular A se llama flujo eléctrico .
 = EA
E
Si la superficie no es perpendicular al campo, el flujo es igual al producto
de la magnitud del campo por el área por el coseno del ángulo entre el
campo y la normal a la superficie.
Campo Eléctrico E uniforme
Normal

 = EAcos 

11. FLUJO ELÉCTRICO
ELÉ
Campo Eléctrico E No Uniforme
El flujo eléctrico da idea del número de líneas de campo que atraviesa cierta
superficie. Si la superficie considerada encierra una carga, el número de líneas
que atraviesa dicha superficie será proporcional a la carga neta.

ds  

E

  E  ds
s
Para una superficie cerrada el flujo será
negativo si la línea de campo entra y positivo si
sale. En general, el flujo neto para una
superficie cerrada será  

  E  ds
s
Ejemplo 1.- Flujo Eléctrico a través de una esfera.
Una carga puntual positiva q = 3 µC está rodeada por una esfera centrada en la
carga y cuyo radio es de 0,20 m. Hallar el flujo eléctrico a través de la esfera
La ley de Gauss
debido a esta carga.
En cualquier punto de la esfera la • La ley de Gauss constituye una de las
magnitud del campo eléctrico es leyes fundamentales de la Teoría
 q  Electromagnética.
E  k 2 ur
r
• Se trata de una relación entre la carga
encerrada en una superficie y el flujo de
su campo eléctrico, a través de la misma.
• Constituye un medio para obtener
expresiones de campos eléctricos, con
suficientes condiciones de simetría.

12. Una carga puntual q está situada en el centro de una superficie esférica de
Enunciado radio R. Calcula el flujo neto de campo eléctrico a través de dicha superficie.
El flujo de campo eléctrico a través de
cualesquier superficie cerrada (gaussiana), El campo eléctrico creado por una
carga puntual viene dado por
es igual a la carga neta encerrada, por la
 q 
misma, entre la constante  ds
 E  k 2 ur
r
 
  E
 E dA  qenc
 00 E dA  qenc
 R
En la superficie de la esfera se
cumple que r = R, luego
q
   qenc
 00EE  qenc  q 
E  k 2 ur
R
Para calcular el flujo a través de la superficie esférica, tenemos en
cuenta que el campo eléctrico es paralelo al vector superficie en cada
punto, por lo tanto
  q q

 E  ds 
 k
R 2
ds  k
R2  ds
El área de una superficie esférica viene dada por S =4R2, luego
kq
 4 R 2
R2
Flujo total:   4 k q El flujo es Independiente
del radio R de la esfera
Depende solo de la carga
q encerrada por la esfera.
El

13. Supongamos ahora una carga q próxima a una superficie cerrada
de forma arbitraria. En este caso el número neto de líneas de campo
que atraviesa la superficie es cero (entran el mismo número de
líneas que salen), por lo tanto
0
q
El flujo a través de una superficie
que no encierra carga es nulo.
Ecuación valida para una superficie de cualquier
forma o tamaño, con la sola condición que sea
una superficie cerrada que encierre la carga q.
Aplicación de la ley de Gauss para
Si
el cálculo de E
Encontrar el flujo
eléctrico neto a través
de la superficie si:
q1=q4=+3.1nC,
q2=q5=-5.9nC,
and q3=-3.1nC?
qenc q1  q2  q3
   670 N  m 2 / C
0 0

14. Superficies esfericas Gaussianas Campo Eléctrico de una carga
puntual
Considere una carga puntual q. El flujo en una
esfera de radio r será:
q
   E  dA  E  dA  E 4 r 2 
0
E  q / 4r 2 0
dA E
r
a) carga puntual positiva a) carga puntual negativa q
Flujo Positivo Flujo Negativo

16. TEOREMA DE GAUSS I Consideremos varias superficies centradas
en una esférica que contiene una carga q.
Este teorema da una relación general entre el flujo de campo eléctrico a través
de una superficie cerrada y la carga encerrada por ella.
s3
s1 s2
q El flujo a través de la superficie
Ya hemos visto que el flujo neto a través de una superficie esférica viene dado esférica es
por
q
  4 k q   4 k q 
o
Vamos a comprobar que este flujo es independiente de la Como el número de líneas que atraviesan las tres superficies es el
forma de la distribución. Sólo depende de la carga que haya en mismo, se cumple que
el interior. 1   2  3
Por lo tanto el flujo es independiente de la forma de
la superficie.
Generalización de los resultados Enunciado del Teorema de Gauss
Para distribuciones de carga, ya sean discretas o continuas, podemos El flujo eléctrico neto a través de cualquier superficie gaussiana cerrada es igual
aplicar el principio de superposición. a la carga neta que se encuentre dentro de ella, dividida por la permitividad del
vacío.
Ejemplo:
S’ q1 Esta ley sólo puede aplicarse a problemas con
q2  ( S)  gran simetría.
S
q3
o
(q2  q3 ) Procedimiento para aplicar el teorema de Gauss
q1
 ( S' ) 
S’’ o  
Dada una distribución
 ( S' ' )  0 E paralelo a ds
de carga, buscar una en todos los puntos de la
superficie gaussiana  superficie
que cumpla estas E constante
  q condiciones

 E  ds  int
o

17. El flujo eléctrico a través de una superficie cerrada viene dado por
  q

 E  ds  int
o
Si la superficie cerrada gaussiana cumple las dos condiciones anteriores
 
 E  ds 
 
E ds  E ds  E s
S es el área de la superficie
Por lo tanto q gaussiana
E S  int
o qint es la carga encerrada en
dicha superficie
Ejemplo 1: Campo eléctrico próximo a un plano infinito de Ejemplo 2: Campo eléctrico a una distancia r de una carga
carga. lineal infinitamente larga de densidad de carga uniforme .

18. Ejemplo 3: Campo eléctrico debido a una corteza esférica Ejemplo 4: Campo eléctrico debido a una esfera
uniformemente cargada. uniformemente cargada.