Este capítulo cubre los siguientes temas:
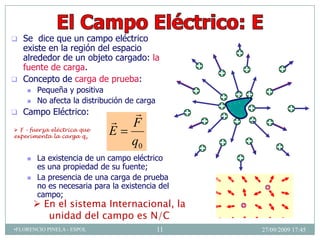
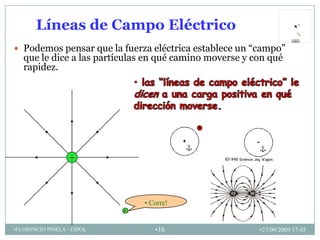
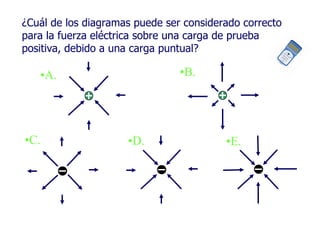
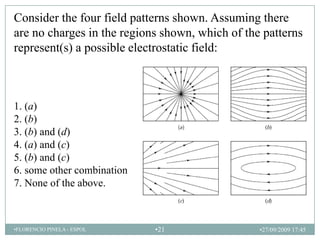
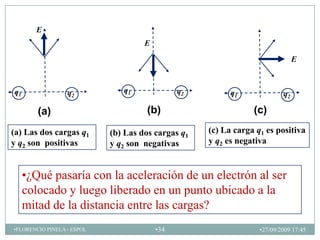
1) La definición y propiedades del campo eléctrico, incluyendo líneas de campo eléctrico.
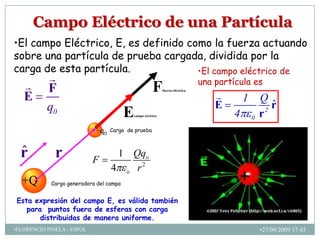
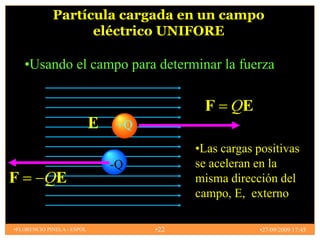
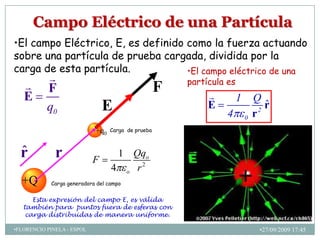
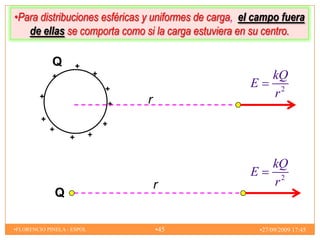
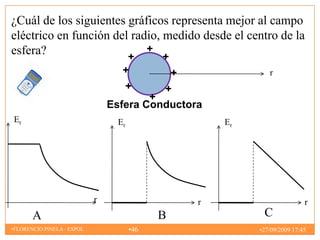
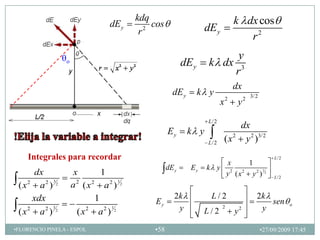
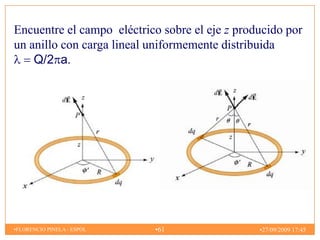
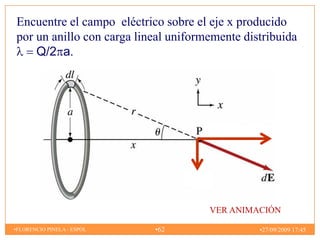
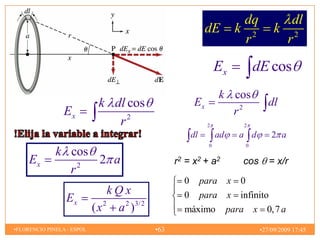
2) El campo eléctrico creado por partículas puntuales y distribuciones continuas de carga.
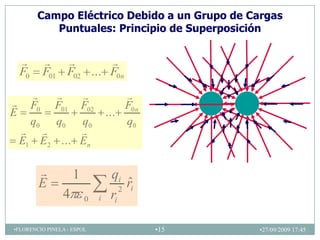
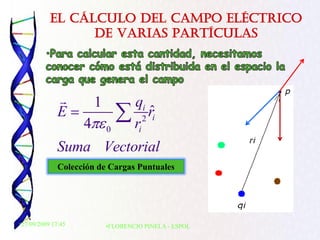
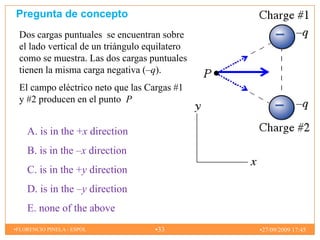
3) El principio de superposición para calcular el campo eléctrico creado por múltiples cargas.