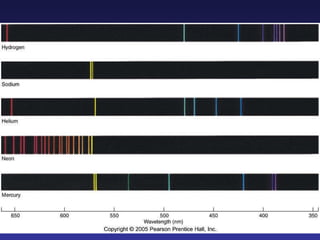
El documento presenta un resumen de la teoría cuántica y la estructura electrónica de los átomos. Explica cómo la teoría cuántica predijo la naturaleza cuántica de los electrones y su comportamiento ondulatorio, lo que llevó al desarrollo de modelos atómicos como los de Planck, Bohr, De Broglie y Schrödinger. También describe los cuatro números cuánticos que definen los estados electrónicos y cómo se organizan los electrones en las capas electrónicas de los á

1. Treinta radios se unen en el centro; Gracias al agujero podemos usar la rueda. El barro se modela en forma de vasija; Gracias al hueco puede usarse la copa. Se levantan muros en toda la tierra; Gracias a la puertas se puede usar la casa. Así pues, la riqueza proviene de lo que existe, Pero lo valioso proviene de lo que no existe. Lao Tse - Tao Te Ching

2. Teoría cuántica y la estructura electrónica de los átomos

3. Introducción Estudiaremos el desarrollo de la teoría cuántica Ayuda a predecir y entender la función que desempeñan los electrones en la química

4. Preguntas El estudio de los átomos nos lleva a las siguientes preguntas: ¿Cuántos electrones están presentes en un determinado átomo? ¿Qué energía tiene un electrón? ¿En que parte del átomo se encuentran los electrones?

5. Representación del átomo

6. El nacimiento de una nueva física Hasta comienzos del siglo XX, se intentó asimilar el comportamiento de los átomos con la mecánica clásica (Newtoniana) En 1900 comenzó una nueva era, de manos de un físico alemán, Max Planck.

7. Ondas Para comprender la teoría cuántica, debemos tener conocimiento de la naturaleza de las ondas. Una onda es una alteración vibrátil mediante la cual se puede transmitir energía

9. Propiedades de las ondas Sus propiedades características son su longitud y altura, así como el número de ondas que pasa por determinado punto en un segundo

10. Problemas 1) Las microondas se utilizan para transmitir información. ¿Cuál es la longitud de onda de una microonda que tiene una frecuencia de 3,44 * 10 9 Hz? 2) Una radio popular tiene una frecuencia de 96,3 MHz. ¿Cuál es la longitud de onda de la emisión?

12. Teoría cuántica de Planck Los sólidos calentados emiten radiación electromagnética

13. Teoría cuántica de Planck La cantidad de energía emitida depende de la longitud de onda ( λ )

14. Teoría cuántica de Planck (1900) Planck supuso que las moléculas emitían energía sólo en cantidades discretas, como pequeños paquetes Los llamó quanta o cuantos La energía de un cuanto es E = h . v Donde h es la constante de Planck, cuyo valor es 6,63 * 10 -34 J.s

15. Problemas 1) Calcule la energía de cada uno de los siguientes tipos de radiación: a. 6,32*10 20 Hz, b.9,50*10 13 Hz, c.1,05 *10 16 Hz 2) Indique en qué parte del espectro se encuentran cada una de las radiaciones del ejemplo anterior

16. El efecto fotoeléctrico (1905)

20. El efecto fotoeléctrico (1905) Einstein supuso que un rayo de luz es en realidad un torrente de partículas (fotones) La energía de un fotón puede calcularse con la ecuación de Planck Este trabajo le valió el premio Nobel en 1921

21. Teoría de Bohr El “misterio” de los espectros de emisión

23. Espectros de emisión y absorción

25. Espectro del átomo de hidrógeno Bohr supuso que las órbitas permitidas a un electrón también estaban “cuantizadas” La emisión de radiación se debía a la “caída” de un electrón desde una órbita de mayor energía a una de menor energía Demostró que la energía de un electrón es: E n = -R h (1/n 2 ) R h = 2,18 * 10 -18 J

26. Orbitas atómicas (teoría de Bohr)

28. Niveles de energía y espectros de emisión

29. Espectro del átomo de hidrógeno Bohr nos dejó un modelo de átomo similar al sistema solar Si los electrones se comportaran de esta forma, emitirían luz, perderían energía y caerían sobre el núcleo Un átomo de hidrógeno duraría menos de un segundo

30. La naturaleza dual del electrón Louis De Broglie aclaró el motivo porque las órbitas están cuantizadas Consideró que los electrones se comportan como ondas Relacionó las propiedades como λ = h / (m.v)

33. Mecánica Cuántica La teoría de Bohr no podía explicar los espectros de átomos polielectrónicos. Se detectaban electrones del mismo nivel que tenían energías distintas Otro problema era la ubicación de la “onda” del electrón

34. Principio de Incertidumbre Werner Heisemberg formuló una teoría conocida ahora como “principio de incertidumbre” Es imposible conocer la velocidad y la posición de una partícula simultáneamente Se expresa como Δ x. Δ p ≥ h/(4. π )

35. La mecánica cuántica Una consecuencia del principio de Incertidumbre, es que las órbitas no pueden ser regulares Erwin Schr ödinger formuló una ecuación, introduciendo el concepto de orbital y densidad electrónica; además de incluir las propiedades ondulatorias y de partículas.

36. El orbital atómico y los números cuánticos

37. Estructura de la capa de electrones Resumiendo la teoría cuántica: Los átomos pueden absorber o emitir porciones discretas de energía Un cambio en el estado de energía está relacionado con un cambio en la capa de electrones Los electrones de un átomo “ocupan “ estados de energía discretos. Estos estados están determinados por 4 números cuánticos

38. Números Cuánticos Derivan de la solución de la ecuación de Schr ödinger. Número Cuántico Principal (n): puede tomar valores enteros 1,2,3,etcétera Está relacionado con la distancia promedio del electrón al núcleo A mayor n, mayor distancia. Está relacionado con el nivel de energía

39. Número Cuántico Principal 1s, 2s, 3s 3s 2s 1s

40. Número cuántico angular (l) Toma valores desde 0 hasta n-1 Determina la “forma” de los orbitales, son los “subniveles” de energía Tiene nombres especiales: 0 --------------------- s, por “sharp”, o brillante 1 --------------------- p, por “principal” 2 --------------------- d, por “diffuse” o difuso 3 --------------------- f, por “fundamental” A partir de aquí, el orden es alfabético, el 4 es g, el 5 es h, etc

41. Número cuántico angular (l)

42. Número cuántico magnético m l Describe la orientación del orbital en el espacio. Toma valores desde – l hasta l Por ejemplo, para l = 2 (orbital d) existen cinco valores posibles: -2, -1, 0, 1, 2 Esto evidencia que hay 5 orbitales de subnivel de energía 2

43. Número Cuántico espín (m s ) Ante la aplicación de un campo magnético, las líneas de emisión podían separarse En consecuencia, se supuso que los electrones se comportaban como pequeños imanes Al existir dos posibilidades de giro, se le asignaron valores + ½ y -½

45. ¿Cómo se construyen las capas? 1 . Los niveles de energía más bajos son ocupados primero 1s < 2s < 2p < 3s < 3p < 4s < 3d < 4p < 5s < 4d < 5p < 6s < 4f < 5d < 6p < 7s < 5f < 6d < 7p

46. 2 . Principio de Pauli : un átomo no puede tener dos electrones con los cuatro números cuánticos idénticos Conclusión: en un orbital atómico los electrones deben tener números cuánticos de spin opuestos. Si los electrones de un orbital tuvieran el mismo espín, los campos magnéticos se reforzarían El helio sería Paramagnético (atraído por un imán). Sin embargo es diamagnético (no tiene magnetismo) – por lo tanto los espines deben cancelarse

47. ¿Cómo se construyen las capas? 3 . Regla de Hund : los orbitales se ocupan de tal forma que el número de electrones con la misma orientación de spin se maximizan.

48. Problemas 1) a) ¿Cómo se designan todos los subniveles correspondientes al nivel n=4? b) ¿Cuántos orbitales hay en estos subniveles? 2) Obtenga el número total de orbitales para n = 2 3) Escriba los números cuánticos de cada uno de los electrones del Be