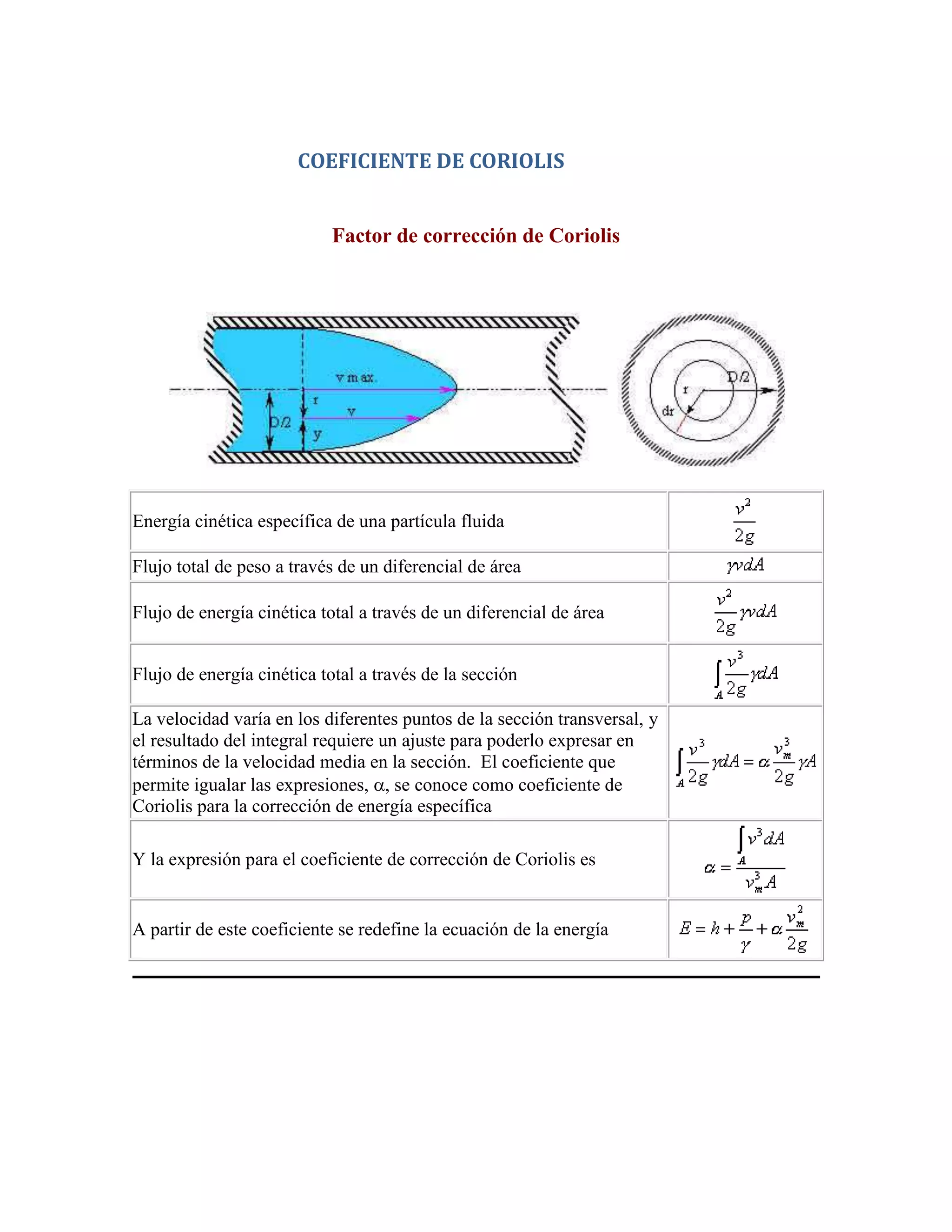
Este documento describe los coeficientes de Coriolis y Boussinesq, que son factores de corrección utilizados para expresar el flujo total de energía cinética o cantidad de movimiento a través de una sección en términos de la velocidad media, debido a que la velocidad varía en diferentes puntos de la sección transversal. Define las expresiones matemáticas para estos coeficientes y explica cómo se redefinen las ecuaciones de energía y fuerza dinámica a partir de ellos. También incluye ejemplos de cálculos de estos

1. COEFICIENTE DE CORIOLIS
Factor de corrección de Coriolis
Energía cinética específica de una partícula fluida
Flujo total de peso a través de un diferencial de área
Flujo de energía cinética total a través de un diferencial de área
Flujo de energía cinética total a través de la sección
La velocidad varía en los diferentes puntos de la sección transversal, y
el resultado del integral requiere un ajuste para poderlo expresar en
términos de la velocidad media en la sección. El coeficiente que
permite igualar las expresiones, , se conoce como coeficiente de
Coriolis para la corrección de energía específica
Y la expresión para el coeficiente de corrección de Coriolis es
A partir de este coeficiente se redefine la ecuación de la energía

2. Calcular el coeficiente de corrección de velocidad para las distribuciones de velocidad:
v =
sen
(h2 - z2)i
2
v = vo.(z/e)
v=vo(1-(r/R)2
))i
Coeficiente de Boussinesq
Factor de corrección de Boussinesq
Flujo de cantidad de movimiento a través de un diferencial de área
Flujo total de cantidad de movimiento a través de la sección
La velocidad varía en los diferentes puntos de la sección transversal, y
el resultado del integral requiere un ajuste para poderlo expresar en
términos de la velocidad media en la sección. El coeficiente que
permite igualar las expresiones, , se conoce como coeficiente de
Boussinesq para la corrección de la cantidad de movimiento
Y la expresión para el coeficiente de corrección de Boussinesq es
A partir de este coeficiente se redefine la ecuación de fuerza dinámica

3. Calcular el coeficiente de corrección de cantidad de movimiento para las
distribuciones de velocidad:
v =
sen
(h2 - z2)i
2
v = vo.(z/e)
v=vo(1-(r/R)2
))i
Explique por qué la ecuación de la energía, con flujo no permanente, debe expresarse
así: