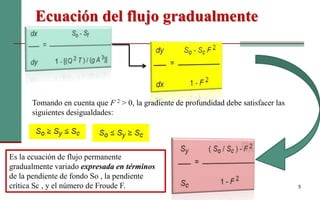
Este documento describe las curvas de remanso en el flujo gradualmente variado. Explica que las curvas de remanso se expresan en términos de la pendiente crítica y clasifican el flujo como subcrítico o supercrítico dependiendo de si la pendiente es menor o mayor que la pendiente crítica. También describe los diferentes tipos de curvas de remanso que pueden ocurrir debido a cambios en la pendiente, como de pendiente suave a pendiente fuerte.

1. Curvas de Remanso

2. CURVAS DE REMANSO
 El cálculo del flujo gradualmente variado es parte de la
práctica de la ingeniería hidráulica.
 La ecuación convencional del flujo gradualmente variado se
expresa en función de la pendiente de fondo So, la
pendiente de fricción Sf, y el número de Froude F
 Las curvas de remanso se expresan en términos de la
pendiente crítica Sc .
 De esta manera, se demuestra que la gradiente de
profundidad dy/dx está físicamente limitada a valores fuera
del rango comprendido entre Sc y la pendiente de fondo So.
.

3. Ecuación del flujo gradualmente
variado
 en la cual y = profundidad,
 x = distancia a lo largo del canal,
 dy/dx = gradiente de
profundidad,
 Q = caudal o descarga,
 T = ancho de la superficie libre,
 A = área de flujo, y g = aceleración
de la gravedad.
 Esta ecuación es válida para pendientes pequeñas (So < 0.1), lo
cual es el caso típico.

4. en la cual R = A/P = radio hidráulico,
P = perímetro mojado,
 El número de Froude en términos de descarga Q es (Chow
1959):
Combinando las ecuaciones las 2 ecuaciones se
obtiene:
En el flujo normal crítico F = 1, y la pendiente de
fricción para el flujo crítico, es decir, la pendiente
crítica, es::
la gradiente de profundidad se redefine como Sy = dy/dx.
Resolviendo la ecuación 6 para el número de Froude:

5. Ecuación del flujo gradualmente
variado
5
Tomando en cuenta que F 2 > 0, la gradiente de profundidad debe satisfacer las
siguientes desigualdades:
Es la ecuación de flujo permanente
gradualmente variado expresada en términos
de la pendiente de fondo So , la pendiente
crítica Sc , y el número de Froude F.

6. Clasificación de las curvas de remanso
 El flujo sub normal se define como aquel
para el cual la profundidad es menor que la
profundidad normal (𝐹2 > 𝑆𝑜/𝑆𝑐)
.
Clasificación de curvas de remanso basada solamente en los
tres parámetros adimensionales: Sy /Sc , So /Sc , y F

7. Clasificación y nomenclatura
• Pendiente Suave(Mild) Yn>Yc
• Pendiente Critica(Critical) Yn=Yc
• Pendiente Fuerte (Steep) Yn<Yc
• Pendiente Horizontal Yn= Infinito
 Ecuacion de manning
• Pendiente Adversa (contra la gravedad)
7

8. Los tipos de pendientes que se presentan en el flujo
gradualmente variado son:
a) Positivos:
Critico (C)
Suave (M)
Pronunciado (S)
b) Horizontales (H)
c) Adversa (A).
8
Tipos de pendiente

9. Zonas de generación de las curvas de
remanso
9
• Zona 1
• Zona 2
• Zona 3

10. 10
 Zona 1. El espacio por encima de la línea superior; se presenta el flujo
subcrítico tirante normal (dn) y el perfil del flujo. Flujo supercrítico: el
tirante critico (dc) y perfil de flujo
 Zona 2. El espacio entre las dos líneas, se presenta el flujo subcrítico,
tirante crítico (dc) y tirante normal (dn), se presenta también el flujo
supercrítico; tirante normal (dn) y tirante crítico (dc)
 Zona 3. El espacio por debajo de la línea inferior, se presenta el flujo
subcrítico: plantilla el canal y tirante crítico, supercrítico; plantilla del
canal y tirante normal.

11. Curvas de remanso por cambios de
pendiente
 En el diseño de canales se pueden presentar curvas de
remanso en pendientes suaves y fuertes.
Aunque pueden existir las pendientes horizontal, adversa y
critica, es poco probable que como diseñador, lo podamos
incluir en algún trabajo. se presentan seis casos generales.
 De pendiente suave a pendiente más suave.
 De pendiente suave a pendiente menos suave.
 De pendiente suave a pendiente fuerte.
 De pendiente fuerte a pendiente menos fuerte.
 De pendiente fuerte a pendiente suave.
11

12. 1.De pendiente suave a pendiente más suave.
Sean 𝑌𝑛1, 𝑌𝑛2 los tirantes normales en cada uno de los tramos.
• En el primer tramo, por ser pendiente suave (flujo
subcrítico), se cumple que, 𝑌𝑛1 > 𝑌𝑐.
• En el segundo tramo, por ser pendiente más suave (flujo
subcrítico), también se cumple que 𝑌𝑛2 > 𝑌𝑐.
• La profundidas normal del segundo tramo, es mayor que la
del primero, porque su pendiente es menor que la del
primero. Por lo tanto, 𝑌𝑛2 > 𝑌𝑛1.
Como toda singularidad (en este caso, el cambio de
pendiente) en un flujo subcrítico, crea efectos hacia aguas
arriba, por lo que en el segundo tramo se produce un flujo
uniforme, mientras que en el primer tramo se presenta una
curva M1. La curva M1 se calcula de la sección de control
que es el cambio de pendiente, con un tirante real 𝑌𝑛2, hacia
aguas arriba hasta un 𝑌𝑓 = 1.02𝑦 𝑛1.

13. 2. De pendiente suave a pendiente menos suave.
Por consideraciones similares es al caso 1 se tiene que: 𝑌𝑛2 < 𝑌𝑛1
• En ambos tramos se cumple que:
𝑌𝑛1 > 𝑌𝑐 (Pendiente suave)
𝑌𝑛2 > 𝑌𝑐 (Pendiente menos suaves)
• Como toda singularidad (en este caso, el cambio de
pendiente) en un flujo subcritico, crea efectos hacia
aguas arriba, por lo que en el segundo tramo se
produce un flujo uniforme, mientras que en el primer
tramo se produce un flujo uniforme, mientras que en el
primer tramo se presenta una curva M2. La curva M2
se calcula de la sección de control que es el cambio de
pendiente, con un tirante real 𝑌𝑛2, hacia aguas arriba
un 𝑌𝑓 = 0.98𝑌𝑛1.

14. 3. De pendiente suave a pendiente fuerte.
Sean 𝑌𝑛1, 𝑌𝑛2 los tirantes normales en cada uno de los dos tramos.
• En el primer tramo, por ser pendiente suave (flujo subcritico), se cumple
que, 𝑌𝑛1 > 𝑌𝑐.
• En el segundo tramo, por ser pendiente fuerte (flujo supercritico), se
cumple que 𝑌𝑛2 < 𝑌𝑐.
• Para pasar de un flujo subcritico (primer tramo) a un flujo supercrítico
(segundo tramo), en el cambio de pendiente, que es la sección de control,
se produce el 𝑌𝑐.
Como toda singularidad (en este caso, el cambio de pendiente) en un flujo
subcritico, crea efectos hacia aguas arriba, en el primer tramo se presenta
una curva M2. La curva M2 se calcula de la sección de control con un
tirante real 𝑌𝑐, hacia aguas arriba, hasta un 𝑌𝑓 = 0.98𝑌𝑛1.
Como toda singularidad (en este caso, el cambio de pendiente) en un flujo
supercrítico, crea efectos hacia aguas abajo, en el segundo tramo se presenta
una curva S2. La curva S2 se calcula de la sección de control con un tirante
real 𝑌𝑐, hacia aguas abajo, hasta un 𝑌𝑓 = 1.02𝑌𝑛2.

15. efg 15
DE PENDIENTE FUERTE A
PENDIENTE MENOS FUERTE
DE PENDIENTE FUERTE A
PENDIENTE MAS FUERTE
DE PENDIENTE FUERTE
A PENDIENTE SUAVE.

16. CURVAS DE REMANSO

18. efg 18

19. efg 19

20. La pendiente de fricción se debe determinar a partir de alguna ecuación de resistencia al flujo, por
ejemplo la de Manning.
El proceso de cálculo es usualmente el siguiente:
1. Determinar parámetros básicos de diseño: topografía, suelos, caudal, etc.
2. Diseñar completamente el canal por tramos y conocer todos los elementos.
3. Determinar el tipo de pendiente del canal: subcrítica, supercrítica, crítico, horizontal o adversa.
4. Identificar los controles del flujo: compuertas, presas, vertederos, cambios de pendiente y caídas.
5. Determinar los elementos hidráulicos en la sección de control.
6. Analizar los perfiles de flujo que se presentan aguas arriba y aguas abajo del control:
M, S, C, H,A.
7. Calcular los perfiles de flujo a partir de la sección de control.
En general, existen dos casos de cálculo:
a) Solución directa. Se conoce la variación de profundidades del agua dy y el problema es
encontrar la distancia entre ellas (dx).
b) Solución por iteraciones. Se desconoce la variación de profundidades del agua (dy) y se
conoce la distancia entre ellas (dx). Como tanto Sf como FR son funciones de y; y ésta solo se
conoce en la sección de control, la profundidad del agua en la siguiente sección debe encontrarse por
aproximaciones sucesivas.
20

21.  A través de un canal que termina en caída brusca, circulan 4.5 m3/s
de agua. Sabiendo que b = 1.85 m; S0 = 0.002 m/m y n = 0.012
(Manning).
 Se pide determinar mediante el método de integración gráfica,
el perfil de la línea de superficie libre a partir de la arista de la
caída brusca.
 Datos: Q=4.5 m3/s, b=1.85 m , S0=0.002 , n=0.012
Solución:
Determinación del tirante normal, aplicando la ecuación general
𝑸∗𝒏
𝑺
=AR2/3
21

22.  Si sabemos que: A=bdn=1.85dn
 P=b+2dn =1.85+2dn
 R=A/P = (1.85dn /1.85+2dn)
 Para la determinación del valor de dn se hará mediante
iteraciones.
 Se propone un dn=1.05:
22

23.  Se acepta el valor del tirante dn=1.05 m
 Determinación del valor del gasto unitario: q=Q/B
q=4.5 /1.85 = 2.43 m3/s
 Determinación del valor de dc:
 Como hay caída brusca, la profundidad del escurrimiento debe
estar entre dn y dc.
 Por lo consiguiente dn>d>dc.
 Determinación de la velocidad crítica y área crítica.
23

24.  Determinación del perímetro mojado y radio hidráulico en la
sección crítica:
 Determinación de la pendiente crítica:

 Como Sc>S. la pendiente es suave y la línea de la superficie
libre es de la clase M tipo 2 (M2).
 Para el cálculo mediante el método de integración grafica
calculamos Kn y Zn.
 Cálculo del factor de transporte o de conductividad Kn. 24

25.  Para el cálculo mediante el método de integración grafica
calculamos Kn y Zn.
 Cálculo del factor de transporte o de conductividad Kn.
 Cálculo del factor de sección Zn:
25

26. 26

27. Datos para el perfil mediante el método de integración
gráfica.
27
Como dn>d>dc
el tipo de perfil es
M2,

28. Método del paso estándar
 Este método es muy apropiado aplicarlo para canales no prismáticos
(canales naturales).
 En canales no prismáticos los elementos hidráulicos no son
independientes de la distancia a lo largo del canal. Este cálculo se lleva
a cabo mediante pasos de estación a estación en las cuales se han
determinados las características hidráulicas.
 En tales casos la distancia entre las estaciones es conocida y el
procedimiento es determinar la profundidad del flujo en las estaciones.
 Tal procedimiento a menudo se lleva a cabo mediante un proceso de
ensayo y error.
 Para explicar este método es conveniente referir la posición de la
superficie libre del agua con respecto a un nivel de referencia
horizontal.
28

29. Tramo de canal para la deducción del paso estándar.
29

30.  Estableciendo Bernoulli entre la sección 1 y 2 se tiene:
 La pérdida de carga por fricción es :
 Donde la pendiente por fricción SE se toma como el promedio
de las pendientes en las dos secciones extremas.
 Las alturas totales en las dos secciones extremas son:
 y
 por consiguiente la ecuación se convierte en:
 Esta es la ecuación básica que define el procedimiento del
método del paso estándar 30

31. Esta es la ecuación básica que define el procedimiento del
método del paso estándar
donde:
H = energia total, en m
d1 = energía potencial o de presión , en m
Z = energía de posición en la sección 1.
hf1-2= pérdida de carga por fricción , en m
 Tabla para el cálculo del perfil de la superficie libre del agua
mediante el método del paso estándar.
31

32.  Columna 1: Sección identificada por un número de estación, tal como
"Estación 1 + 55". La localización de las estaciones está fija en las
distancias determinadas, en la columna 12 se dan como datos las
distancias, las segunda estación se obtiene con la sumatoria de la
primera distancia más el valor de la segunda distancia, y así
sucesivamente se van calculando los valores de las demás estaciones.
 Columna 2: Elevación de la superficie libre del agua en la estación.
Inicialmente se introduce un valor de prueba en esta columna; ´este será
aceptado o rechazado con base en los cálculos hechos en las siguientes
columnas de la tabla. Para el primer paso esta elevación debe darse o
suponerse. Cuando el valor de prueba del segundo paso ha sido
verificado, se convierte en la base para la verificación del valor de
prueba en el siguiente paso y así sucesivamente. Compleméntese, la
obtención del valor de esta columna, con lo indicado para obtener el
valor de la columna 15. 32

33.  Columna 3: Profundidad de flujo en pies, correspondiente a la elevación de
la superficie del agua de la columna 2. Por ejemplo, la profundidad de flujo
en la estación 1+55 es igual a la elevación de la superficie del agua menos
la elevación en el sitio de presa menos (distancia desde el sitio de presa
multiplicada por la pendiente del lecho), ó 605.048 -600.000 - 155 X 0.0016
= 4.80 pies
 Columna 4: cálculo del área mojada correspondiente a “d” de la columna 3.
 Columna 5: Velocidad media; Vm=Q/A (área columna 4).
 Columna 6: carga velocidad o altura de velocidad correspondiente a la
velocidad, columna 5.
 Columna 7: Altura total calculada mediante la expresión H1=z1 + d1
+V2/2g, igual a la suma de “Z” (columna 2) más la altura de la velocidad
(columna 6).
 Columna 8: Radio hidráulico, correspondiente a “d” de la columna 3
deberá determinarse el perímetro mojado de la sección de análisis.
33

34.  Columna 8: Radio hidráulico, correspondiente a “d” de la columna 3 deberá
determinarse el perímetro mojado de la sección de análisis.
 Columna 9: Radio hidráulico elevado a la potencia 4/3.
 Columna 10: Cálculo de la pendiente hidráulica: Sf =>
 Columna 11: Pendiente hidráulica o de fricción promedio a traves del tramo entre
las secciones de cada paso.
 Columna 12: Longitud del tramo entre las secciones, igual a la diferencia de los
números de estación entre las estaciones.
 Columna 13: cálculo de las pendientes por fricción entre las secciones 1 y 2, igual
al producto de los valores de las columnas 11 y 12, es decir:

34

35.  Columna 14:Pérdidas por remolino del tramo, iguales a cero.
 Columna 15: Elevación de la altura total en m o pies. Esta se calcula
mediante la suma de los valores de hf y he de las columnas 13 y 14 más la
elevación del extremo más bajo del tramo, el cual se encuentra en la columna
15 del tramo anterior (fila de arriba columna 15). Si el valor que se obtiene es
sensiblemente igual al de la columna 7, es decir al primer H, se supone un
nuevo valor para la elevación Z de la superficie del agua (columna 2), y así
sucesivamente, hasta que estos dos valores sean sensiblemente iguales. El valor
que produce este resultado es la elevación correcta de la superficie del agua.
35

36.  Ejemplo. Un canal trapecial conduce un gasto de 11.327m3/seg, con un
ancho de plantilla de b= 6.096 m, talud 2:1, pendiente longitudinal del
canal So = 0.0016 y n =0.025.
 Calcule el perfil del flujo, Mediante el método del paso estándar
determine el tipo de perfil.
 Creado por una presa que embalsa el agua hasta una profundidad de 1.524
m inmediatamente detrás de la presa.
 Se supone que el extremo de aguas arriba del perfil es igual a una
profundidad 1% mayor que la profundidad normal.
 Suponga que las estaciones a lo largo del canal están fijadas en las
distancias que se dan como dato en la columna 12.
 La elevación en el sitio de la presa es de 182.88 m.
 Datos: Q=11.327m3/seg; b= 6.096 m ; m =2:1; n=0.025 ; So =0.0016;
P=1.524 m elevación Presa =182.88 m.
efg 36

37. Perfil de la Superficie Libre del Agua mediante el método del paso
estándar (sistema
métrico)
efg 37

38. Introducción
 Para conocer el régimen hidráulico a lo largo de un
canal se define el numero de froude, el cual
permite clasificar diferentes condiciones de la
corriente de agua

39. Número de Froude
 El número de Froude cuya abreviatura es Fr,
es un número adimensional, el cual relaciona
el efecto de las fuerzas de inercia con las
fuerzas de gravedad las cuales actúan sobre
un fluido.
 𝐹𝑟 =
𝐹𝑢𝑒𝑟𝑧𝑎𝑠 𝑑𝑒 𝐼𝑛𝑒𝑟𝑐𝑖𝑎
𝐹𝑢𝑒𝑟𝑧𝑎𝑠 𝑑𝑒 𝑔𝑟𝑎𝑣𝑒𝑑𝑎𝑑

40.  Cuando el número de Froude se encuentra en
canales abiertos informa sobre el estado del flujo
hidráulico, mientras que cuando el número de
Froude se encuentra en un canal se conoce como:
 𝐹𝑟 =
𝑣
𝑔∗ 𝑦

41. El flujo se clasifica como:

42. Ejemplo
 Un canal rectangular de 1830 m de longitud, 18.3 m de ancho y 3.05 de
profundidad transporta 50.94 m3/seg. de agua (C=40). La limpieza del
canal hace que aumente C a 55 si la profundidad en el extremo superior
permanece a 3.05 m, hallar la profundidad en el extremo inferior para el
mismo caudal (aplicando un solo tramo).
Datos
L=1830 m B=18.30 m Q=50.94 m3/seg C=40
La limpieza del canal hace que el coeficiente:
C=55 d1=3.05 d2=?
42

43. A1 =bd = 18.3(3.05) =55.82 m2
P=b + 2d =18.3 +2(3.05) =24.4 m
R=A/P = 55.82/24.4 = 2.287 m
V1 =Q/P = 50.94 n/55.82 =0.912 m/s
Cálculo de la pendiente del canal (S0) a partir de la ecuación de
Chezy: V=C 𝑅𝑆
 Cálculo de la energía especifica en la sección 1 del canal:
43

44.  Cálculo del tirante d2 a partir de la fórmula
 Si consideramos que SE=0 por lo tanto
44

45.  >>>>
 Se propone un d2=3.274 m
 Por lo tanto el
tirante supuesto
es el correcto
45

46. efg 46