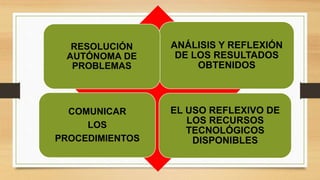
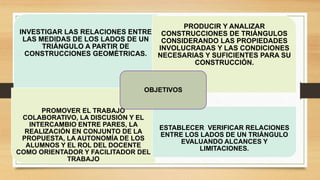
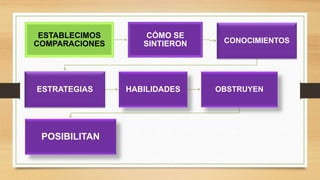
El documento presenta una propuesta didáctica para enseñar geometría en el aula a través del uso del programa GeoGebra. La propuesta involucra la construcción y análisis de triángulos considerando sus propiedades, así como la discusión y resolución colaborativa de problemas geométricos utilizando la herramienta tecnológica.

1. COLOQUIODE MATEMÁTICA
CANCIO, SANDRA GABRIELA

2. En el apartado Reconsiderar del Cuadernos para el
Aula, sostiene que CADA PERSONA SE VA
FORMANDO EN LA MATEMÁTICA, DEPENDIENDO
DEL MODO EN QUE VA CONOCIENDO Y USANDO
LOS CONOCIMIENTOS MATEMÁTICOS.

3. Skovmose y Valero (2012) señalan que NO
BASTA UN ACCESO UNIVERSAL A LA
ESCUELA PARA QUE ÉSTE SEA
DEMOCRÁTICO, ES NECESARIA LA
INCLUSIÓN, PARA QUE TODOS PUEDAN
DOMINAR IDEAS MATEMÁTICAS
PODEROSAS, SIN SER SOLO
ESPECTADORES.

4. LA FORMACIÓN MATEMÁTICA
DEBIERA CENTRARSE:

5. ANÁLISIS Y REFLEXIÓN
DE LOS RESULTADOS
OBTENIDOS
EL USO REFLEXIVO DE
LOS RECURSOS
TECNOLÓGICOS
DISPONIBLES
COMUNICAR
LOS
PROCEDIMIENTOS
RESOLUCIÓN
AUTÓNOMA DE
PROBLEMAS

6. Como se hace matemática en el aula define:
QUÉ MATEMÁTICA SE HACE,
PARA QUÉ
Y PARA QUIÉNES se la enseña.

7. GEOGEBRA, POR SU CARÁCTER DINÁMICO,
PERMITE REALIZAR CONSTRUCCIONES SIN
MEDIDAS, FAVORECIENDO QUE SE CONVIERTAN EN
OBJETO DE ANÁLISIS Y EXPLORACIÓN LAS
RELACIONES INHERENTES A CADA FIGURA.

8. RAZONAR EN GEOMETRÍA CONSISTE EN
APOYARSE EN PROPIEDADES CONOCIDAS PARA
PODER ANTICIPAR RELACIONES NO CONOCIDAS,
INFERIR PARA LUEGO DEDUCIR NUEVAS
PROPIEDADES (ITZCOVICH, 2005).

9. MI PROPUESTA DE ENSEÑANZA FUE PRODUCIR Y
ANALIZAR DIFERENTES CONSTRUCCIONES DE
TRIÁNGULOS CONSIDERANDO LAS PROPIEDADES
INVOLUCRADAS Y LAS CONDICIONES NECESARIAS
Y SUFICIENTES PARA SU CONSTRUCCIÓN.

10. INVESTIGAR LAS RELACIONES ENTRE
LAS MEDIDAS DE LOS LADOS DE UN
TRIÁNGULO A PARTIR DE
CONSTRUCCIONES GEOMÉTRICAS.
PRODUCIR Y ANALIZAR
CONSTRUCCIONES DE TRIÁNGULOS
CONSIDERANDO LAS PROPIEDADES
INVOLUCRADAS Y LAS CONDICIONES
NECESARIAS Y SUFICIENTES PARA SU
CONSTRUCCIÓN.
PROMOVER EL TRABAJO
COLABORATIVO, LA DISCUSIÓN Y EL
INTERCAMBIO ENTRE PARES, LA
REALIZACIÓN EN CONJUNTO DE LA
PROPUESTA, LA AUTONOMÍA DE LOS
ALUMNOS Y EL ROL DEL DOCENTE
COMO ORIENTADOR Y FACILITADOR DEL
TRABAJO
ESTABLECER VERIFICAR RELACIONES
ENTRE LOS LADOS DE UN TRIÁNGULO
EVALUANDO ALCANCES Y
LIMITACIONES.
OBJETIVOS

11. PLANTEAR Y VALIDAR
HIPÓTESIS A PARTIR
DE LA LECTURA DE
LAS
CONSTRUCCIONES
GEOMÉTRICAS
PROMOVER EL USO DE
LOS EQUIPOS PORTÁTILES
EN EL PROCESO DE
ENSEÑANZA Y
APRENDIZAJE

13. 1.CONSTRUYAN EN HOJA LISA, SIN MEDIR, USANDO SÓLO
REGLA Y COMPÁS; SI ES POSIBLE, TRIÁNGULOS CON LOS
DATOS QUE SE DAN A CONTINUACIÓN:
A)LADOS DE 3CM, 5CM Y 4CM
B)ES EQUILÁTERO Y UNO DE SUS LADOS MIDE 2CM
C)LADOS DE 8CM, 3 CM Y 4CM
D)ES ISÓSCELES Y SUS LADOS CONGRUENTES MIDEN 3CM.

14. 2. ANA QUERÍA CONSTRUIR UN TRIÁNGULO CON LOS
LADOS DE 2,5 CM, 0,7 CM Y 1,4 CM. UTILIZANDO
GEOGEBRA PENSAR Y RESOLVER LA ACTIVIDAD.
3. PROPONÉ A TU COMPAÑERO DE LA DERECHA, LA
CONSTRUCCIÓN DE UN TRIÁNGULO QUE SI SE PUEDA
CONSTRUIR( COMPRUÉBALO UTILIZANDO EL PROGRAMA DE
GEOGEBRA).

15. EL MOMENTO MÁS
DESTACADO DE LA CLASE
FUE LA ACTITUD DE LOS
NIÑOS EN LA RESOLUCIÓN
DEL PROBLEMA CON
GEOGEBRA.
PUDIMOS ANALIZAR LAS
ESTRATEGIAS PARA
RESOLVER CADA
INSTANCIA.

16. PUSIMOS EN JUEGO
ENSAYOS DE RESOLUCIÓN,
IDENTIFICAR ERRORES,
EXPLORAR DINÁMICAMENTE
HASTA CUESTIONARSE SUS
CONOCIMIENTOS ACERCA
DEL SEGMENTO – RECTA.

17. ESTA INSTANCIA A-
DIDÁCTICA DONDE LOS
ALUMNOS SE
ENCUENTRAN CON LOS
PROBLEMAS PARA
RESOLVER PERMITE UN
APRENDIZAJE VALIOSO,
DONDE CADA UNO
PONE EN
CUESTIONAMIENTO LO
ANTERIOR.

18. A ESTO LE AGREGARÍA
LA TAREA CON EL PAR,
ESE INTERCAMBIO
RIQUÍSIMO ENTRE
ELLOS, POSIBILITA
AVANCES
CONCEPTUALES
VALIOSOS.

21. RESPECTO AL MOMENTO DE MAYOR
COMPLICACIÓN, PODRÍA MENCIONAR LA
RAPIDEZ CON QUE DEBÍ LLEVAR A CABO LA
CLASE, PORQUE FUE MUY EXTENSA LA
PRIMERA PARTE Y NO LE DEDIQUÉ TODO EL
TIEMPO NECESARIO A LAS REPREGUNTAS.

23. ESTABLECIMOS
COMPARACIONES
CÓMO SE
SINTIERON CONOCIMIENTOS
ESTRATEGIAS HABILIDADES OBSTRUYEN
POSIBILITAN

24. Y LOS ELEMENTOS DISPONIBLES PARA
CADA CONSTRUCCIÓN ANALIZANDO LAS
DIFERENCIAS Y SIMILITUDES EXISTENTES
ENTRE LAS HERRAMIENTAS DE GEOGEBRA
Y LOS INSTRUMENTOS DE GEOMETRÍA

25. PUESTA EN COMÚN SURGIÓ:
“EN UNA HOJA CUANDO DIBUJAS,
TENÉS QUE TENER MUCHO
CUIDADO, ALGUNAS VECES SE TE
CORRE PARA TODOS LADOS, Y SI
UN COMPAÑERO TE MUEVE EL
CODO Y SE MUEVE LO QUE
HICISTE Y TENÉS QUE VOLVER A
EMPEZAR, EN CAMBIO CON EL
GEOGEBRA HACES CLICK EN
BORRAR Y LISTO, ES MÁS RÁPIDO”
“NOS GUSTÓ
MUCHO”

26. “ES COMPLICADO CUANDO HACÉS EL
PRIMER SEGMENTO PORQUE A PARTIR DE
AHÍ SINO ES EXACTA LA MEDIDA EL
RESTO NO VALE”

27. “ES MÁS EXACTO, PORQUE EN UNA HOJA Y
CON LA REGLA, MARCAR LOS MILÍMETROS
CUESTA MÁS, PERO EN GEOGEBRA TENÉS
QUE ESTAR MÁS ATENTO, PORQUE PONÉS
MAL UN NÚMERO Y TE DA TODO MAL”

28. “SE TRABAJÓ LA PROPIEDAD
DE LOS LADOS DE UN
TRIÁNGULO UTILIZANDO
CIRCUNFERENCIAS Y
PUNTOS DE INTERSECCIÓN”

29. CRÓNICA

30. ¿CUÁLES
FUERON LOS
DESAFÍOS PARA
USTEDES HOY?
(DOCENTE)
“PONER CORRECTAMENTE
LAS UNIDADES”
“QUE NO SE TE
CORRA EL
SEGMENTO”
“QUE ES MUY
SENSIBLE EL
MOVIMIENTO CON EL
MOUSE”

31. EN MI CASO PARA MEJORAR LAS INTERVENCIONES
PODRÍA:
FORTALECER LA
PUESTA EN
COMÚN.
UN MAYOR
INTERCAMBIO ENTRE
LOS NIÑOS. AFIANZAR
MIS RE- PREGUNTAS
SER UN POCO MÁS
INSISTIDORA.
LA ACTIVIDAD UNO
MÁS CORTA.

32. COMO OBSTÁCULO EN MI CASO:
ME CONSIDERO UN
DOCENTE
PRINCIPIANTE CON LA
ENSEÑANZA DE LAS
TIC (GEOGEBRA).
LA CANTIDAD DE
ALUMNOS PRESENTES
PARA LA ACTIVIDAD
LA DISTRIBUCIÓN DE
ELLOS EN EL AULA.

34. COMPARTIR ESTAS
EXPERIENCIAS CON
OTROS COLEGAS Y RE
DIRECCIONARLAS.
INTERCAMBIAR NUEVAS
EXPERIENCIAS Y
PROPUESTAS
DIDÁCTICAS.
ESTA PROPUESTA ME PERMITIÓ:

35. CONTINUAR EN EL
MEJORAMIENTO DE LA
RESOLUCIÓN DE
PROBLEMAS CON
GEOGEBRA.
REFLEXIONAR SOBRE MI
PRÁCTICA
INTERIORIZÁNDOME SOBRE
LAS NUEVAS PERSPECTIVAS
DE LA ENSEÑANZA.

36. LA BÚSQUEDA DE NUEVAS ESTRATEGIAS PARA
QUE LOS ALUMNOS SE SITÚEN ACTIVAMENTE
FRENTE A LA RESOLUCIÓN DE PROBLEMAS.
MI DESAFÍO ES:

37. PONGAN EN JUEGO ESTRATEGIAS, PUEDAN
DISCUTIR,
ANALIZAR,
COMPARAR,
PARA APRENDER NUEVOS CONCEPTOS Y
PODER ASÍ APLICARLOS.

38. DÁNDOLES OPORTUNIDADES PARA EXPRESAR
SU CREATIVIDAD, FOMENTANDO EL TRABAJO
COOPERATIVO.